Tetrahedrite is an abundant and natural sulfosalt mineral, which is considered to be a promising p-type thermoelectric material. Consequently, numerous studies have recently been conducted on synthetic tetrahedrite (Cu₁₂Sb₄S₁₃) [1-3]. Tetrahedrite belongs to the space group, 14¯3m contains 58 atoms per unit cell, and its complex crystal structure results in intrinsically low thermal conductivity [1]. Considering the valences and structural bonding states of Cu, Sb, and S, the composition of the synthetic tetrahedrite can be represented as Cu2IISb10ISb4S12IS^II. Structurally, the rattling of Cu^II atoms, which are located inside the triangular plane of the S atoms, occurs due to the interaction of these atoms with the lone-pair electrons of the Sb atoms, interfering with heat transfer. This leads to low lattice thermal conductivity in tetrahedrites [4-6]. Extensive research has been conducted to improve the thermoelectric properties of tetrahedrites, such as improving the dimensionless figure of merit (ZT) by partial substitution of Cu^II, Sb, or S^II with other elements, specifically, Cu_11.8Co_0.2Sb₄S₁₃, Cu_11.8Ni_0.2Sb₄S₁₃, and Cu_11.6Zn_0.4Sb₄S₁₃ with substituted Co, Ni, and Zn, respectively, on the Cu sites. At 723 K, they achieved ZT values of 0.94, 0.92, and 0.76, respectively [7-9]. Further, Cu₁₂Sb_3.9Bi_0.1Sb₄S₁₃, where Bi is substituted on the Sb site, obtained a ZT value of 0.88 at 723 K [10].

Additional electrons are generated when another transition metal having an oxidation state of +2 or +3 is substituted for the Cu⁺ ion on the Cu^II site. As a result, the charge compensation reduces the carrier (hole) concentration, and the electronic thermal conductivity decreases due to the reduced carrier contribution. In addition, this substitution causes phonon scattering, which in turn leads to low lattice thermal conductivity. Consequently, the dimensionless figure of merit can be improved by doping with transition elements. Tippireddy et al. [11] investigated the density-of-state calculations, magnetic properties, and thermoelectric properties of tetrahedrites, namely: Cu₁₁TMSb₄S₁₃ (TM = Ni, Cu, or Zn) and Cu_11.5TM_0.5Sb₄S₁₃ (TM = Fe, Mn, or Co). As a result, a ZT value of 0.98 and 0.6 was achieved for Cu_11.5Co_0.5Sb₄S₁₃ and Cu_11.5Fe_0.5Sb₄S₁₃, respectively, at 673 K. Lu et al. [2] studied the high-temperature thermoelectric properties of synthetic tetrahedrite by varying the Zn and Fe content in Cu_12-x(Zn/Fe)_xSb₄S₁₃ (x = 1.0 for Zn and x = 0.5 for Fe). As a result, a ZT value of 0.8 was achieved at 720 K for Cu_11.5Fe_0.5Sb₄S₁₃. Nasonova et al. [12] studied the Fe-doped tetrahedrites (Cu_12-xFe_xSb₄S₁₃, where x = 0.0−2.0) using Mössbauer spectroscopy, and proposed an amended model for the Fe³⁺ and Fe²⁺ distributions in the iron-containing tetrahedrite. Weller et al. [13] measured the thermoelectric properties of Cu_12-xFe_xSb₄S₁₃ (x = 1.0−1.5) to observe the ntype behavior at low temperatures.

Since the melting point of Cu is higher than the boiling point of S, the synthesis of tetrahedrite using a conventional melting method requires sophisticated heating, maintenance, and cooling processes. In addition, phase transformation and homogenization are only possible after applying long-term annealing (usually 1-2 weeks) [14, 15]. However, for powder synthesis, mechanical alloying as a solid-state process has several advantages over the melting process with regard to the elimination of certain processes, such as vaporization, phase segregation, and pulverization [16]. In our previous study [17], we determined the optimal processing conditions for the synthesis and consolidation of Cu₁₂Sb₄S₁₃ using mechanical alloying (MA) and hot pressing (HP) processes. A single tetrahedrite phase was obtained in a significantly shorter processing time without post-annealing as compared to the other studies. In this study, the Fe-doped tetrahedrites were prepared by the mechanical alloying and hot pressing (MA-HP) processes, and their thermoelectric properties were examined. When Fe was substituted for Cu, the carrier concentration was reduced due to the added electrons, and thus a high power factor is expected due to the changes in electrical conductivity and Seebeck coefficient. In addition, an improved ZT value is expected due to the decreased thermal conductivity caused by the reduction in lattice contribution, due to phonon scattering and the reduction in carrier contribution due to charge compensation.

Fe-doped tetrahedrites Cu_12-xFe_xSb₄S₁₃ (x = 0.1−0.4) were synthesized by MA. The elemental powders of Cu (99.9% purity, < 45 μm in size, Kojundo Chemical Laboratory Co. Ltd.), Fe (99.9% purity, < 53 μm in size, Kojundo Chemical Laboratory Co. Ltd.), Sb (99.999% purity, < 150 μm in size, Kojundo Chemical Laboratory Co. Ltd.), and S (99.99% purity, < 75 μm in size, Kojundo Chemical Laboratory Co. Ltd.) were weighed to a stoichiometric ratio. Further, 20 g of the mixed powders and 400 g of stainless-steel balls (5 mm in diameter) were placed in a hardened steel jar. After evacuating the jar, Ar gas was injected into the jar and MA was performed at a rotational speed of 350 rpm for 24 h using a planetary mill (Fritsch Pulverisette5). The synthesized mechanically-alloyed powder was charged into a graphite mold having an inner diameter of 10 mm. Subsequently, the HP process was carried out in a vacuum at a temperature of 723 K and a pressure of 70 MPa for 2 h. Detailed conditions of the MA-HP processes have been presented in our previous study [17].

Phases of the HP specimens were confirmed using X-ray diffraction (XRD; Bruker D8-Advance) with Cu Kα radiation (λ = 0.15405 nm). Diffraction patterns were recorded in the θ-2θ mode (2θ = 10−90°) with a step size of 0.02° and a scan speed of 0.4 s/step. Scanning electron microscope (SEM; FEI Quanta400) and energy dispersive spectrometer (EDS; Bruker Quantax200) were used to observe and analyze the microstructures of the sintered specimens. Elemental mapping was conducted to confirm the homogeneous distribution of the constituent elements.

The Hall coefficient, carrier concentration, and mobility of the HP specimens were measured using the van der Pauw method (Keithley 7065); a constant magnetic field of 1 T and a constant current of 100 mA was applied. The Seebeck coefficient and electrical conductivity were measured using the differential temperature method and the DC four-probe method (Ulvac-Riko ZEM-3) in a He atmosphere and at a temperature range from 323 to 723 K. The thermal conductivity was determined using thermal diffusivity, specific heat, and density, measured using the laser flash method (Ulvac-Riko TC-9000H). Finally, the power factor and dimensionless figure of merit were evaluated.

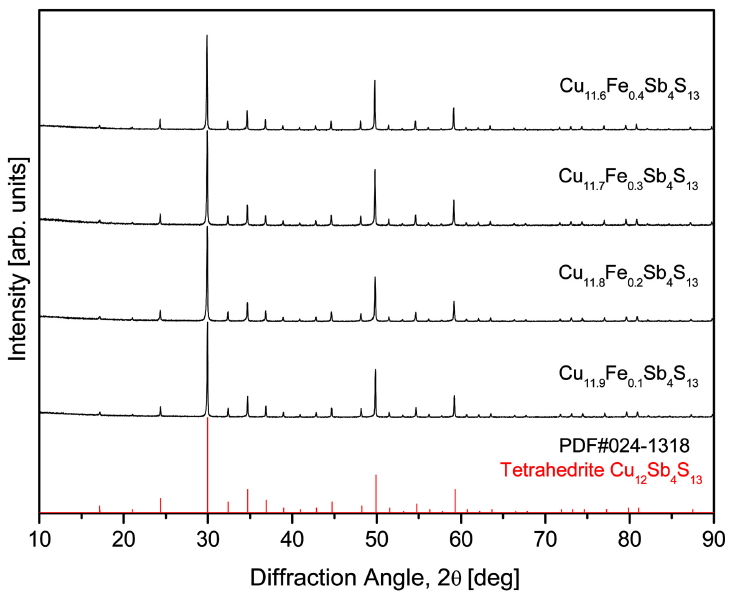
Fig 1 shows the results of XRD analysis according to the Fe content of the sintered Cu_12-xFe_xSb₄S₁₃ specimens. All specimens appeared as a single tetrahedrite phase without secondary phases. Rietveld refinement using the TOPAS program revealed that as the Fe content in Cu_12-xFe_xSb₄S₁₃ increased, the lattice constant increased from 1.0336 nm for x = 0.1 to 1.0350 nm for x = 0.4 (Table 1). Nasonova et al. [12] have also reported that as the Fe content in Cu_12-xFe_xSb₄S₁₃ increased, the lattice constant increased from 1.0320 nm for Cu_11.5Fe_0.5Sb₄S₁₃ to 1.0378 nm for Cu_10.5Fe_1.5Sb₄S₁₃. Tippireddy et al. [11] also found that the lattice constant increased from 1.0320 nm for the synthetic tetrahydride Cu₁₂Sb₄S₁₃ to 1.0330 nm for the Fe-doped tetrahedrite Cu_11.5Fe_0.5Sb₄S₁₃. However, these results are contradictory to the assumption that the lattice constant decreases when smaller Fe³⁺ ions (ionic radius: 49 pm) are substituted at the Cu⁺ sites (ionic radius: 60 pm). Friese et al. [18] suggested that there are ten Cu⁺ and two Cu²⁺ ions (ion radius: 57 pm) in a tetrahedrite structure, and Fe substitution on the Cu site is more stable for the combination of Fe³⁺ and Cu⁺ than the combination of Fe²⁺ and Cu²⁺ [19]. As a result, Cu²⁺ ions are induced to substitute Cu⁺ ions. Consequently, Fe doping results in an increase in the number of Cu⁺ ions, which have a larger ionic radius than Cu²⁺ ions, which in turn results in an increase in the lattice constant.

Fig 2 presents the SEM images of the fractured surfaces of Cu_12-xFe_xSb₄S₁₃. No remarkable differences can be observed in the microstructures based on the Fe content. Highly-dense sintered bodies were obtained with the HP process. Fig 3 shows the EDS elemental maps of Cu_11.8Fe_0.2Sb₄S₁₃ as a representative sample. All the elements were confirmed to be homogeneously distributed. As shown in Table 1, all the specimens have high relative densities greater than 98.8%, without significant differences between the actual and nominal compositions. However, the Fe content is observed to be slightly higher than the nominal composition, which is considered to be due to contamination from the steel jar and steel balls during the MA process. In this study, the solidstate synthesis by MA-HP process suppressed the volatilization of constituent elements, particularly in the case of S.

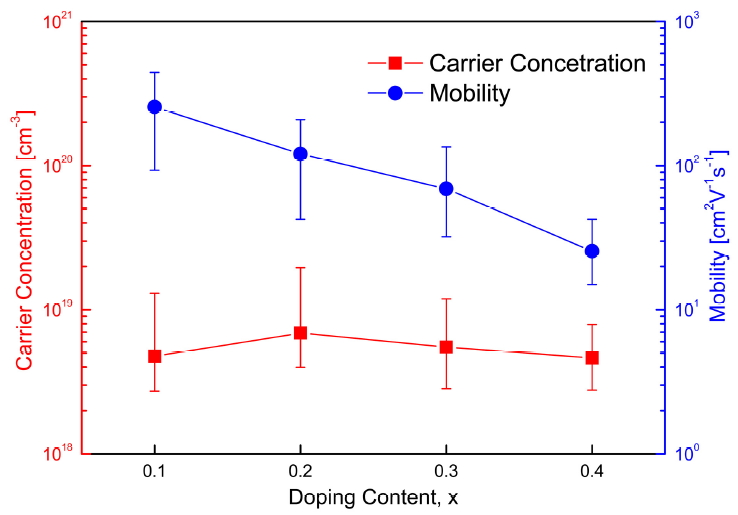
The carrier concentration and mobility of Cu_12-xFe_xSb₄S₁₃ are shown in Fig 4. It can be observed that the mobility tends to decrease with an increase in Fe content, whereas the carrier concentration does not change significantly with Fe content. This was inconsistent with the expectation that the additional electrons would decrease the carrier (hole) concentration following Fe substitution on the Cu site. As the Fe content increased, the mobility decreased due to the increase in charge carrier scattering, which can decrease electrical conductivity. However, the Hall coefficients, measured in this study, exhibited low reliability: the same sample was measured 20 times and extremely different values were obtained. Other researchers have also reported failure when attempting to measure the Hall coefficient of tetrahedrites, as the Hall coefficients were extremely low and close to zero, or extremely different values were obtained when measured again using the same sample [2,11].

The thermoelectric properties of Cu_12-xFe_xSb₄S₁₃ were measured in the temperature range from 323 to 723 K. Fig 5 shows the temperature dependence of the Seebeck coefficient (α) for Cu_12-xFe_xSb₄S₁₃. Positive Seebeck coefficients were observed in all specimens, suggesting that the major carriers are holes of p-type semiconductors. The Seebeck coefficient of the p-type semiconductor is expressed as α = (8/3)π²k_B²m*Te^-1h⁻²(π/3n)^2/3 (where k_B is the Boltzmann constant, m* is the effective carrier mass, T is the absolute temperature, e is the electronic charge, h is the Planck constant, and n is the carrier concentration) [20]. For the specimens with x = 0.10.3, the Seebeck coefficient increased with an increase in temperature. However, for x = 0.4, the Seebeck coefficient decreased with an increase in temperature. As the temperature increases, the Seebeck coefficient of the p-type semiconductor increases; however, if the temperature exceeds a certain temperature (an intrinsic transition temperature), the carrier concentration increases rapidly, and as a result, the Seebeck coefficient decreases.

Therefore, as the temperature of a p-type semiconductor increases, the Seebeck coefficient decreases after achieving a peak value at a specific temperature. In this study, the intrinsic transition occurred at temperatures above 723 K for x = 0.1−0.2 and at 623 K for x = 0.3. However, for x = 0.4, the intrinsic transition had already occurred at temperatures below 323 K. The intrinsic transition temperature is closely related to the bandgap energy, Fermi level, and carrier concentration.

At costant temperature, the Seebeck coefficient increased with an increase in the Fe content. For instance, the value increased from 179 μVK^-1 for Cu_11.9Fe_0.1Sb₄S₁₃ to 224 μVK^-1 for Cu_11.6Fe_0.4Sb₄S₁₃ at 723 K. In this study, Cu_11.6Fe_0.4Sb₄S₁₃ exhibited the highest Seebeck coefficient values of 258–224 μVK^-1 over a temperature range of 323 to 723 K. The increase in the Seebeck coefficients of tetrahedrites, caused by the transition elements substituted on the Cu sites, have been previously reported. Tippireddy et al. [11] obtained the Seebeck coefficient value of 130 μVK^-1 for an undoped tetrahedrite Cu₁₂Sb₄S₁₃ at 673 K. However, after doping with various transition elements (Mn, Fe, Co, Ni, and Zn), higher Seebeck coefficient values were obtained, such as 170 μVK^-1 for Cu_11.5Fe_0.5Sb₄S₁₃ and 215 μVK^-1 for Cu₁₁ZnSb₄S₁₃ at 673 K. Heo et al. [21] also found that the Seebeck coefficient was as low as 74 μVK^-1 for the undoped tetrahedrite Cu₁₂Sb₄S₁₃ at 325 K, but it increased to 170 μVK^-1 for Cu₁₀Fe₂Sb₄S₁₃ and 253 μVK^-1 for Cu₁₀Zn₂Sb₄S₁₃ at 325 K. These high Seebeck coefficients were attributed to the decrease in the carrier (hole) concentration, because the divalent or trivalent transition elements were substituted on the Cu⁺ sites.

Figure 6 presents the temperature dependence of the electrical conductivity (σ) in Cu_12-xFe_xSb₄S₁₃. The electrical conductivity increased with an increase in temperature, and its temperature dependence significantlly increased as the Fe content increased. This indicated that the Fe-doped tetrahedrites behaved as non-degenerate semiconductors. Tippireddy et al. [11] reported that the electrical resistivity of Cu_11.5Fe_0.5Sb₄S₁₃ decreased (i.e., the electrical conductivity increased) with an increase in temperature. Weller et al. [13] also discovered similar results for Cu_12-xFe_xSb₄S₁₃ (x = 1.0, 1.3, and 1.5). The electrical conductivity at a constant temperature decreased with an increase in Fe content, which can be attributed to the effect of charge compensation due to Fe doping [17,21].

In this study, the highest electrical conductivity value of (1.9−2.6) × 10⁴ Sm^-1 was obtained for Cu_11.9Fe_0.1Sb₄S₁₃, while the lowest electrical conductivity value of (1.9–9.9) × 10³ Sm^-1 was obtained for Cu_11.6Fe_0.4Sb₄S₁₃, at temperatures ranging from 323 to 723 K,

Figure 7 shows the temperature dependence of the power factor for Cu_12-xFe_xSb₄S₁₃. The power factor (PF) is expressed as PF = α² σ and increases proportionately with the Seebeck coefficient and the electrical conductivity [22]. Since the carrier concentration affects both Seebeck coefficient (inverseproportionally) and electrical conductivity (proportionally), optimization of the carrier concentration is necessary to obtain high PF values. In this study, the PF increased with an increase in temperature in the measured temperature range, and it decreased as the Fe content increased. The decrease in electrical conductivity due to Fe doping was dominant over the increase in the Seebeck coefficient. Although Cu_11.9Fe_0.1Sb₄S₁₃ exhibited the lowest Seebeck coefficient values, it exhibited the highest PF values of 0.35–0.84 mWm^-1K^-2 in the temperature range of 323 to 723 K, as it exhibited the highest electrical conductivity values. Tippireddy et al. [11] reported a maximum PF of approximately 1.0 mWm^-1K^-2 for Cu_11.5Fe_0.5Sb₄S₁₃ at 673 K.

Figure 8 presents the temperature dependence of the thermal conductivity (κ) for Cu_12-xFe_xSb₄S₁₃. The lattice thermal conductivity (κ_L) from phonon contributions was obtained by subtracting the electronic thermal conductivity (κ_E) of carrier contributions from the total thermal conductivity. Here, κ_E was estimated using the Wiedemann-Franz law (κ_E = LσT, where L is the Lorenz number) [23]. The Lorenz number [10^-8V²K^-2] was calculated using the formula L = 1.5 + exp(-|α|/116) [24]. As shown in Table 1, as the Fe content increased, the Lorenz number decreased from 1.81 × 10^-8 to 1.61 × 10^-8V²K^-2 at room temperature. The electronic thermal conductivity increased with an increase in temperature. However, the total thermal conductivity increased with an increase in temperature and then decreased after obtaining a peak value at 623 K, except for Cu_11.6Fe_0.4Sb₄S₁₃. This was due to the opposition between the increase in electronic thermal conductivity and the minimal changes in the lattice thermal conductivity with an increase in temperature up to 623 K. The electronic thermal conductivity was directly correlated with the electrical conductivity (carrier concentration) and the Lorenz number. Thus, it decreased with increasing Fe content.

In the case of lattice thermal conductivity, Cu_11.6Fe_0.4Sb₄S₁₃ exhibited lower values at temperatures below 523 K due to the enhanced ionized impurity scatterings caused by the dopants. Therefore, Cu_11.6Fe_0.4Sb₄S₁₃ had the lowest total thermal conductivity value of 0.45–0.64 Wm^-1K^-1 for temperatures ranging from 323 to 723 K. Cu_11.5Fe_0.5Sb₄S₁₃, which was studied by Tippireddy et al. [11] exhibited κ = 0.80–1.10 Wm^-1K^-1 in the temperature range of 323 to 623 K, with κ_L = 0.60–0.75 Wm^-1K^-1. In this study, the fine tetrahedrite powders and the absence of the secondary phases in the specimens processed by MA were interpreted to be the reasons for the relatively low values of thermal conductivity.

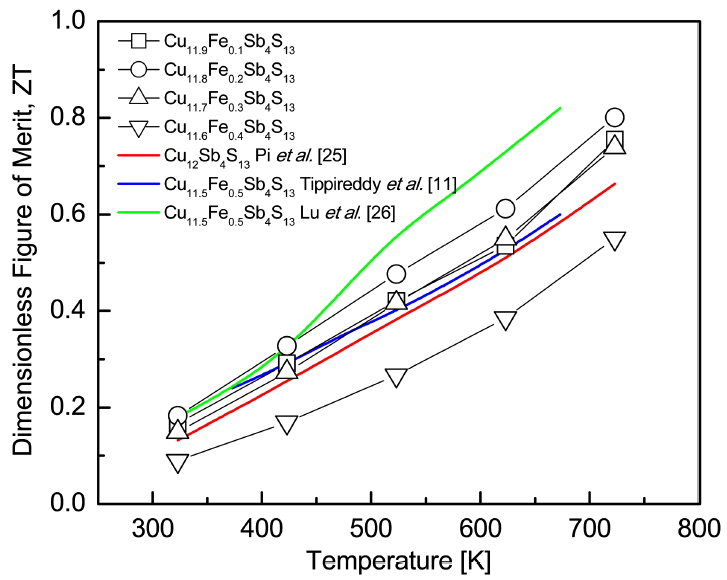
The dimensionless figure of merit (ZT = α²σκ^-1T) values obtained for Cu_12-xFe_xSb₄S₁₃ are shown in Fig 9. As the temperature increased, the ZT values increased. This was attributed to the increase in the power factor and the maintenance of low thermal conductivity. As the Fe content increased, both the PF and thermal conductivity decreased, resulting in the highest ZT value of 0.80 at 723 K for Cu_11.8Fe_0.2Sb₄S₁₃. Pi et al. [25] reported a ZT value of 0.66 at 723 K for the undoped Cu₁₂Sb₄S₁₃ prepared by mechanical alloying and hot pressing with the same processing conditions used in this study. Tippireddy et al. [11] achieved a ZT value of 0.6 at 673 K for Cu_11.5Fe_0.5Sb₄S₁₃, which was fabricated by encapsulated melting and hot pressing process, and Lu et al. [26] obtained a ZT value of 0.8 at 700 K for Cu_11.5Fe_0.5Sb₄S₁₃, synthesized by encapsulated melting and hot pressing process. Tippireddy et al. [11] utilized several days to prepare the tetrahedrite by melting process; initially, it was maintained at 973 K for 3 h, then cooled to 823 K for 30 h, and then further cooled to room temperature, followed by subsequent annealing at 773 K for 30 h. Lu et al. [26] also utilized a very slow and sophisticated melting process, of heating up to 1023 K at a rate of 0.3 K/min, holding for 12 h and then cooling at a rate of 0.5 K/min, followed by subsequent annealing at 723 K for 1 week. However, in this study, the Fe-doped tetrahedrite was successfully synthesized using the MA process for 24 h without subsequent annealing, and it exhibited superior ZT values. Therefore, the MA-HP processes were confirmed to be fast and facile methods of preparing tetrahedrite compounds with high thermoelectric performance.

In this study, Fe-doped tetrahedrites Cu_12-xFe_xSb₄S₁₃ (x = 0.1, 0.2, 0.3, and 0.4) were synthesized by mechanical alloying and sintered by hot pressing. The tetrahedrite compounds comprising relative densities higher than 98.8% were produced without subsequent annealing. The positive values of the Hall and Seebeck coefficients indicated that all the specimens were p-type semiconductors. The electrical conductivity exhibited positive temperature dependence, and its temperature dependence significantly increased as the Fe content increased. The Seebeck coefficient also increased with an increase in temperature, except for Cu_11.6Fe_0.4Sb₄S₁₃. At a given temperature, as the Fe content was increased, more electrons were supplied, which resulted in the decrease in electrical conductivity and the increase in Seebeck coefficient due to charge compensation. The electronic thermal conductivity also decreased in accordance with the trend in electrical conductivity. The total thermal conductivity was also reduced, exhibiting the lowest value for Cu_11.6Fe_0.4Sb₄S₁₃. The power factor decreased with increasing Fe content due to the reduction in electrical conductivity. As a result, a maximum ZT value of 0.80 was achieved at 723 K for Cu_11.8Fe_0.2Sb₄S₁₃. The MA-HP processes were demonstrated to be suitable for fabricating doped tetrahedrites with excellent thermoelectric properties.