1. INTRODUCTION
Understanding the mechanical behavior of polymer materials that exhibit strong time-dependent deformation is required for their reliable design and manufacture [1-5]. Characterizing the relationship between chain structure and viscoelastic deformation is also essential, to control the processing of polymer-based devices. Typically, models used to describe and evaluate viscoelastic deformation in polymers, for example, the spring-and-dashpot model, combine the elastic components of a solid and the viscous components of a fluid [1,2,4,5]. In such viscoelastic models, the coefficients representing the elastic and viscous properties must be measured experimentally.
Uniaxial creep testing (or relaxation testing) and dynamic-mechanical analysis (DMA) under simple tension and compression [5] are widely used to determine ascribed coefficients. However, these methods have limitations, since they have difficulty in evaluating the local characteristics. Conventional uniaxial tests require a specific sample and jig shape to hold and stretch the sample, but at the micro/nano scale, fabricating a specimen and matching jig, and holding the specimen position exactly, is very challenging, especially for flexible organic materials such as rubber. Moreover, the properties determined by conventional tensile testing reflect the average value over the full sample, so local properties cannot be obtained.
For this reason, nanoindentation, which has no limitations on sample size and geometry, has come to the forefront as an attractive method to measure the viscoelastic coefficients [6-8]. Nanoindentation, which measures penetration load and depth, evaluates mechanical properties through the slight penetration of a rigid tip into the sample surface, and thus is almost completely free of limitations on sample preparation [1,2,4,9-12]. Moreover, it can profile local properties [13-16], so that one can investigate the effects of manufacturing processes, and design precise structures.
Here we focus on analyzing the viscoelastic behavior of poly(dimethylsiloxane) (PDMS). The optical transparency and mechanical flexibility of the Si-based polymer PDMS make it of interest as a substrate in flexible electrical systems [6,17,18]. Because these flexible devices undergo large deviations in strain, it is important for reliability to assess the materialŌĆÖs deformation properties. PDMS has high surface energy and shows very good adhesion with metals. A transfer-printing method has recently been introduced that exploits the viscoelasticity and adhesion of PDMS [17,18].
Here we characterize the viscoelastic deformation in PDMS based on nanoindentation curves, at different unloading rates. Several nanoindentation methods use dynamic force with nanoindentation (the so-called dynamic indentation test) [3,19,20], which derives a characteristic viscoelastic value from the loss of energy using a dynamic module. We evaluated the characteristic value with a static module, taking advantage of the perfect elastic recovery of PDMS, which allowed us to make repeated indentations. To describe the viscoelastic behavior in nanoindentation, we correlated the initial unloading stiffness (to be converted into the elastic modulus) with the unloading rate, by combining the representative stress approach and elastic solution in nanoindentation with the Maxwell model, a simple springand-dashpot model. We suggest the viscoelastic coefficient in the relation and discuss their dependency on viscosity and elasticity by using PDMS samples with different viscosity and elasticity. The viscosity and elasticity of the PDMS were controlled by the mixing ratio of PDMS and curing agent. Generally, increasing the proportion of curing agent increases the crosslinking density, which results in an increase in elastic and viscous coefficients [21-23].
2. EXPERIMENTAL
We prepared highly viscous flowing liquid PDMS and a curing agent (Sylgard 184, Dow Corning, Midland, MI). The addition of the curing agent to liquid PDMS transforms it into a flexible solid. The curing agent acts as a branching point and helps form crosslinks, therefore, by controlling the curing agent ratio we can adjust the viscosity and elasticity of the PDMS. Four kinds of PDMS sample were prepared by mixing liquid PDMS and curing agent at four different ratios: 10:0.5, 10:1, 10:2, and 10:3. Vapor in the PDMS-curing agent mixture was removed by putting it in a desiccator for two hours to let the trapped vapor escape. Each mixture was cast in glass-surface molds and cured in vacuum at room temperature for two weeks. Nanoindentation tests were performed using the TriboScope II nanoindenter (Hysitron Inc., Minneapolis, MN) with a Berkovich indenter. To observe the viscoelastic behavior at the initial unloading point, we fixed the maximum indentation load, loading rate and holding time to be 5 mN, 0.05 mN/s and 3 s; the unloading rates were varied from 0.05 to 2 ╬╝N/s.
3. RESULTS AND DISCUSSION
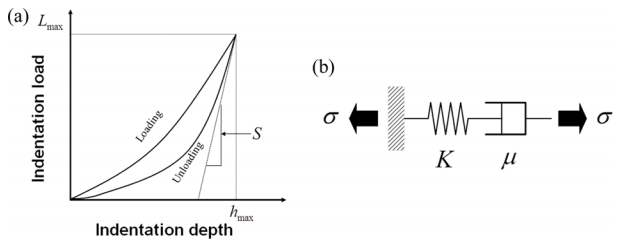
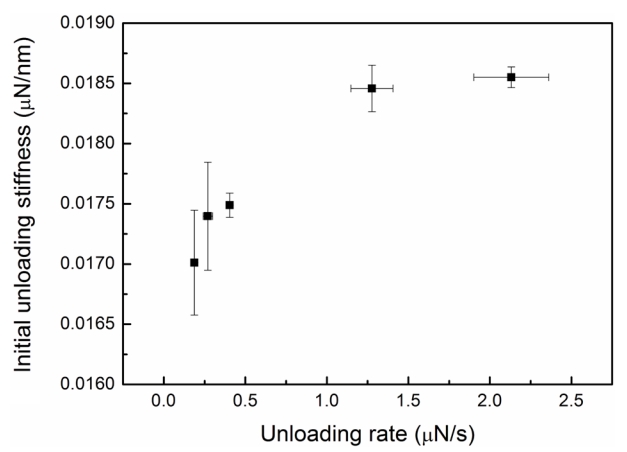
Figure 1 (a) shows a schematic of the indentation loaddepth curve for viscoelastic materials. Previous research [1,2,6] has reported that the indentation load-depth curve shifts as the loading and unloading rate change. The unloading rate affects the variation of initial unloading stiffness, a key parameter in determining the elastic modulus via nanoindentation. Figure 2 shows the relationship between initial unloading stiffness and unloading rate for the PDMS sample with the 10:1 curing agent ratio. The measured initial unloading stiffness was found to depend on the loading rate, indicating a strong viscoelastic response. The initial unloading stiffness converged to a constant as the unloading rate increased, in agreement with previous finite-element analysis (FEA) modeling [1,2] and nanoindentation results [6]. Because viscous deformation requires time, it is almost negligible in high-rate unloading, and thus the converged initial unloading stiffness describes a pure elastic reaction without viscous deformation.
The spring-and-dashpot model in Fig. 1 (b) is widely used to describe the viscoelastic deformation of polymer materials [1,2,4,5] is a well known Maxwell model, which consists of individual springs and dashpots connected in series. In the Maxwell model, the relation between stress and strain is given by
where ╬Ą ╦Ö Žā ╦Ö Žā ╦Ö
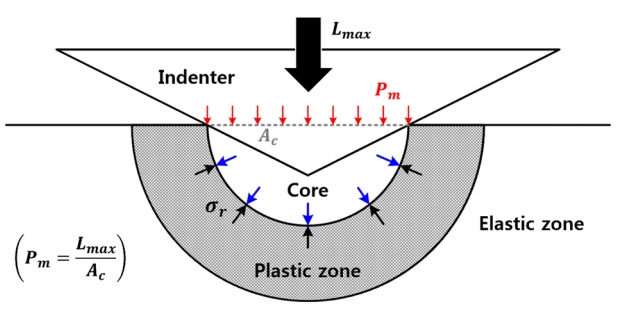
To apply the Maxwell model to nanoindentation, two general concepts in nanoindentation contact mechanics are introduced: the representative stress approach and the elastic solution. In nanoindentation, the representative stress (Žār) is given by the mean pressure (Pm) and the constraint factor (╬©) as
where Lmax is the maximum indentation load and Ac is the contact area (Fig. 3) [10,11,24-26]. The constraint factor was adopted to correlate the radial directional stress under the indenter to the uniform stress in the uniaxial test at the same strain (Fig. 3). That is, through representative stress, the triaxial stress in the indentation test can be matched to the uniaxial stress, which allows us to relate the indentation to the Maxwell model of uniaxial state.
In nanoindentation testing of PDMS, since there is only elastic deformation, it is difficult to obtain an exact constraint factor through the stress distribution of elastic contact, unlike the fully plastic deformation situation, where the constraint factor is defined as 3 [26]. However, because the constraint factor is canceled when deriving Eq. (7) in this study, it is not a problem even if it remains an unknown value. The introduction of representative stress is meaningful in that the triaxial indentation test is associated with the Maxwell model.
The relationship between the elastic modulus (E) and initial unloading stiffness (S) in nanoindentation based on contact mechanics is given by
where Er is the reduced modulus and v is the PoissonŌĆÖs ratio of the sample, and Ei and vi are the elastic modulus and PoissonŌĆÖs ratio of the indenter [12,27,28]. The elastic modulus of the diamond indenter tip is so large compared to that of the PDMS samples that the terms on the right in Eq. (5) can be rewritten as
This equation means that, in a given material, the reduced elastic modulus and the elastic modulus have a linear relationship. The linear relation between the sample elastic modulus and initial unloading stiffness also appears in Eq. (4). In Eq. (2), dŽā/d╬Ą represents the elastic modulus E. Combining Eqs. (2), (3), (4), and (6) yields
Defining 1/KI and 1/╬╝I as ŽĆ ┬Ę ( 1 - v 2 ) / 2 K ŽĆ ┬Ę ( 1 - v 2 ) / 2 ╬╝
At a given indentation depth, the inverse of the initial unloading stiffness, S-1, and the inverse of the indentation unloading rate, (dLmax/dt)-1(which is simply derived from the indentation load-depth curve) are expected to have a linear relationship. The two parameters KI and mI are obtained from the intercept and slope of the linear relationship and are primary parameters describing the viscoelastic behavior in the nanoindentation, like the viscoelastic coefficients in the Maxwell model. It is notable that this relationship is independent of the constraint factor, which is regarded as an unknown parameter. This implies that the stress distribution under the indenter does not affect the viscoelastic behavior of initial unloading stiffness. Finally, we can say that the unloading rate and maximum load at the initial unloading point are critical parameters in viscoelastic unloading behavior.
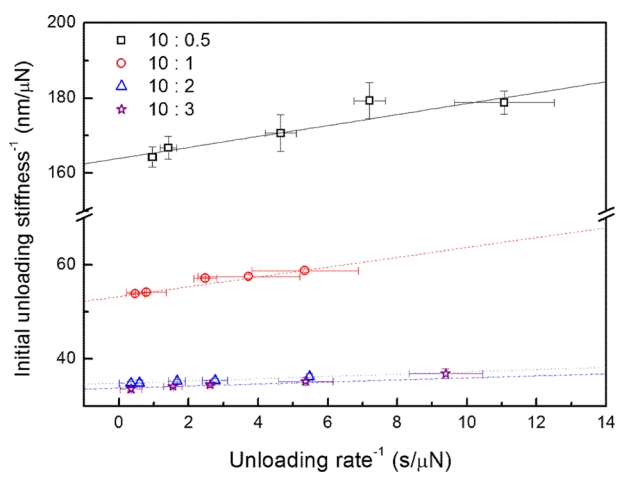
To determine the viscoelastic parameters in nanoindentation, we fitted the experimental data to Eq. (8). Figure 4 shows that the inverse of the unloading rate and the inverse of the initial unloading stiffness have a linear relationship for all curing agent ratios. KI converges to a constant at some ultimate fast unloading rate that is time-independent, like the spring constant in the Maxwell model. In the model developed here, KI is defined as an elastic coefficient. Similarly, mI, which can be determined from the slopes in Fig. 4, corresponds to the viscous dashpot in the Maxwell model, so it is defined as a viscous coefficient.
Polymers can be crosslinked using a curing agent, and this crosslinking density is one of the factors affecting the mechanical properties of polymer materials. An increase in crosslinking density will have the same effect as an increase in molecular mass (M), and will increase the viscosity (╬╝I) as well as the Mark-Houwink relationship:
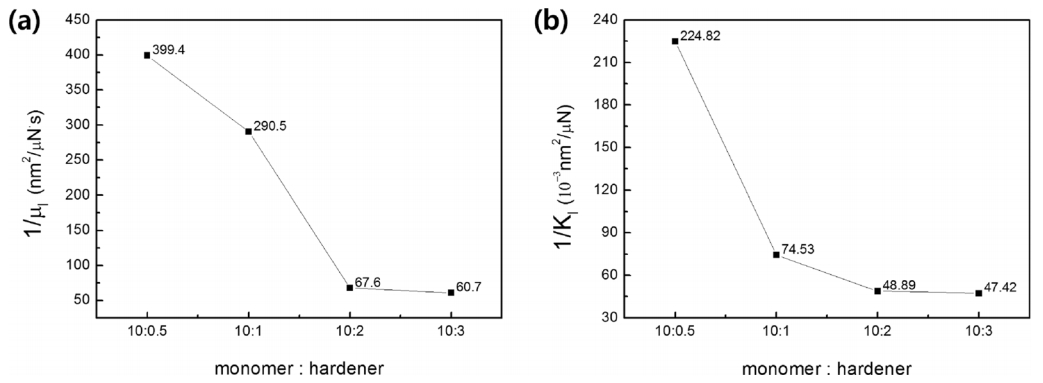
where ╬▒ and ╬▓ are constant for a polymer at a particular temperature [5]. Additional curing agent in a PDMS mixture induces a higher crosslink probability between chains, leading to higher viscosity. Higher viscosity value will cause a lower 1/╬╝I in Eq. (8), which is the slope of the linear relationship between the inverses of unloading rate and initial unloading stiffness. Figure 5 shows the variation in 1/╬╝I as a function of degree of crosslinking density, implies that the viscoelastic coefficients determined by nanoindentation successfully describe the relationship between viscosity and crosslinking density.
The crosslinking density also plays a critical role in the elastic deformation of polymers. More massive chains are harder to deform and condense elastically, so an increase in chain lengths and crosslinking makes a polymer stiffer. This increase in stiffness means a higher spring constant, i.e., a decrease in 1/KI, the y-axis intercept in Eq. (8). Figure 5 (b) shows the decrease in the elastic deformation coefficient with increasing crosslinking density for the PDMS samples. These results imply that the elastic coefficient KI and viscous coefficient ╬╝I determined by nanoindentation describe the viscoelastic deformation behavior of the PDMS in nanoindentation well.
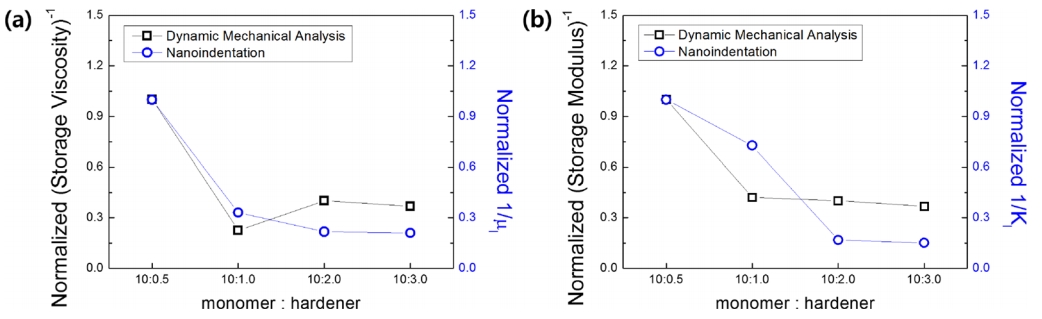
In addition, the DMA test was performed with the same PDMS samples using DMA8000 (Perkin Elmer, Waltham, MA, USA) to confirm that the results for viscosity and elasticity were similar to the indentation results from the conventional test. The storage viscosity and storage modulus were measured from the DMA and the inverse values, and normalized to the inverse values at 10:0.5, in order to compare with the trend in the nanoindentation results. Figure 6 compares the tendency of the viscosity and elasticity obtained by the DMA and nanoindentation based on the mixing ratio (monomer : hardener). Both tests agree that as the ratio of hardener increases, the values tend to decrease. However, it was also confirmed that the tendencies to decrease were different. This may be because the proposed method using nanoindentation is not theoretically sufficient and thus the results of the conventional tests cannot be met. It may result from the difference in testing methods, since nanoindentation evaluates local properties, while DMA evaluates average properties. Further research is needed in this area.
In this study, the viscous and elastic coefficients were obtained using nanoindentation and their tendencies were compared with results obtained from other conventional tests. The changes in viscosity and elasticity with crosslinking density were predicted. This confirmed that the approach employed in this study is reasonable, and if additional studies are complemented, the viscosity and elasticity of the polymer can be quantitatively evaluated using the proposed method.
4. CONCLUSIONS
By applying the indentation representative stress approach and elastic solution to Maxwell model, we found a linear relationship between the inverses of unloading rate and initial unloading stiffness in nanoindentation. We showed a linear relationship experimentally for PDMS samples with different viscosities and elasticities using nanoindentation. It was also found that the viscoelastic unloading depends on the unloading rate and maximum load, rather than the constraint effect at loading. The primary coefficients, KI and ╬╝I, describing the viscoelastic behavior in our model depended on the viscoelastic property of PDMS. In addition, experimentally measured coefficients described well the elastic and viscous behavior expected from the crosslinking density of the PDMS samples.