1. INTRODUCTION
Thermoelectric conversion is an environmentally-friendly energy technique that uses waste heat to generate electrical energy. The energy conversion efficiency of thermoelectric materials is described by the dimensionless figure of merit ZT [1-3]. Skutterudites have attracted attention as thermoelectric materials which operate efficiently at temperatures ranging from 500 K to 900 K. Skutterudites have eight body-centered cubic sublattices with two voids in a unit cell. Atoms (rattlers) which fill these voids cause phonon scattering due to lattice vibrations at unique frequencies. This phonon scattering acts to greatly decrease thermal conductivity, which is an important factor for improving its thermoelectric performance [4-6]. These skutterudites are called ŌĆ£filled skutterudites.ŌĆØ
Both n-type RCo4Sb12 and p-type RFe4Sb12 filled skutterudites have been studied, where R is a filler atom. Co4Sb12 is electronically stable with 72 valence electrons, and n-type RCo4Sb12 has a filling fraction limit (FFL), where the FFL is usually lower than 0.3. High ZT values have been reported for n-type filled skutterudites due to their excellent electrical properties [7,8]. However, Fe4Sb12 has 68 valence electrons and is electronically unstable with four deficient electrons. Thus, it requires excess electrons from filler atoms, and as a result the fillers can be incorporated in voids up to FFL = 1. Therefore, p-type RFe4Sb12 has no FFL.
Rare-earth elements are generally used as the fillers, where most have valences of R2+ and R3+. This means charge compensation is required, and it can be implemented by substituting Co or Ni for Fe, e.g., RzFe4-x(Co/Ni)xSb12. P-type skutterudites require charge compensation for phase stabilization and improved thermoelectric performance. However, the carrier (hole) concentration needs to be optimized through charge compensation and partial filling, resulting in relatively low ZT values compared with n-type skutterudites. For this reason, many studies have focused on improving the thermoelectric performance of p-type skutterudites with methods including void filling (double filling), substitution, mechanical deformation, particle size control, and so on [9-11].
Each filler atom has a unique mass and oscillation frequency [7]. Enhanced phonon scattering can be expected due to differences in mass and resonance frequency when two or more filler elements are used. This is called double or multiple filling. Partially double-filled p-type skutterudites (Ce1-zYbz)0.8Fe4-xCoxSb12 were prepared in this study. The phase, microstructure, charge transport, and thermoelectric properties were evaluated according to the filling ratio and amount of charge compensation.
2. EXPERIMENTS
Ce/Yb-partially-filled and Co-substituted (Ce1-zYbz)0.8Fe4-xCoxSb12 (z = 0.25, 0.75 and x = 0, 0.5, 1.0) skutterudites were synthesized by encapsulated melting. Ce (purity 99.9%), Yb (purity 99.9%), Fe (purity 99.95%), Co (purity 99.95%), and Sb (purity 99.999%) were weighed and mixed in a carbon-coated quartz tube. The vacuum-sealed ampoule was heated (melted) at 1323 K for 10 h and then water-cooled. The ingot was vacuum-sealed again and heat-treated at 873 K for 24 h in order to enforce homogenization. The obtained ingot was pulverized into a powder with particle sizes of less than 75 ╬╝m. The powder was then charged into a graphite mold with an inner diameter of 10 mm and sintered by hot pressing under a pressure of 70 MPa at 873 K for 1 h. X-ray diffraction (XRD: Bruker, D8-Advance) was used for phase analysis and to determine the lattice constants of the sintered specimen. The microstructure of the sintered body was examined by scanning electron microscopy (SEM: FEI, Quanta400). The chemical composition was analyzed by energy dispersive spectroscopy (EDS: Bruker, Quantax200).
The Hall coefficient (RH) was measured using the van der Pauw method (Keithley 7065) in order to analyze the charge transport parameters:
where VH is the potential difference between Hall probes, t is the thickness of the specimen, I is the applied electric current, and B is the applied magnetic field. The carrier concentration (n) can be obtained from Eq. 2:
where e is the electron charge, ╬╝ is the carrier mobility, Žā is the electrical conductivity, and kH is the degree of degeneration, which depends on the carrier scattering factor. In this study, a magnetic field of 1 T and a direct current of 50 mA were applied at room temperature, assuming kH = 1 as is the case for a single parabolic band. The Seebeck coefficient (╬▒), electrical conductivity (Žā), and thermal conductivity (╬║) were measured at temperatures ranging from 323 K to 823 K. The Seebeck coefficient was measured using the temperature differential method (Ulvac-Riko, ZEM-3), where the Seebeck voltage generated by a temperature gradient is measured between both ends of the specimen. The electrical conductivity was measured using the DC four-probe method (Ulvac-Riko, ZEM-3). The thermal diffusivity (D), specific heat (cp), and density (d) were measured for each sample using the laser flash method (Ulvac-Riko, TC 9000H), and the thermal conductivity was calculated using Eq. 3:
3. RESULTS AND DISCUSSION
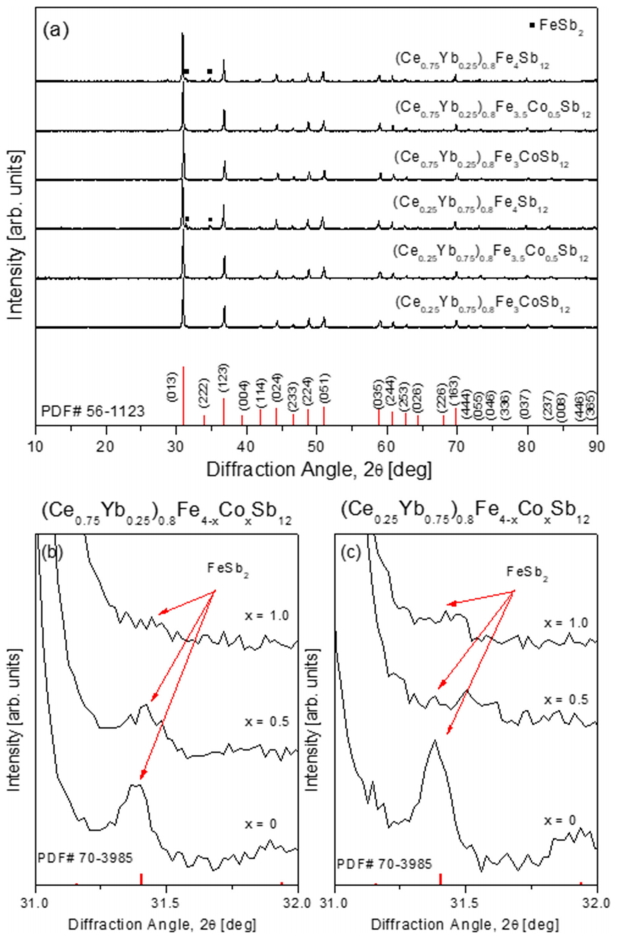
Figure 1 shows the XRD patterns of the (Ce1-zYbz)0.8Fe4-xCoxSb12 skutterudites. The diffraction peaks from all specimens were consistent with the standard diffraction data for the skutterudite phase (PDF# 56-1123, space group: Im ), indicating that Ce and Yb filled the voids in the skutterudite lattice, and the skutterudite phase was successfully synthesized and stabilized. However, for the (Ce1-zYbz)0.8Fe4Sb12 specimens without Co substitution, the marcasite (FeSb2) phase (PDF# 70-3985, space group: Pnnm) was detected in addition to the skutterudite phase. The fraction of marcasite significantly decreased with increasing Co concentration, as shown in Figs 1(b) and 1(c). As the contents of filled Ce and substituted Co increased, the diffraction peaks shifted to higher angles, indicating the lattice constant decreased. This resulted from differences in the ionic radii; the ionic radii of Yb (116 pm) and Fe (75-92 pm) are larger than those of Ce (102 pm) and Co (69-75 pm) [12]. Consequently, the lattice constants decreased as the content of Ce and Co increased. The calculated lattice constants are listed in Table 1.
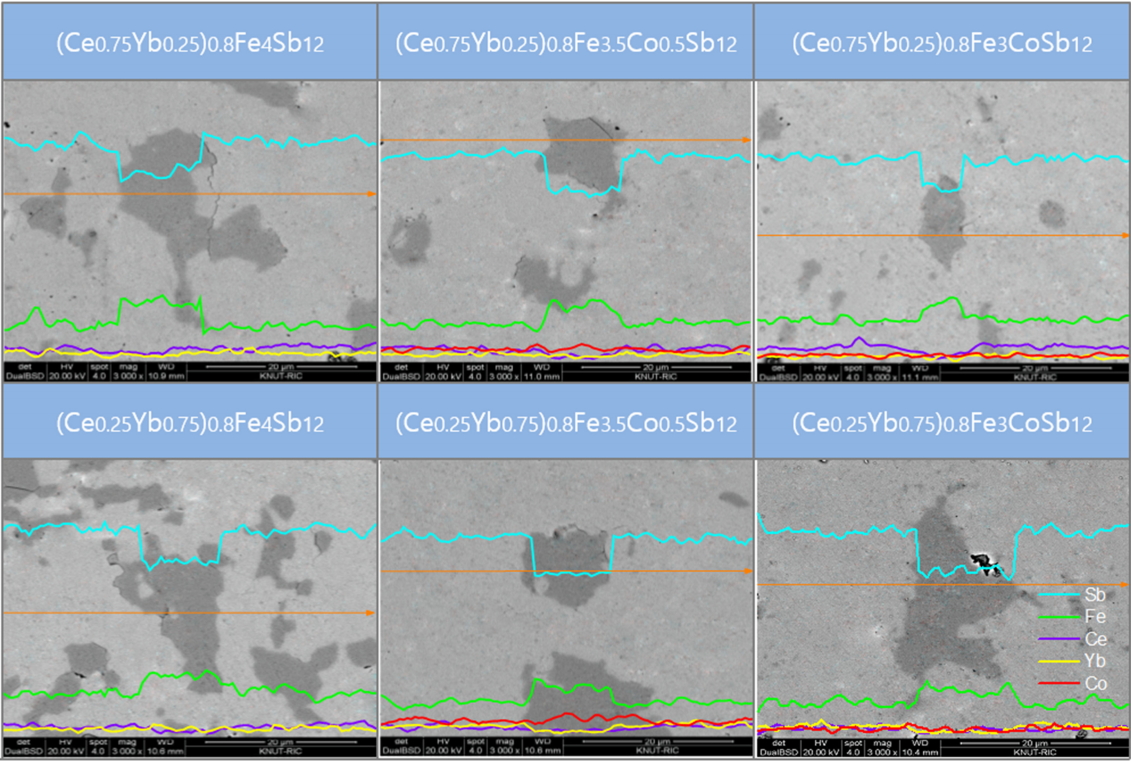
Figure 2 shows SEM images and EDS line scans of (Ce1-zYbz)0.8Fe4-xCoxSb12. The matrix phase corresponds to the skutterudite, but a secondary phase was also observed, which is enlarged in Fig 2. From the EDS analysis, the secondary phase was estimated to be the marcasite FeSb2 phase, which is consistent with the XRD results. The partially-filled (Ce1-zYbz)0.8Fe4Sb12 without Co charge compensation generated a large number of secondary phases. However, as the content of Co increased, the number of secondary phases considerably decreased, which implies that the skutterudite phase could be stabilized by Co substitution. In this study, rare-earth antimonides such as CeSb2, YbSb2, and (Ce,Yb)Sb2 were not produced, all of which one would expect to see from partial filling.
Table 1 shows the chemical composition, relative density, lattice constant, and charge transport properties of (Ce1-zYbz)0.8Fe4-xCoxSb12 at room temperature. The actual composition for each material was similar to the nominal composition, confirming that volatilization and oxidation of the constituent elements were suppressed during synthesis and sintering. Sintered bodies with relative densities of 95.1-99.2% were obtained by hot pressing. The calculated relative density values include some errors because only the theoretical density and the sintered density of the pure skutterudite were taken into account without considering the content and theoretical density of the marcasite phase. The Hall coefficient showed positive values for all specimens, which meant that holes acted as the major carriers, i.e., the materials are p-type. The carrier concentration was lower as the amount of filled Ce and substituted Co increased. Due to the different valences of Ce3+/4+ and Yb2+/3+, Ce provided more excess electrons than Yb, thus the carrier (hole) concentration decreased. On the other hand, because the electronic configurations of Fe and Co are [Ar]3d64s2 and [Ar]3d74s2, respectively, while Co substitution decreased the carrier concentration, the skutterudite phase could be stabilized by the generation of surplus electrons [13,14]. The carrier mobility changed with the filling ratio of Ce/Yb and the concentration of substituted Co, showing the opposite tendency as the carrier concentration. This is a typical effect that results from carrier scatterings.
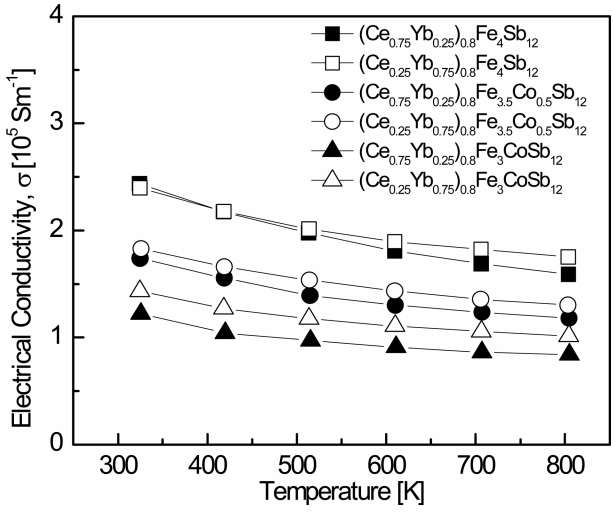
Figure 3 shows the temperature dependence of the electrical conductivity for (Ce1-zYbz)0.8Fe4-xCoxSb12. The electrical conductivity slightly decreased as the temperature increased, indicating that all specimens were degenerate semiconductors. (Ce0.75Yb0.25)0.8Fe4Sb12 showed the highest electrical conductivity of 2.44 ├Ś 105 Sm-1 at 323 K, and (Ce0.75Yb0.25)0.8Fe3CoSb12 showed the lowest electrical conductivity of 8.40 ├Ś 104 Sm-1 at 823 K. At a constant temperature, the electrical conductivity decreased with increased Ce filling and Co substitution. As shown in Table 1, the electric conductivity decreased due to differences in the valences of Ce and Yb and to the reduction in carrier concentration caused by the Co charge compensation.
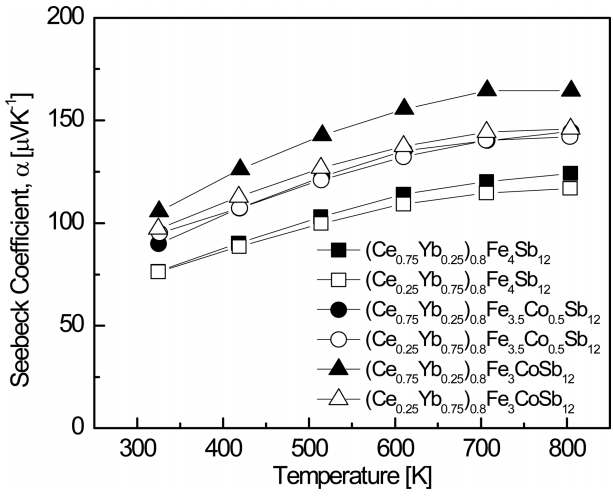
Figure 4 shows the temperature dependence of the Seebeck coefficient for (Ce1-zYbz)0.8Fe4-xCoxSb12. The carrier concentration decreases as the temperature increases, and the Seebeck coefficient increases:
where kB is the Boltzmann constant, m* is the carrier effective mass, and h is the Planck constant. In this study, the Seebeck coefficient increased as the temperature rose, but it began to decrease gradually above a certain temperature. This was because intrinsic transitions occurred at temperatures higher than a specific temperature, and as a results, the carrier concentration increased rapidly. As the amount of filled Ce and substituted Co increased, the Seebeck coefficient increased because the number of electrons provided to the matrix increased due to the valence differences and charge compensation. Seebeck coefficients have positive values, just like Hall coefficients [15]. (Ce0.75Yb0.25)0.8Fe3CoSb12 showed the highest values of 105.6 ╬╝V K-1 at 323 K and 164.5 ╬╝V K-1 at 723 K.
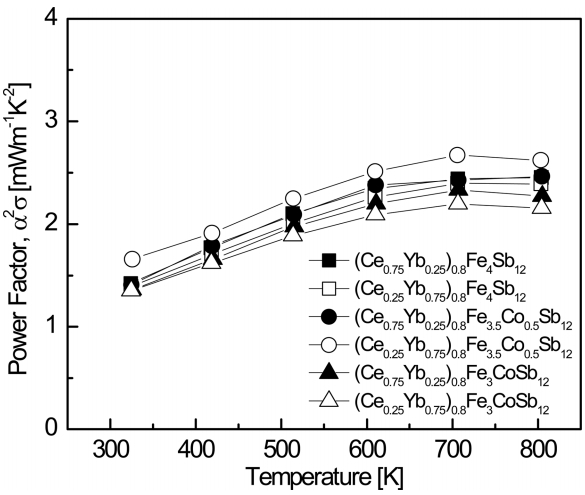
Figure 5 shows the temperature dependence of the power factor (PF) for (Ce1-zYbz)0.8Fe4-xCoxSb12. The PF reached a maximum at temperatures ranging from 723 K to 823 K. This was attributed to the reduced rate of change in the electrical conductivity with temperature rise and to the saturated Seebeck coefficient caused by intrinsic transitions, as shown in Figs 3 and 4. The PF increased with increasing Yb content, and the Co-substituted specimen with x = 0.5 showed the highest PF value. This was because both the electrical conductivity and Seebeck coefficient depend on carrier concentration, as shown in Eqs. 2 and 6. As a result, (Ce0.25Yb0.75)0.8Fe3.5Co0.5Sb12 exhibited a maximum PF of 1.67 mW m-1 K-2 at 323 K and 2.67 mW m-1 K-2 at 723 K.
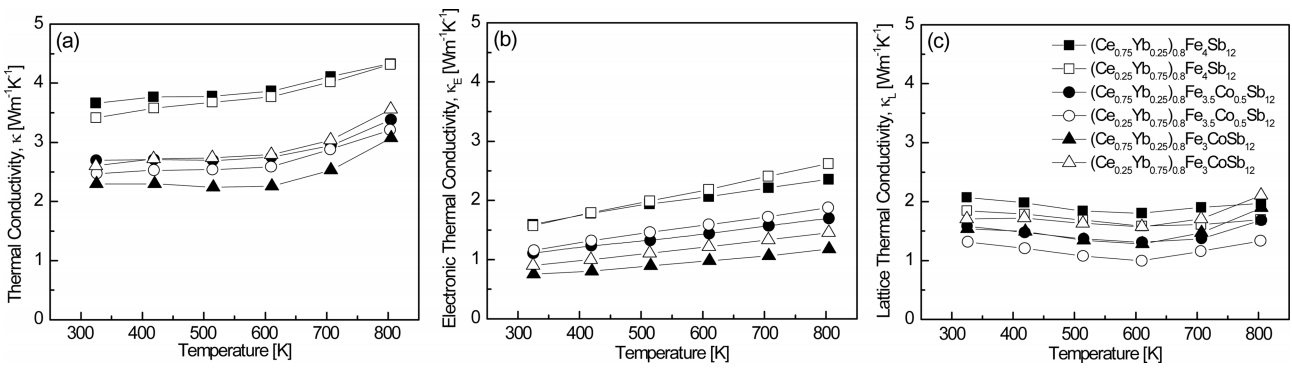
Figure 6 shows the temperature dependence of the thermal conductivity for (Ce1-zYbz)0.8Fe4-xCoxSb12. The thermal conductivity is the sum of the electronic thermal conductivity (╬║E) and lattice thermal conductivity (╬║L):
where the electronic thermal conductivity can be calculated using the Wiedemann-Franz law (╬║E = LŽāT) and the Lorenz constant (L) was assumed to be 2.00 10-8 V2 K-2 in this study. The total thermal conductivity decreased with increasing temperature and then increased again at 623 K, which was due to bipolar conduction. The electronic thermal conductivity increased with increasing temperature, although it had lower values with increasing Ce and Co contents as these additives reduced carrier concentration. (Ce0.75Yb0.25)0.8Fe3CoSb12 exhibited the lowest electronic thermal conductivity of ╬║E = 0.76ŌĆō1.18 W m-1 K-1 at temperatures ranging from 323 K to 823 K. (Ce0.25Yb0.75)0.8Fe3.5Co0.5Sb12 showed the lowest lattice thermal conductivity of ╬║L = 1.31ŌĆō1.33 W m-1 K-1 at temperatures ranging from 323 K to 823 K, which were relatively low values due to enhanced phonon scattering caused by the difference in resonance frequency (Ce: 73 cm-1 and Yb: 52 cm-1) [16]. As a result, (Ce0.75Yb0.25)0.8Fe3CoSb12 showed the lowest total thermal conductivity of ╬║ = 2.30ŌĆō3.07 W m-1 K-1 at temperatures ranging from 323 K to 823 K.
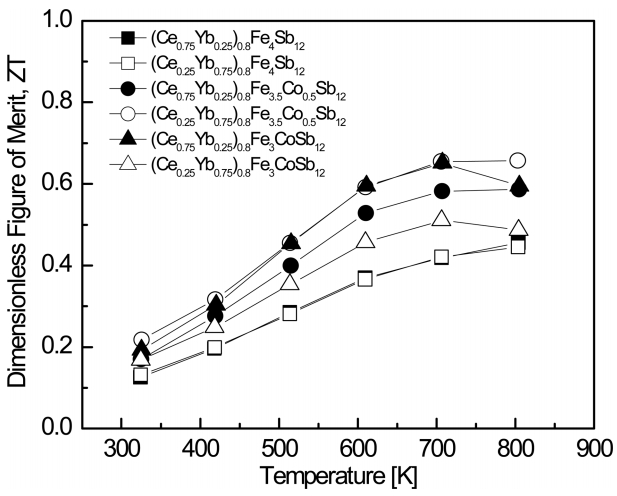
Figure 7 shows the temperature dependence of the dimensionless figure of merit (ZT) for (Ce1-zYbz)0.8Fe4-xCoxSb12. As the temperature increased, the ZT value increased and reached a maximum value at a certain temperature. As shown in Eq. 5, this was attributed to the decreased Seebeck coefficient (the power factor) due to intrinsic transitions and the increased thermal conductivity due to bipolar conduction. As the content of Co increased, the temperature corresponding to the peak ZT value shifted to lower temperatures. In the case of (Ce0.75Yb0.25)0.8Fe4-xCoxSb12 at a constant temperature, the ZT value increased with increasing Co substitution. This was due to the lower thermal conductivity. However, in the case of (Ce0.25Yb0.75)0.8Fe4-xCoxSb12, the Co-substituted specimen with x = 0.5 exhibited the highest ZT value, which was due to the high PF value. As a result, (Ce0.25Yb0.75)0.8Fe3.5Co0.5Sb12 exhibited a maximum ZT value of 0.66 at 823 K. However, this value was lower than the ZT values of Ce/Yb-fullydouble-filled skutterudites; Ballikaya et al. [17] reported ZT = 1.0 at 750 K for Ce0.5Yb0.5Fe3.25Co0.75Sb12, and Joo et al. [18] reported ZT = 0.87 at 723 K for Ce0.75Yb0.25Fe3.5Co0.5Sb12. In this study, partial double filling with Ce/Yb inhibited the formation of secondary phases (Ce,Yb)Sb12, but it was not effective at improving the thermoelectric performance.
4. CONCLUSIONS
Skutterudites with desirable thermoelectric performance at intermediate and high temperatures were prepared. Charge transport and thermoelectric properties were examined with varying levels of partial double filling and charge compensation. (Ce1-zYbz)0.8Fe4-xCoxSb12 (z = 0.25, 0.75 and x = 0, 0.5, 1.0) skutterudites were synthesized by encapsulated melting and annealing, and were subsequently consolidated by hot pressing. The main phase in all specimens was the skutterudite phase, but a small amount of marcasite was detected, which was inhibited by Co substitution. (Ce,Yb)Sb12 phases were not formed due to partial filling. The lattice constants decreased with increasing Ce and Co contents. The electrical conductivity showed a negative temperature dependence, as is the case in degenerate semiconductors. Positive Hall and Seebeck coefficients were obtained, indicating p-type conductivity. As the amount of Ce filling and Co substitution increased, the electrical conductivity decreased due to decreased carrier concentration, and the thermal conductivity decreased due to reduced phonon scattering and electronic thermal conductivity. As a result, (Ce0.25Yb0.75)0.8Fe3.5Co0.5Sb12 exhibited the greatest dimensionless figure of merit (ZT = 0.66 at 823 K).