1. INTRODUCTION
Thermoelectric devices convert thermal energy into electrical energy directly and reversibly. The performance of thermoelectric materials is determined by a dimensionless figure of merit, ZT = ╬▒2ŽāT╬║ŌĆō1, where ╬▒ is the Seebeck coefficient, Žā is the electrical conductivity, ╬ż is the absolute temperature, and ╬║ is the thermal conductivity [1]. To obtain higher ZT values, thermoelectric materials should have a high Seebeck coefficient, high electrical conductivity, and low thermal conductivity. However, the Seebeck coefficient and the electrical conductivity have a trade-off relationship with carrier concentration. In addition, it is difficult to control each parameter independently, because the thermal conductivity increases as the electrical conductivity increases [2,3]. The requirements for good thermoelectric performance are described by the phonon-glass and electron-crystal (PGEC) concept proposed by Slack [4]. The conditions for obtaining high ZT values include a complex structure with a large unit cell, strong atomic bonds, large atomic masses, high carrier mobility, narrow bandgap energy, and low thermal conductivity. Skutterudite satisfies these criteria except for the low thermal conductivity condition [4].
Skutterudite has the basic form of 8MX3 (M: transition metal and X: pnicogen element) and two large voids in the unit cell. Thermal conductivity can be reduced by filling heavy atoms (fillers or rattlers) into the voids. The phonon scattering is enhanced by the rattling effect of lattice vibrations in the void. Therefore, the lattice thermal conductivity can be reduced and the thermoelectric performance can be improved [5,6]. Such filled skutterudites have the chemical formula RM4X12 (R: alkali, alkaline-earth, or rare-earth metal). The CoSb3-based n-type filled skutterudite is used in the form RzCo4Sb12 [5-8], and the FeSb3-based p-type filled skutterudite is used in the form RzFe4Sb12 [9-11]. The n-type Co4Sb12 skutterudite is stable with 72 valence electrons, but the p-type Fe4Sb12 skutterudite is unstable because it has only 68 valence electrons. Therefore, excess electrons are required for stabilization [11]. Phase stabilization with the R4+[Fe4Sb12]4- form is possible by filling the void, but most of the elements used as fillers exist as valences of R2+ and R3+. As a result, the valence electrons are absent when filling these elements [12]. Thus, charge compensation is needed, and fulfilled by substituting Co or Ni for the Fe site. In addition, p-type skutterudites show lower thermal conductivities than n-type skutterudites, but owing to their low charge transport and electrical properties, they exhibit lower ZT values than those of n-type skutterudites [13]. Therefore, it is necessary to improve the thermoelectric performance of p-type skutterudites.
Filling the voids in a skutterudite structure is a very effective method of reducing the lattice thermal conductivity, because each filler atom has a specific resonant frequency and acts as a phonon scattering center [5,8,14,15]. If two or more kinds of rare-earth elements with heavier atomic masses are filled, the lattice thermal conductivity can be further reduced owing to the broader spectrum of phonon frequencies [5,6,9]. Thus, double- or multiple-filling can cause more phonon scattering, resulting in improved thermoelectric performance with a lower lattice thermal conductivity [6,15-17]. Recently, some studies have reported that p-type skutterudites cannot be completely filled when the charge compensation is performed by substituting Co or Ni at the Fe site [18-20]. In our previous study, La/Pr double-filled and Co-substituted skutterudites exhibited (La,Pr)Sb2 secondary phases because the La/Pr double filling exceeded the filling fraction limit (FFL) [21]. In this study, La/Pr-partiallydouble-filled and Co-substituted (La1ŌłÆzPrz)yFe4ŌłÆxCoxSb12 were prepared, and their thermoelectric and charge transport properties were examined.
2. EXPERIMENTAL PROCEDURE
La (purity 99.9%, Kojundo), Pr (purity 99.9%, Kojundo), Fe (purity 99.95%, Cerac), Co (purity 99.95%, Alfa Aesar), and Sb (purity 99.999%, LTS) were combined according to the stoichiometry of (La1ŌłÆzPrz)0.8Fe4-xCoxSb12, melted at 1323 K for 10 h using encapsulated melting, and then quenched in water. The ingot was annealed at 873 K for 24 h in an evacuated quartz ampoule, and ground to powder with particle diameters less than 75 ╬╝m. The synthesized powder was charged into a graphite mold with an inner diameter of 10 mm and hot pressed with 70 MPa of applied pressure at 898 K for 1 h in a vacuum.
Phase and lattice constants were analyzed by X-ray diffraction (XRD: Bruker, D8 Advance) with Cu K╬▒ (40 kV and 30 mA) radiation. Diffraction peaks were measured in qŌĆō2q mode (2╬Ė = 10┬░ to 90┬░) with a step size of 0.02┬░, a scan speed of 0.4 s/step, and a wavelength of 0.15405 nm. The microstructures were observed by scanning electron microscopy (SEM, FEI, Quanta 400), and the chemical compositions were analyzed by energy-dispersive spectroscopy (EDS: Bruker, Quantax 200). The sintered specimens were cut into rectangular pieces with dimensions of 3 ├Ś 3 ├Ś 9 mm3 to measure both the Seebeck coefficient (╬▒) and the electrical conductivity (Žā), which were measured by a DC 4-probe method with the ZEM-3 (Ulvac-Riko) equipment. The hotpressed specimens were also cut into discs with dimensions of 10 (diameter) ├Ś 1 mm2 (thickness) to measure both the thermal conductivity (╬║) and the Hall effect. The thermal conductivity (╬║ = Dcpd) was evaluated by measuring the thermal diffusivity (D), specific heat (cp), and density (d) using the laser flash method with the TC-9000H (Ulvac-Riko) equipment. The Hall coefficient, carrier concentration, and mobility were measured using a Keithley 7065 system at room temperature with a constant magnetic field (1 T) and current (50 mA). The power factor (PF ╬▒2= Žā) and the dimensionless figure of merit (ZT = ╬▒2ŽāT╬║ ŌĆō1) were evaluated using the measured Seebeck coefficient and electrical conductivity and the calculated thermal conductivity.
3. RESULTS AND DISCUSSION
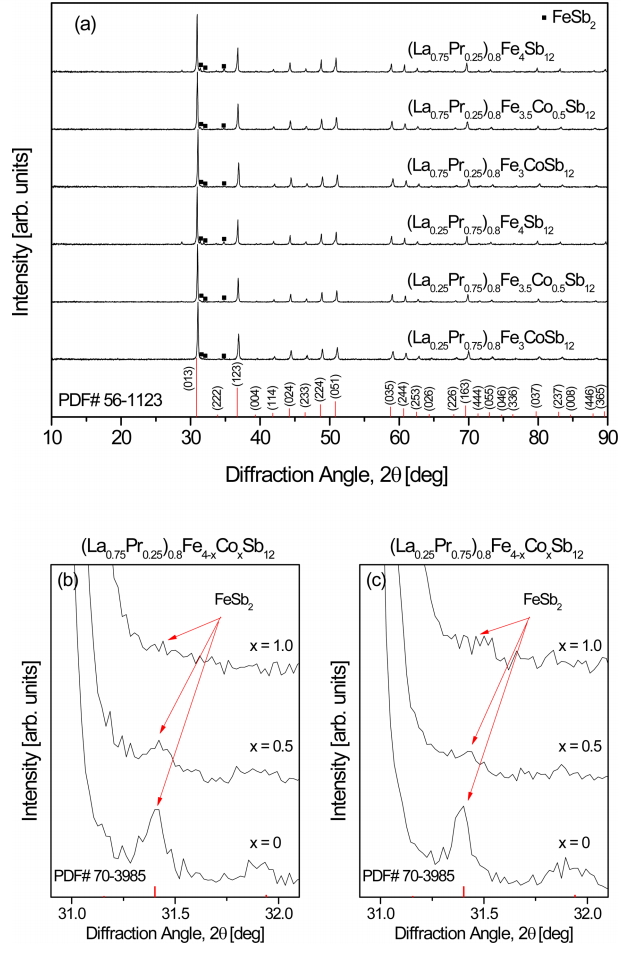
Figure 1 shows the XRD patterns of (La1ŌłÆzPrz)0.8Fe4ŌłÆxCoxSb12. The diffraction peaks of all specimens correspond to the standard data for the skutterudite phase (PDF# 56-1123, space group: Im3 ┬»
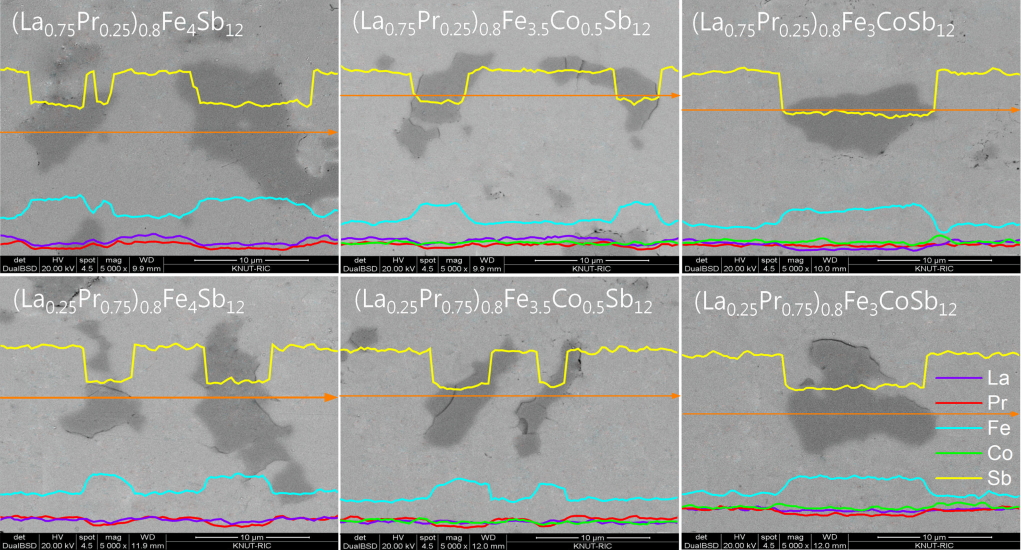
Figure 2 shows the SEM images and EDS line scans of (La1ŌłÆzPrz)0.8Fe4ŌłÆxCoxSb12. The FeSb2 phase (dark region) was formed with the skutterudite phase (bright region), but the formation of the FeSb2 phase was inhibited with increasing Co content. In our previous study, (La,Pr)Sb2 phases were observed in the fully-filled La1-zPrzFe4-xCoxSb12 specimens, exceeding the FFL [21]. However, in the present study, the partially-filled (La1ŌłÆzPrz)0.8Fe4-xCoxSb12 skutterudites did not produce (La,Pr)Sb2 secondary phases. Therefore, it was confirmed that the (La,Pr)Sb2 phase was not formed when the partial filling did not exceed the FFL.
Table 1 shows the chemical compositions, relative densities, lattice constants, and charge transport properties of (La1ŌłÆzPrz)0.8Fe4ŌłÆxCoxSb12. The actual compositions showed no significant differences from the nominal compositions after the synthesis, annealing, and sintering, thus the processes and conditions of sample preparation were reasonable. All specimens showed a relative density higher than 98.5% of the theoretical density. The calculated lattice constants ranged from 0.9117 to 0.9133 nm according to the La/Pr filling ratio and Co substitution amount. Because the atomic radius of Co (0.167 nm) is smaller than Fe (0.172 nm), the lattice constant decreased with increasing Co substitution. In addition, because Pr (0.133 nm) is smaller than La (0.136 nm), the lattice constant further decreased with increasing Pr filling [22,23]. All specimens showed positive Hall coefficients, indicating p-type conduction by the majority charge carriers of holes. The carrier concentrations ranged from 1.08 ├Ś 1021 to 3.59 ├Ś 1021 cmŌłÆ3, which decreased with increasing Co and Pr contents. This decrease in the carrier concentration was due to the charge compensation induced by substituting Co for Fe and to the differences in valence states of La3+ and PR3+/4+. The carrier mobility varied inversely with the carrier concentration, which was a general behavior due to ionized impurity scattering.
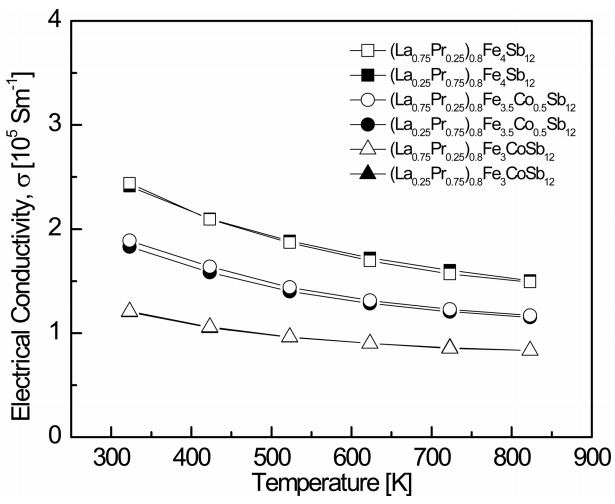
Figure 3 shows the temperature dependence of the electrical conductivity for (La1ŌłÆzPrz)0.8Fe4ŌłÆxCoxSb12. The electrical conductivity decreased with increasing temperature, indicating that the specimens were degenerate semiconductors. The electrical conductivity decreased as the content of Co increased at constant temperature. As shown in Table 1, this was due to the decreased carrier concentration caused by charge compensation. The change in the electrical conductivity with the La/Pr filling ratio was not significant. The electrical conductivities ranged from 1.20 ├Ś 105 to 2.44 ├Ś 105 Sm-1 at 323 K, while the fully-filled specimens showed electrical conductivities from 1.26 ├Ś 105 to 2.33 ├Ś 105 Sm-1 at 323 K [21]. The (La0.75Pr0.25)0.8Fe4Sb12 sample showed the highest electrical conductivity of 2.44 ├Ś 105 Sm-1 at 323 K.
Figure 3 shows the temperature dependence of the Seebeck coefficient for (La1ŌłÆzPrz)0.8Fe4ŌłÆxCoxSb12. All specimens showed positive Seebeck coefficients, reconfirming p-type conduction. The Seebeck coefficient increased with increasing temperature, and it further increased with increasing Co and Pr contents. The Seebeck coefficient can be expressed as ╬▒ = (8 Ōüä 3)ŽĆ 2 kB2mŌłŚTe ŌĆō1h ŌĆō1 = (ŽĆ Ōüä 3p)2 Ōüä3, where kB is the Boltzmann constant, m* is the effective carrier mass, e is the electronic charge, h is the Planck constant, and p is the carrier concentration. Thus, from the relation between the Seebeck coefficient and the carrier concentration, the Seebeck coefficient decreased as the carrier concentration decreased with increasing Pr filling and Co substitution. As the temperature increased, the Seebeck coefficient showed a peak value because the carrier concentration increased dramatically owing to the intrinsic transition above a specific temperature. Therefore, the maximum value was observed between 723 and 823 K. The temperature for the intrinsic transition shifted to lower temperatures with increasing charge compensation of Co. The (La0.25Pr0.75)0.8Fe3CoSb12 showed the highest Seebeck coefficient of 168.2 ╬╝V K-1 at 723 K, which was higher than the value of 158.7 ╬╝V K-1 at 723 K for the fully-filled La0.75Pr0.25Fe3CoSb12 [21]. This was attributed to a lower carrier concentration caused by partial filling.
Figure 5 shows the temperature dependence of the power factor (PF) for (La1ŌłÆzPrz)0.8Fe4ŌłÆxCoxSb12. The PF increased with increasing temperature, and a maximum PF was found between 723 and 823 K owing to the trade-off relationship between the Seebeck coefficient and the electrical conductivity. However, the PF did not change significantly with the La/Pr filling ratio. The PF ranged from 1.45 to 2.62 mW m-1 K-2 at 323 K, and the (La0.75Pr0.25)0.8Fe3CoSb12 showed the highest PF of 2.67 mW m-1 K-2 at 823 K. The fully-filled specimens showed PF values ranging from 1.19 to 1.61 mW m-1 K-2 at 323 K, which were lower than those of the partially-filled specimens. However, the fully-filled La0.75Pr0.25Fe3CoSb12 showed the highest PF of 3.17 mW m-1 K-2 at 823 K [21], which was higher than those of the partially-filled specimens. Unlike the fully-filled specimens, the maximum PF was obtained for the x = 0.5 substitution, which was attributed to the optimal carrier concentration.
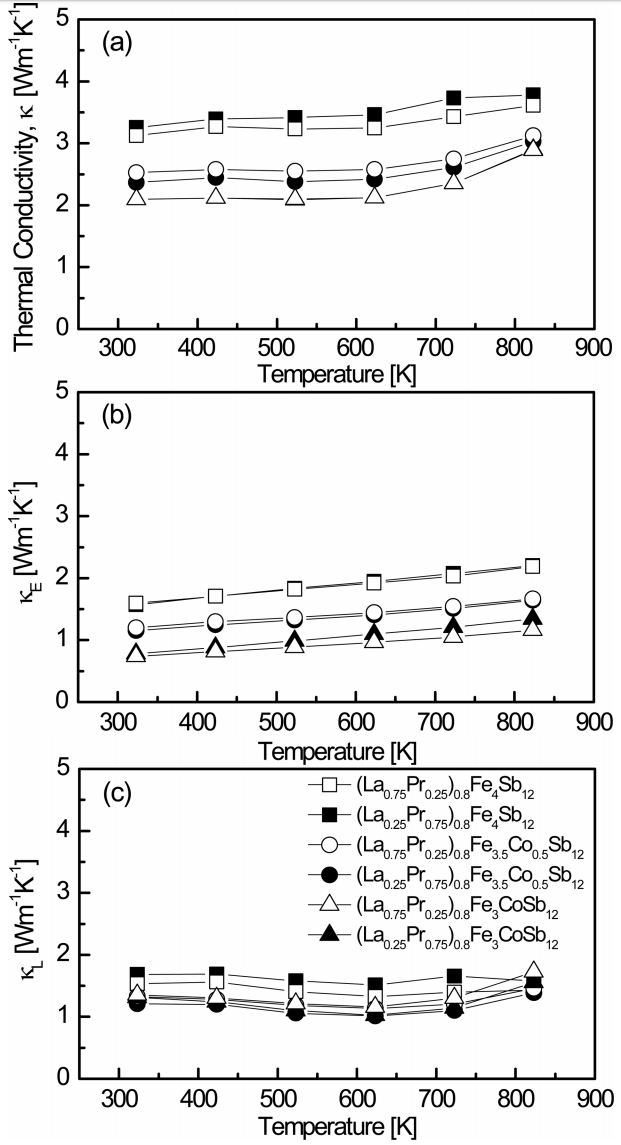
Figure 6 shows the temperature dependence of the thermal conductivity for (La1ŌłÆzPrz)0.8Fe4ŌłÆxCoxSb12. The thermal conductivity (╬║) is the sum of the lattice thermal conductivity (╬║L) and the electronic thermal conductivity (╬║E), which can be separated using the Wiedemann-Franz law (╬║E = LŽāT), where L is the Lorenz number, taken as 2.0 ├Ś 10ŌłÆ8 V2 KŌłÆ2 in this study [24]. As shown in Fig. 6(a), the change in thermal conductivity was more dominantly attributed to the Co content than the La/Pr filling ratio. The thermal conductivity decreased with increasing Co substitution, and the values of ╬║ = 2.09 ŌłÆ 3.78 W m-1 K-1 were observed in the measured temperature range. The thermal conductivity increased at temperatures above 623 K owing to the bipolar effect. The fully-filled La1ŌłÆzPrzFe1ŌłÆxCoxSb12 showed values of ╬║ = 2.18 ŌłÆ 3.10 W m-1 K-1 at temperatures between 323 and 823 K [21]. The (La0.25Pr0.75)0.8Fe3CoSb12 showed the lowest ╬║ of 2.09 W m-1 K-1 at 323 K, while the fully-filled La0.25Pr0.75Fe3CoSb12 showed the lowest ╬║ of 2.18 W m-1 K-1 at 323 K, which was slightly higher than the ╬║ of partially-filled (La0.25Pr0.75)0.8Fe3CoSb12. As shown in Fig. 6(b), the electronic thermal conductivity decreased with increasing Co substitution owing to the decreased carrier concentration caused by charge compensation. The (La0.75Pr0.25)0.8Fe3CoSb12 sample showed the lowest ╬║E of 0.74W m-1 K-1 at 323 K. The fully-filled La1ŌłÆzPrzFe1ŌłÆxCoxSb12 specimens showed higher values of ╬║E = 1.01 ŌłÆ 2.55 W m-1 K-1 [21] than the partially-filled specimens at all temperatures. As shown in Fig. 6(c), the values of ╬║L = 1.01 ŌłÆ1.51 W m-1 K-1 were obtained at 623 K, which were the lowest lattice thermal conductivities of all the specimens. The lattice thermal conductivity decreased with increasing phonon scattering owing to impurity (alloy) scattering in the Cosubstituted specimens, but the change in the lattice thermal conductivity caused by the filling ratio of La/Pr was small. The (La0.25Pr0.75)0.8Fe3.5Co0.5Sb12 showed the lowest ╬║L of 1.01 W m-1 K-1 at 623 K. The fully-filled La1ŌłÆzPrzFe4ŌłÆxCoxSb12 specimens showed the lowest ╬║L at temperatures between 623 and 723 K, and La0.25Pr0.75Fe4Sb12 showed the lowest ╬║L of 0.33 W m-1 K-1 at 723 K [21]. Compared to the fully-filled specimens, relatively higher ╬║L values were obtained for the partially-filled specimens. Filled skutterudites have been reported to be effective at improving phonon scattering as a result of low resonance frequency scattering due to heavy filler elements or small ionic radii of filler elements [15-22]. It was expected that the lattice thermal conductivity would be reduced by improving the phonon scattering using La and Pr as the filler elements, which are heavy and have small ionic radii. As mentioned above, the enhancement of the phonon scattering due to the similar atomic and ionic radii of La and Pr was insignificant compared with the complete double filling.
Figure 7 shows the temperature dependence of the dimensionless figure of merit (ZT) for (La1ŌłÆzPrz)0.8Fe4ŌłÆxCoxSb12. ZT increased with temperature, and maximum ZT values were obtained at temperatures between 723 and 823 K for the Co-substituted specimens. The (La0.25Pr0.75)0.8Fe3.5Co0.5Sb12 showed the maximum ZT = 0.79 at 723 K. However, the fully-filled La0.75Pr0.25Fe4Sb12 showed the maximum ZT = 0.83 at 823 K. In this study, La and Pr were used as filling elements for partial-double filling, and the carrier concentration optimization and the phonon scattering were expected to be enhanced by Co charge compensation. In addition, the improvement in phonon scattering was intended to improve thermoelectric performance by reducing the lattice thermal conductivity. However, the atomic mass and ionic radius were 138.9 and 0.136 nm for La and 140.9 and 0.133 nm for Pr, respectively; therefore, the differences in the atomic masses and ionic radii of La and Pr were not sufficient to cause a significant change in the lattice thermal conductivity as the La-to-Pr filling ratio was varied. At the same time, the improvement in phonon scattering by partialdouble filling was found to be insignificant, due to the very similar ionic radii and atomic masses of La and Pr. Therefore, the thermoelectric performance was not improved, compared to La1-zPrzFe4-xCoxSb12. In addition, Shin et al. [25] reported a ZTmax = 0.85 at 723 K for (Pr0.75Yb0.25)0.8Fe3CoSb12, Zhou et al. [26] reported a ZTmax = 0.99 at 700 K for Yb0.25La0.60Fe2.7Co1.3Sb12, and Rogl et al. [27] reported a ZTmax = 1.3 at 825 K for DD0.6Fe3CoSb12, where DD is didymium. In this study, when the Co was charge-compensated, the temperature range of the ZTmax shifted to lower temperatures, and thus applications for thermoelectric generation in the intermediate temperature range, were expected.
4. CONCLUSIONS
Partially double-filled p-type (La1ŌłÆzPrz)yFe4ŌłÆxCoxSb12 (z = 0.25, 0.75; y = 0.8; x = 0, 0.5, 1.0) skutterudites were synthesized by encapsulated melting and sintered by hot pressing. All specimens were transformed into the skutterudite phase by annealing, but the marcasite phase was also formed. However, (La,Pr)Sb2 phases were not produced and the amount of FeSb2 was significantly reduced by La/Pr partial filling and Co substitution. The Hall coefficient and the Seebeck coefficient values were positive, indicating that all specimens had p-type conduction characteristics. The Seebeck coefficient increased with increased Pr and Co contents, while the electrical conductivity decreased due to the decreased carrier concentration. Compared with the fullyfilled specimens, the partially-filled specimens showed slightly lower Seebeck coefficients and higher electrical conductivities due to the increased carrier concentration caused by partially filling. The partial double filling of La and Pr led to a higher lattice thermal conductivity. The maximum ZT value of 0.79 was obtained at 723 K for the (La0.25Pr0.75)0.8Fe3.5Co0.5Sb12.