1. INTRODUCTION
Skutterudite has a body-centered cubic structure (space group: Im3) with a framework of 8MX3 (M: Fe, Ru, Os, Co, Rh, Ir, Ni, Pd, and Pt, and X: P, As, and Sb) and two voids per unit cell. If the voids are filled with specific atoms (fillers or rattlers), the rattling effect of the fillers can greatly reduce the lattice thermal conductivity and thus improve the thermoelectric performance [1,2]. This skutterudite is called a filled skutterudite and, in general, the chemical formula RM4X12 (R: alkali, alkaline-earth, and rare-earth elements) is used. RCo4Sb12-based materials have been actively investigated for n-type filled skutterudites [3-5] and RFe4Sb12-based materials have been examined for p-type filled skutterudites [6-8]. RCo4Sb12 has 72 valence electron counts (VEC) but RFe4Sb12 has only 68 VEC, and thus needs additional electrons for charge compensation [9]. Therefore, to optimize the carrier concentration, substitutions such as Co or Ni for the Fe sites are required, in addition to filling the voids with R atoms.
Void filling is a very effective method for improving the thermoelectric performance of p-type skutterudites. The lattice thermal conductivity is reduced, by the fillers, which act as phonon scattering centers of a specific resonance frequency [4,6,10,11]. Using rare-earth elements with heavier atomic masses as fillers can reduce the lattice thermal conductivities by phonon scatterings of lower frequencies, and using two or more filler elements can broaden the range of scattering frequencies [4,5,7]. Therefore, when double or multiple filling with two or more fillers is performed, it is expected that the lattice thermal conductivity can be further reduced due to the enhanced phonon scattering and in this way the thermoelectric performance can be improved [5,11-13]. It has recently been reported that Co- and Ni-substituted p-type filled skutterudites are not completely filled [14-16]. In our previous study, Ce/Nd-double-filled and Co-substituted skutterudites with y = 1 produced (Ce,Nd)Sb2 phases because the Ce/Nd double filling exceeded the filling fraction limit [17]. In the present study, partially Ce/Nd-double-filled and Co-substituted (Ce1-zNdz)yFe4-xCoxSb12 skutterudites were prepared and their phase, microstructure, charge transport, and thermoelectric properties were examined.
2. EXPERIMENTAL PROCEDURE
(Ce1-zNdz)yFe1-xCoxSb12 (z = 0.25 or 0.75, y = 0.8, and x = 0, 0.5 or 1) skutterudites were synthesized by encapsulated melting. Elemental Ce (purity 99.9%, Sigma Aldrich), Nd (purity 99.9%, Kojundo), Fe (purity 99.95%, Cerac), Co (purity 99.95%, Alfa Aesar), and Sb (purity 99.999%, LTS) were melted at 1323 K for 10 h in an evacuated quartz tube coated on the inside with carbon and they were then quenched in water. The quenched ingot was annealed at 873 K for 24 h to homogenize the skutterudite phase. The annealed ingot was ground to a fine powder with a particle size of less than 75 ╬╝m, and then, the powder was hot pressed in a graphite die with an internal diameter of 10 mm at 898 K under 70MPa for 1 h in a vacuum.
An X-ray diffractometer (XRD, Bruker, D8-Advance) was used for phase analysis of the hot-pressed specimens. Cu-K╬▒ (40 kV and 30 mA) radiation was used and the diffraction patterns were measured in the ╬Ė-2╬Ė mode (2╬Ė = 10┬░ŌłÆ90┬░) with a scan speed of 0.4 sec/step, step size 0.02┬░, and wavelength 0.15405 nm. The microstructure was observed using a scanning electron microscope (SEM, FEI, Quanta400) and the chemical composition was analyzed by energy-dispersive spectroscopy (EDS, Bruker, Quantax200). The hot-pressed specimens were cut into rectangular pieces of 3 ├Ś 3 ├Ś 9 mm3 to measure both the Seebeck coefficient (╬▒) and electrical conductivity (Žā), and then they were cut into discs with dimensions of 10 mm (diameter) ├Ś 1 mm (thickness) to determine their thermal conductivity (╬║). Charge transport properties such as the Hall coefficient (RH), and carrier concentration (p) and mobility (m) were measured using a Keithley 7065 system at room temperature, with a constant magnetic field (1 T) and current (50 mA). The Seebeck coefficient and the electrical conductivity were measured with the ZEM-3 (Ulvac-Riko) equipment in a He atmosphere, and the thermal conductivity (╬║ = Dcpd) was evaluated by measuring the thermal diffusivity (D), specific heat (cp), and density (d) using the laser flash method with the TC-9000H (Ulvac-Riko) instrument, under vacuum. The electrical and thermal conductivities, the power factor (PF = ╬▒2Žā) and the dimensionless figure of merit (ZT = ╬▒2Žā╬ż╬║-1) were studied using the measured Seebeck coefficient.
3. RESULTS AND DISCUSSION
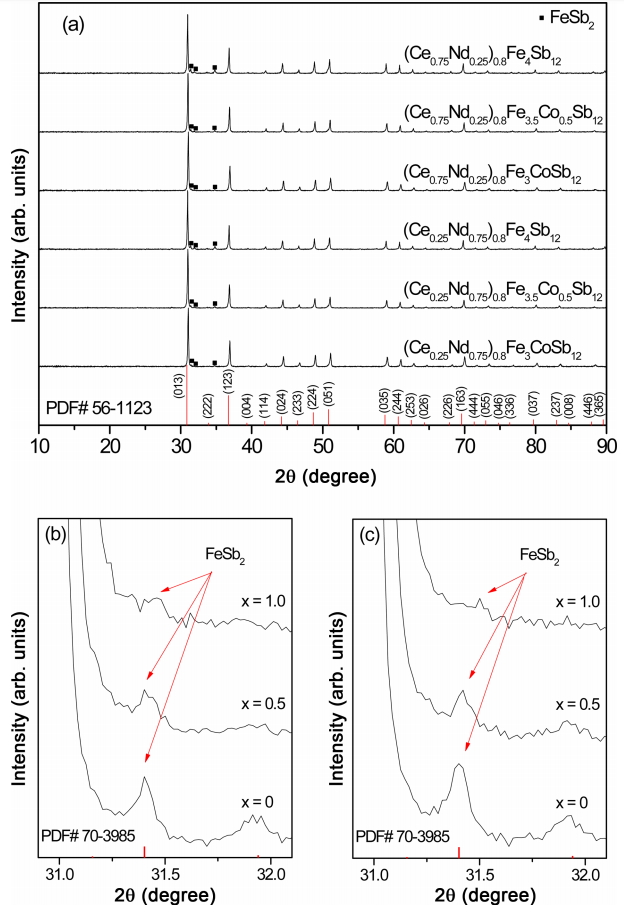
Figure 1 shows the XRD patterns of the (Ce1-zNdz)0.8Fe4-xCoxSb12 skutterudites. Diffraction peaks corresponded to the standard data for the skutterudite phase (ICDD PDF# 56-1123); a small amount of the marcasite (FeSb2) phase (ICDD PDF# 70-3985) was also identified. As shown in Fig. 1(b) and 1(c), peak intensity decreased with increasing Co content, and the formation of the marcasite phase was suppressed by the void filling and charge compensation. The diffraction peaks shifted to higher angles with increasing Co content, which indicated that the lattice constant decreased because the atomic radius of Co (0.167 nm) was smaller than that of Fe (0.172 nm).
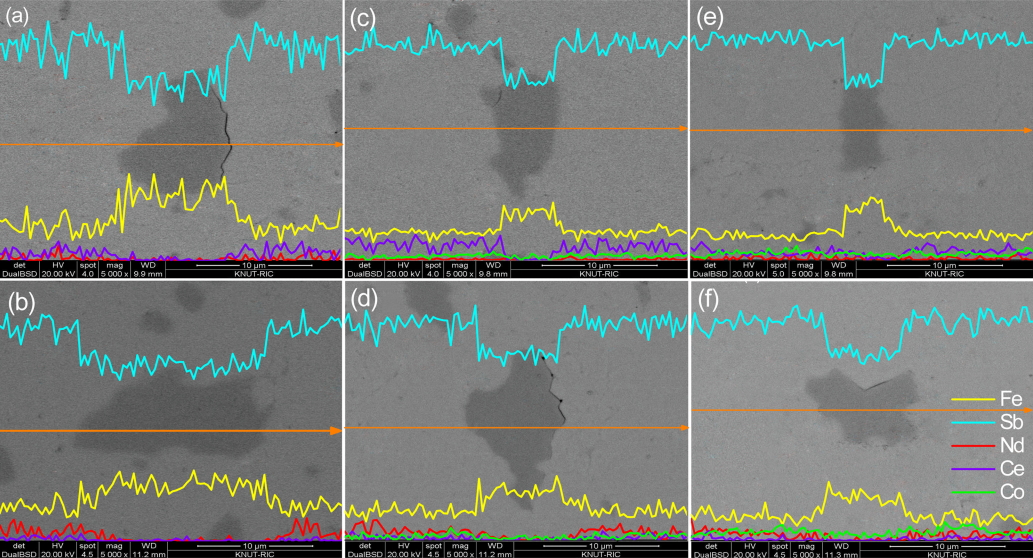
Figure 2 represents SEM images and EDS line scans of (Ce1-zNdz)0.8Fe4-xCoxSb12. The FeSb2 phase (dark region) was observed with the skutterudite phase (bright region) in all specimens; however, the formation of the FeSb2 phase was inhibited by the increasing Co content. This behavior was consistent with the XRD results. Song et al. [17] observed (Ce,Nd)Sb2 phases in the completely filled Ce1-zNdzFe3.5Co0.5Sb12; however, in the present study, (Ce,Nd)Sb2 phases were not produced in the partially filled (Ce1-zNdz)0.8Fe4-xCoxSb12 because the partial filling of the specimen did not exceed the filling fraction limit.
Table 1 shows the chemical composition and lattice constants of the (Ce1-zNdz)0.8Fe4-xCoxSb12. All specimens showed a density of over 98% of the theoretical density. Actual compositions showed slight differences from nominal compositions, possibly due to the oxidation of Ce and Nd and the volatilization of Sb during the synthesis and consolidation processes at high temperatures. The calculated lattice constants ranged from 0.9100 to 0.9127 nm, depending on the Ce/Nd filling ratio and Co substitution amount, and decreased with increasing Co content. However, there was almost no difference in the lattice constant with the variation in the Ce/Nd filling ratio, despite the difference in ionic radius between Ce (0.134 nm) and Nd (0.127 nm). In general, the lattice constant increases with increasing filling fraction, within the filling fraction limit. However, in the present study, all specimens with y = 0.8 reached the filling fraction limit; thus, the total filling fraction for each specimen was identical and, therefore, the change in the lattice constant with the variation of the Ce/Nd filling ratio was negligible.
The charge transport properties of (Ce1-zNdz)0.8Fe4-xCoxSb12 at room temperature are shown in Table 1. All specimens exhibited positive signs of Hall coefficient, confirming that the majority carrier is a hole of a p-type semiconductor. As the amount of Co substitution increased, the carrier concentration decreased, because electrons were supplied by the charge compensation of Co to Fe. The carrier concentration changed slightly with the Ce/Nd filling ratio. The partially filled specimens (y = 0.8 and x = 0ŌĆō0.5) showed higher carrier concentrations, ranging from 1.58 ├Ś 1021 to 4.56 ├Ś 1021 cm-3, while the completely filled specimens (y = 1 and x = 0 ŌĆō 0.5) had values in the range of 1.29 ├Ś 1021 to 2.82 ├Ś 1021 cm-3 [17]. This difference results from the increase in carrier concentration due to electron shortage.
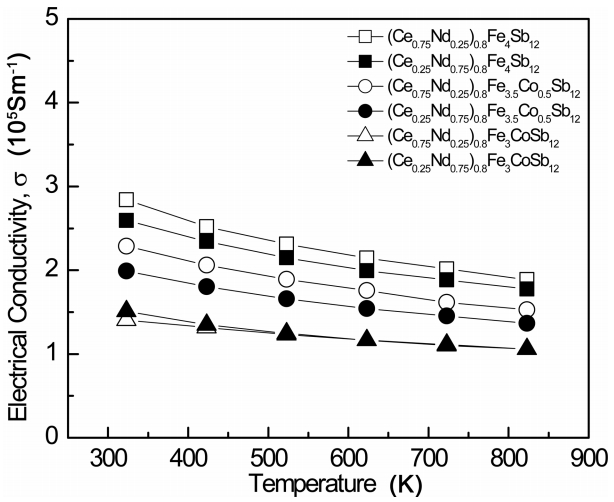
Figure 3 presents the temperature dependence of the electrical conductivity of (Ce1-zNdz)0.8Fe4-xCoxSb12. The electrical conductivities slightly decreased with increasing temperature, indicating that the specimens were degenerate semiconductors. The electrical conductivity decreased with increasing Co content due to the increased carrier concentration. In addition, higher electrical conductivity was obtained in specimens where the filling fraction of Ce was higher than that of Nd. This was consistent with the carrier concentration change shown in Table 1. The electrical conductivities of the partially filled specimens ranged from 1.51 ├Ś 105 to 2.84 ├Ś 105 Sm-1 at 323 K, and were higher than those (1.53 ├Ś 105 to 2.05 ├Ś 105 Sm-1 at 323 K) of the completely filled specimens [17].
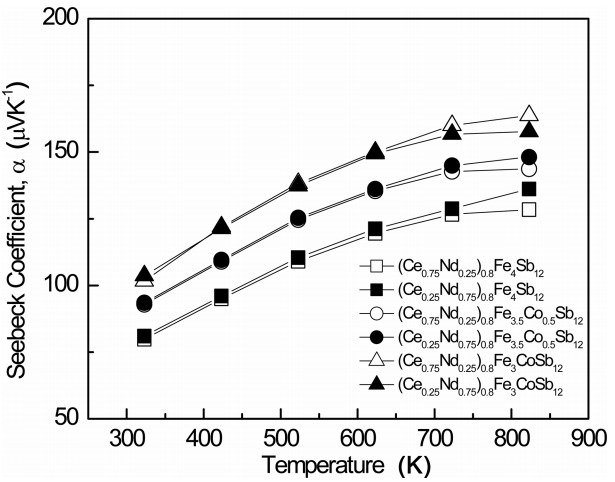
Figure 4 shows the temperature dependence of the Seebeck coefficient of (Ce1-zNdz)0.8Fe4-xCoxSb12. Like the Hall coefficient values listed in Table 1, the positive sign of the Seebeck coefficient implies p-type conduction. The Seebeck coefficient increased with temperature and the Co-substituted specimens showed a maximum at 823 K due to intrinsic conduction. In addition, the Seebeck coefficient increased with increasing Co content. The Seebeck coefficient is inversely proportional to the carrier concentration and is expressed as ╬▒ = (8Ōüä3)ŽĆ2k2Bm*TeŌĆō1hŌĆō1(ŽĆŌüä3n)2Ōüä3, where kB is the Boltzmann constant, m* is the effective carrier mass, T is the absolute temperature, e is the electronic charge, h is the Planck constant, and n is the carrier concentration. Therefore, as the Nd filling and the Co substitution increased, the carrier (hole) concentration decreased and the Seebeck coefficient increased. (Ce0.75Nd0.25)0.8Fe3CoSb12 showed a maximum Seebeck coefficient of 157.7 ╬╝VK-1 at 823 K while Ce0.25Nd0.75Fe3.5Co0.5Sb12 showed 160.2 ╬╝VK-1 at 723 K [17]. A comparison of the maximum Seebeck coefficients showed that the partially filled specimens exhibited lower values than the completely filled ones. This was because the carrier concentrations of the partially filled specimens were higher than those of the completely filled ones.
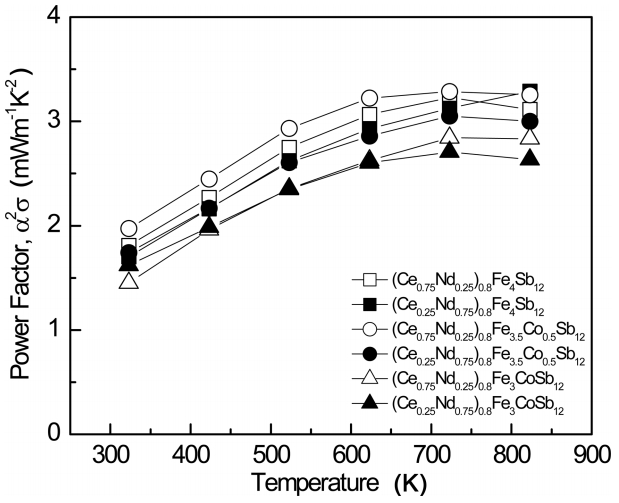
Figure 5 presents the variation of the power factor (PF) for (Ce1-zNdz)0.8Fe4-xCoxSb12. The Seebeck coefficient and the electrical conductivity have a tradeoff relation which can be expressed as PF = ╬▒2Žā. Because both depend on the carrier concentration, the specimen with an optimum carrier concentration exhibits a maximum PF value. The maximum PF values were obtained for the Co-substituted (x = 0.5) specimens with higher Ce filling and for non-substituted (x = 0) specimens with higher Nd filling. Partial filling resulted in improved PF values due to the increased electrical conductivity, thus (Ce1-zNdz)0.8Fe4-xCoxSb12 showed PF values of 2.63 to 3.29 mWm-1K-2 at 823 K while Ce1-zNdzFe4-xCoxSb12 showed PF values of 2.32 to 3.14 mWm-1K-2 at 823 K [17].
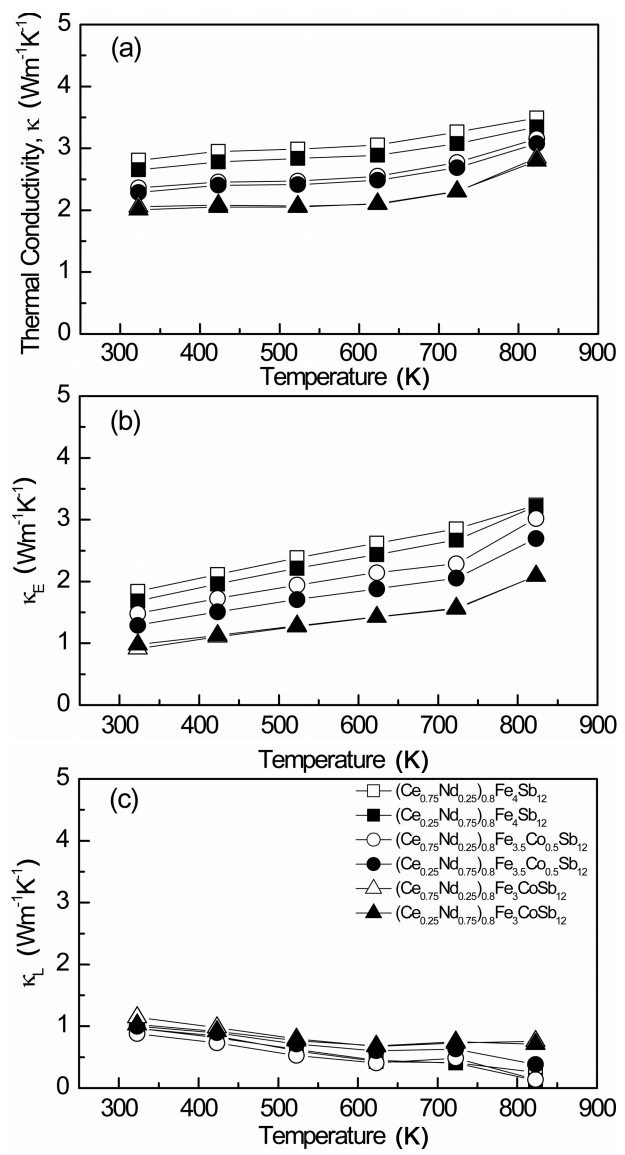
Figure 6 shows the temperature dependence of the thermal conductivity of (Ce1-zNdz)0.8Fe4-xCoxSb12. As shown in Fig. 6(a), the partially filled specimens showed thermal conductivities ranging from 2.00 to 2.81 Wm-1K-1 at 323 K, which slightly increased above 723 K due to bipolar conduction. The thermal conductivity (╬║) is expressed as the sum of the lattice thermal conductivity (╬║L) and the electronic thermal conductivity (╬║E). The ╬║E value can be calculated from the Wiedemann-Franz law (╬║E = LŽāT), where L is the Lorenz number, taken, for this study, as 2.0 ├Ś 10ŌłÆ8V2 KŌłÆ2. The calculated ╬║E values are presented in Fig. 6 (b). (Ce1-zNdz)0.8Fe4Sb12 showed higher ╬║E values (1.68 to 3.23 Wm-1K-1) than those of Ce1-zNdzFe4Sb12 (1.00 to 2.22 Wm-1K-1) [17]. This behavior results from the higher carrier concentration of (Ce1-zNdz)0.8Fe4Sb12 and the presence of the marcasite, which has higher electrical and thermal conductivities than the skutterudite [17]. However, (Ce1-zNdz)0.8Fe3CoSb12 exhibited relatively low ╬║E values of 0.91 Wm-1K-1 to 2.09 Wm-1K-1 due to low carrier concentration and stable skutterudite phases. The separated ╬║L values are shown in Fig. 6(c). (Ce1-zNdz)0.8FexCo1-xSb12 exhibited very low ╬║L values of 0.12 to 1.14 Wm-1K-1 at all temperatures. To reduce the lattice thermal conductivity of the p-type single-filled skutterudites, low-resonance frequency scattering by fillers with heavy atomic masses and small ionic radii, which enhance phonon scattering, is effective [11,18]. The lattice thermal conductivity was expected to be lowered by double filling of Ce and Nd, but its further reduction was not significant, due to the similar atomic mass and ionic radius of Ce (140.1 and 0.134 nm) and Nd (144.2 and 0.127 nm).
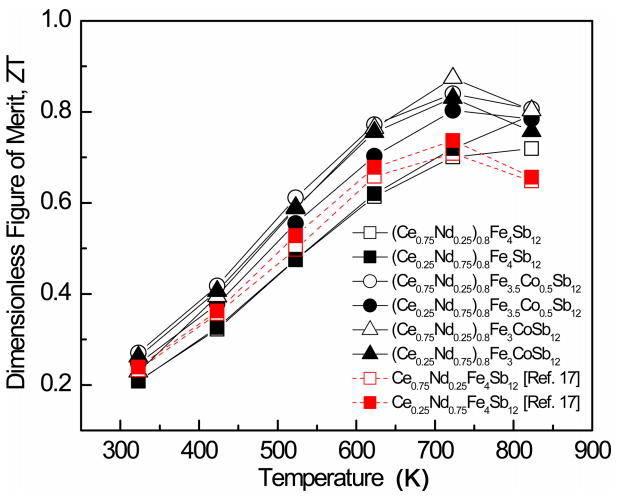
Figure 7 presents the temperature dependence of the dimensionless figure-of-merit (ZT) for (Ce1-zNdz)0.8Fe4-xCoxSb12. ZT increased with temperature and reached a maximum at temperatures above 723 K due to the onset of intrinsic transition and bipolar conduction. The thermoelectric performance was expected to improve due to the optimized carrier concentration and the enhanced phonon scattering obtained by the charge compensation of Co and the partial double-filling of Ce/Nd. The ZT values of the partially filled specimens exhibited significant improvements as compared with those of the completely filled Ce1-zNdzFe4-xCoxSb12 specimens. (Ce0.75Nd0.25)0.8Fe3CoSb12 had a ZTmax of 0.87 at 723 K while that for Ce0.25Nd0.75Fe4Sb12 was 0.73 at 723 K [17]. Joo et al. [19] reported a ZTmax of 0.77 at 723K for Ce0.75Yb0.25Fe3CoSb12, and Shin et al. [20] reported a ZTmax of 0.84 at 723 K for (Pr0.75Nd0.25)0.8Fe3CoSb12. A higher ZT for (Ce0.75Nd0.25)0.8Fe3CoSb12, at the same temperature, was obtained in the present study. ZT values were improved in the specimens by partial filling and carrier concentration compensation control; however, they were lower than those in other double- or multiple-filled skutterudites [21-24]. Partial double-filling with filler elements having large differences in atomic mass and ionic radius is expected to improve thermoelectric properties.
4. CONCLUSION
Partially double-filled p-type (Ce1-zNdz)yFe4-xCoxSb12 (z = 0.25 or 0.75; y = 0.8; x = 0, 0.5 or 1.0) skutterudites were prepared by encapsulated melting, annealing, and hot pressing. All specimens were transformed into the skutterudite phase by heat treatment but a small amount of marcasite phase was also detected. However, void filling with Ce/Nd and Co substitution can inhibit the formation of the marcasite phase. The partially filled specimens did not exceed the filling fraction limit, which was taken to be y = 0.8. Thus, (Ce,Nd)Sb2 phases were not formed in this study. Both the Seebeck and Hall coefficient values were positive, indicating that all specimens exhibited p-type characteristics. The Seebeck coefficient increased with increasing Co and Nd contents, while the electrical conductivity decreased. In addition, partial filling slightly increased the electrical conductivity but decreased the Seebeck coefficient. The partial double-filling of Ce and Nd could not further reduce the thermal conductivity, compared with the complete double-filling. A maximum dimensionless figure of merit, ZTmax= 0.87, was obtained at 723 K for (Ce0.75Nd0.25)0.8Fe3CoSb12.