Thermoelectric Performance of Sn and Bi Double-Doped Permingeatite

Article information

Abstract

1. INTRODUCTION

Thermoelectric power generation has attracted significant interest as an eco-friendly and energy-efficient technique because it directly converts waste heat energy into electrical energy [1]. Recently, permingeatite (Cu₃SbSe₄) has been investigated for thermoelectric applications [2]. Cu₃SbSe₄ exhibits a tetragonal (space group I4¯2m) structure, where Cu is ionized into Cu⁺ and Cu²⁺ to form distorted CuSe₄ tetrahedra and flat SbSe₄ tetrahedra, which enhance phonon scattering [3]. Permingeatite is of particular interest because it can result in low thermal conductivity through anharmonic vibrations [4]. In addition, its large effective mass (1.1 m_o) and narrow band gap (0.29-0.40 eV) are advantageous for thermoelectric applications [5].

Thermoelectric performance is evaluated based on a power factor (PF = α²σ) and dimensionless figure-of-merit (ZT = α²σκ-1T), which is affected by the Seebeck coefficient (α), electrical conductivity (σ), and thermal conductivity (κ) of a material at the application temperature (T, in units of Kelvin). To improve the thermoelectric performance of permingeatite, a number of studies have focused on substitution (doping) at the Cu site. For example, Kumar et al. [6,7] reported ZT values of 0.35 at 475 K for Cu_2.5Zn_0.5SbSe₄ and 0.65 at 650 K for Cu_2.99Ni_0.01SbSe₄. Doping of various elements at Sb sites has been extensively reported on efforts to reduce thermal conductivity by phonon scattering. Zhao et al. [8] reported a ZT of 0.54 at 605 K for Cu₃Sb_0.985Ga_0.015Se₄; Chang et al. [9] obtained a ZT of 0.54 at 640 K for Cu_2.95Sb_0.96Ge_0.04Se₄; Zhang et al. [10] achieved a ZT of 0.50 at 648 K for Cu₃Sb_0.997In_0.003Se₄; Li et al. [11] reported a ZT of 0.58 at 600 K for Cu₃Sb_0.97Al_0.03Se₄. In addition, Kumar et al. [12] investigated double doping at Sb and Se sites and reported a ZT of 0.76 at 650 K for Cu₃Sb_0.98Bi_0.02Se_3.99Te_0.01. Liu et al. [13] obtained a high ZT of 1.26 at 673 K for Cu₃Sb_0.88Sn_0.1Bi_0.02Se₄, where Sn and Bi were double doped at the Sb site using a multistep solution-based synthesis.

In our previous study [14], famatinite (Cu₃SbS₄; space group I4¯2m) with a crystal structure similar to that of permingeatite was successfully and easily synthesized via mechanical alloying (MA) as a one-step solid-state method without subsequent heat treatment. In this study, Cu₃Sb_1-x-ySn_xBi_ySe₄ with partial double doping at the Sb site was prepared via MA and hot pressing (HP), and the effects of double doping Sn and Bi on thermoelectric performance were investigated.

2. EXPERIMENTAL PROCEDURE

Sn/Bi double-doped permingeatites Cu₃Sb_1-x-ySn_xBi_ySe₄ (x = 0.02, 0.04, and 0.06; y = 0.02 and 0.04) were synthesized via MA. The compositions of the specimens were designed to be x + y = 0.06 or 0.08. Cu (< 45 μm, purity 99.9%), Sb (< 150 μm, purity 99.999%), Sn (< 35 μm, purity 99.999%), Bi (< 180 μm, purity 99.999%), and Se (< 10 μm, purity 99.9%) powders were used as the starting materials for MA. A planetary ball milling system (Pulverisette5, Fritsch) was employed with hardened steel jars and balls, and MA was conducted at 350 rpm for 12 h in an Ar atmosphere. Then, the synthesized powder was consolidated using HP at 573 K for 2 h under 70 MPa in vacuum.

X-ray diffraction (XRD; D8-Advance, Bruker) was performed using Cu–Kα radiation to analyze the phases of the specimens. The lattice constants were estimated using Rietveld refinement (TOPAS, Bruker). Scanning electron microscopy (SEM; Quanta400, FEI) was performed to observe the microstructures of the HP specimens. The chemical composition was analyzed using energy-dispersive spectroscopy (EDS; Quantax200, Oxford Instruments). The van der Pauw (7065, Keithley) method was used and a single-valley model was assumed to measure the charge transport parameters under the conditions of 1 T and 100 mA_DC. A four-probe system (ZEM-3, Advance Riko) was used to measure the Seebeck coefficient and electrical conductivity. Laser flash equipment (TC-9000H, Advance Riko) was used to measure the thermal diffusivity, and the thermal conductivity was calculated using the density and specific heat of the specimens. Finally, the PF and ZT values were evaluated.

3. RESULTS AND DISCUSSION

Fig 1 shows the results of the phase analysis of Cu₃Sb_1-x-ySn_xBi_ySe₄ synthesized via MA–HP. Phase changes caused by Sn and Bi contents were not observed, and a single-phase tetragonal permingeatite (ICDD PDF#085–0003) was achieved. The lattice constant of Cu₃Sb_1-x-ySn_xBi_ySe₄, as shown in Table 1, decreased from 0.56518 to 0.56515 nm for the a-axis and from 1.12525 to 1.12515 nm for the c-axis as the Bi content increased. However, as the Sn content increased, that of the a-axis decreased to 0.56510 nm, but that of the c-axis increased to 1.12529 nm. Because the lattice constants of undoped Cu₃SbSe₄ are a = 0.564 nm and c = 1.128 nm [13, 15], when Sn and Bi were double doped in this study, the a-axis increased, and the c-axis decreased. Prasad et al. [16] reported that as the Sn content of Cu₃Sb_1-xSn_xSe₄ (x = 0.00-0.04) increased, the degree of disorder at the cation site increased, and the lattice volume decreased because of a decrease in the anti-site defect SnSb or an increase in SbSn. In contrast, Yang et al. [17] reported that the lattice of Cu₃Sb_1-xSn_xSe₄ (x = 0-0.05) expanded with Sn content, owing to the larger ionic radius of Sn⁴⁺ compared with that of Sb⁵⁺. Li et al. [18] suggested the occurrence of lattice distortion and point defects (V_Cu or V_Sb); hence, the lattice constant increased when Bi was doped at the Sb site because the radius of Bi⁵⁺ was larger than that of Sb⁵⁺. Liu et al. [13] discovered that lattice expansion occurred because of the simultaneous replacement of the larger cations Sn⁴⁺ (69 pm) and Bi⁵⁺ (76 pm) compared with that of Sb⁵⁺ (60 pm).

Fig. 1.

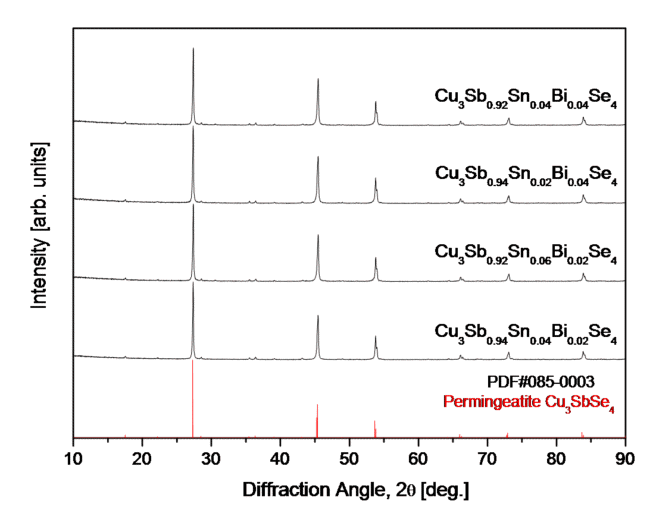
XRD patterns of Cu₃Sb_1-x-ySn_xBi_ySe₄ permingeatite synthesized via mechanical alloying and hot pressing.

Table 1.

Chemical compositions and physical properties of Cu₃Sb_1-x-ySn_xBi_ySe₄.

Fig 2 presents the fractured surfaces of sintered Cu₃Sb_1-x-ySn_xBi_ySe₄. It was observed that the Sn and Bi contents did not affect the microstructure. In addition, no unreacted residual elements or secondary phases were observed. The right column in the SEM images shows the EDS elemental maps of Cu₃Sb_0.92Sn_0.06Bi_0.02Se₄, which indicate that each element was homogeneously distributed. The relative density of the Sn/Bi double-doped permingeatite was 97.7%–98.2% (Table 1); the actual and nominal compositions did not differ significantly, and they were within the measurement error range. Therefore, a single permingeatite phase double-doped with Sn and Bi was successfully synthesized via MA and HP.

Fig. 2.

SEM images of fractured surfaces for Cu₃Sb_1-x-ySn_xBi_ySe₄ and EDS elemental maps of Cu₃Sb_0.92Sn_0.06Bi_0.02Se₄.

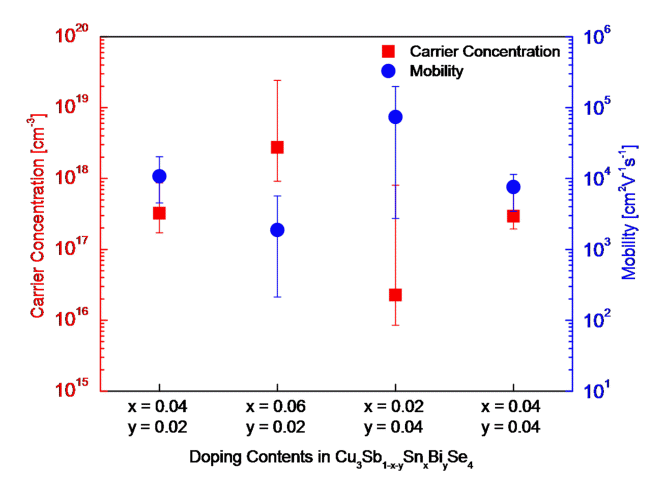
The charge transport characteristics of Cu₃Sb_1-x-ySn_xBi_ySe₄ are shown in Fig 3. The Hall coefficient values were positive, confirming that the majority charge carrier was holes in the p-type semiconductor. When the Bi content (y) was constant, the carrier concentration increased with the Sn content (x), i.e., from 3.24 × 10¹⁷ to 2.75 × 10¹⁸ cm^-3 when y = 0.02, and from 2.28 × 10¹⁶ to 2.93 × 10¹⁷ cm^-3 when y = 0.04. This was due to the additional holes generated by doping Sn⁴⁺ at the Sb⁵⁺ site. When the Sn content was constant, the change in the carrier concentration was insignificant, based on the Bi content. This was attributed to the valences of Bi⁵⁺ and Sb⁵⁺. Wei et al. [5] reported that Sn doping increased the carrier concentration of Cu_2.95Sb_1-xSn_xSe₄ (x = 0.00-0.04) from 5.02 × 1019 to 2.08 × 10²⁰cm^-3. Li et al. [18] achieved an increased carrier concentration in Cu₃Sb_1-yBi_ySe₄ (y = 0.00-0.03), i.e., from 3.38 × 10¹⁸ to 7.21 × 10¹⁸ cm^-3; however, it decreased to 2.89 × 10¹⁸ cm^-3 when y = 0.03 owing to the presence of impurity phases.

Fig. 3.

Charge transport properties of Cu₃Sb_1-x-ySn_xBi_ySe₄.

In this study, when the Bi content was constant, the mobility decreased significantly as the Sn content increased, i.e., from 1.07 × 10⁴ to 1.88 × 10³ cm²V^-1s^-1 when y = 0.02 and from 7.39 × 10⁴ to 7.59 × 10³ cm²V^-1s^-1 when y = 0.04. However, when the Sn content was constant, the mobility slightly decreased from 1.07 × 10⁴ to 7.59 × 10³ cm²V^-1s^-1 depending on the Bi content. Wei et al. [5] reported that as the Sn content increased in Cu₃Sb_1-xSn_xSe₄ (x = 0.01-0.04), the mobility decreased from 49 to 26 cm²V^-1s^-1. Li et al. [18] reported that as the Bi content increased in Cu₃Sb_1-yBi_ySe₄ (y = 0.01-0.03), the mobility decreased from 1.65 × 10² to 1.06 × 10² cm²V^-1s^-1.

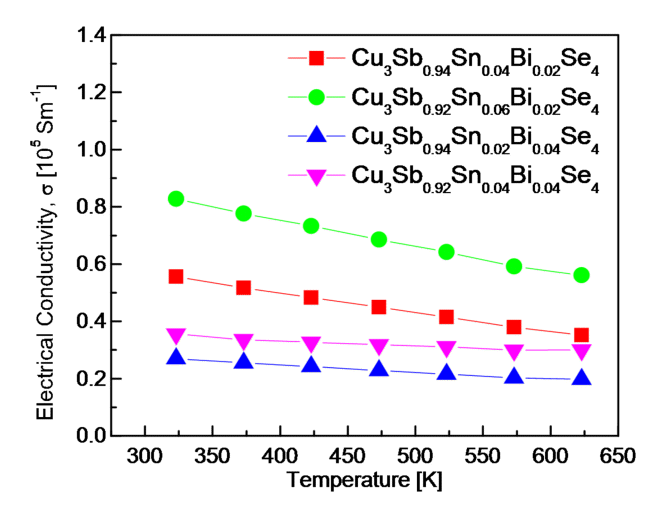
Fig 4 shows the electrical conductivity of Cu₃Sb_1-x-ySn_xBi_ySe₄. The electrical conductivity of a degenerate semiconductor is defined as σ = enμ (where e, n and μ are the electronic charge, the carrier concentration and the mobility, respectively) [19]. Therefore, electrical conductivity is affected by the temperature dependence of the carrier concentration and mobility. When the Bi content (y) was constant, the electrical conductivity increased with the Sn content (x), because of the increase in carrier concentration. In the temperature range of 323-623 K, the electrical conductivity increased from (5.56-3.51) × 10⁴ to (8.28-5.61) × 10⁴ Sm^-1 for x = 0.04-0.06 when y = 0.02, whereas it increased from (2.69-1.97) × 10⁴ to (3.56-3.00) × 10⁴ Sm^-1 for x = 0.02-0.04 when y = 0.04. However, when the Sn content was constant, the electrical conductivity decreased slightly as the Bi content increased, due to changes in the carrier concentration and mobility, as shown in Fig 3. Consequently, Cu₃Sb_0.92Sn_0.06Bi_0.02Se₄ exhibited the highest electrical conductivity, whereas Cu₃Sb_0.94Sn_0.02Bi_0.04Se₄ exhibited the lowest electrical conductivity.

Fig. 4.

Temperature dependence of electrical conductivity for Cu₃Sb_1-x-ySn_xBi_ySe₄.

Lee et al. [20] reported that the minimum electrical conductivity of Cu₃SbSe₄ was (4.23-4.88) × 10³ Sm^-1 at 323-623 K, which indicated nondegenerate semiconductor behavior. Compared with the undoped permingeatite, the electrical conductivity of permingeatite double-doped with Sn/Bi improved significantly in this study. Wei et al. [5] reported that electrical conductivity increased with Sn content in Cu₃Sb_1-xSn_xSe₄ (x = 0.01-0.04), where the highest electrical conductivity was 4.76 × 10³ Sm^-1 at 673 K for Cu₃Sb_0.96Sn_0.04Se₄. Li et al. [18] obtained the highest electrical conductivity of 1.11 × 10⁴ Sm^-1 at 600 K for Cu₃Sb_0.98Bi_0.02Se₄, among Cu₃Sb_1-yBi_ySe₄ (y = 0.01-0.03). Liu et al. [13] investigated double-doped Cu₃Sb_1-x-ySn_xBi_ySe₄ (x = 0.02-0.10 and y = 0.02) and obtained the highest electrical conductivity of 7.85 × 10⁴ Sm^-1 at 673 K for Cu₃Sb_0.88Sn_0.10Bi_0.02Se₄.

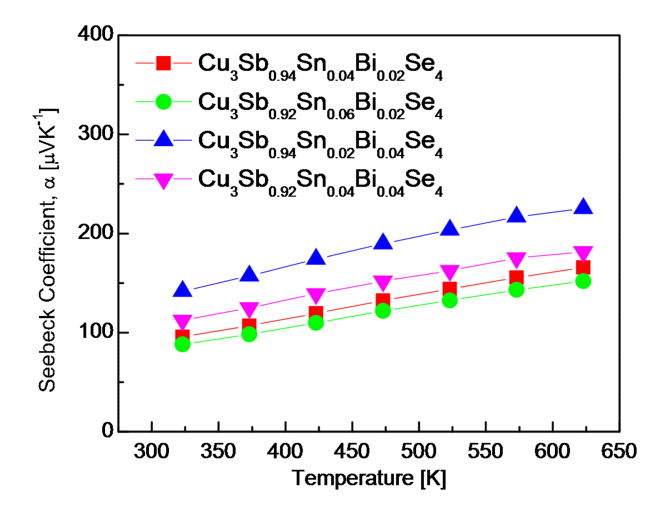
Fig 5 shows the Seebeck coefficients of Cu₃Sb_1-x-ySn_xBi_ySe₄. The permingeatite double-doped with Sn/Bi was a p-type semiconductor, which was reconfirmed from the positive Seebeck coefficient. The Seebeck coefficient is defined as a = (8/3)(π/3n)^2/3(πk_B/h)²m^*Te^-1 (where k_B, h and m^* are the Boltzmann constant, the Planck constant and the effective carrier mass, respectively) [21]. Because the Seebeck coefficient is inversely proportional to carrier concentration, it exhibits an opposite trend to the electrical conductivity. At a constant temperature, when the Bi content was constant, the Seebeck coefficient decreased with increasing Sn content, whereas when the Sn content was constant, the Seebeck coefficient increased with Bi content. Consequently, Cu₃Sb_0.94Sn_0.02Bi_0.04Se₄ exhibited a maximum Seebeck coefficient of 141-225 μVK^-1 at 323-623 K. Lee et al. [20] reported a Seebeck coefficient of 312-330 μVK^-1 at 323-623 K for undoped Cu₃SbSe₄. Wei et al. [5] obtained a lower Seebeck coefficient by doping Sn into Cu_2.95Sb_1-xSn_xSe₄ (x = 0.01-0.04); they obtained a maximum Seebeck coefficient of 163-249 μVK^-1 at 300-673 K for Cu₃Sb_0.99Sn_0.01Se₄. Li et al. [18] discovered that an intrinsic transition occurred at temperatures above 400 K for Cu₃Sb_1-xBi_xSe₄ (x = 0.01-0.03), which resulted in a maximum Seebeck coefficient of 417 μVK^-1 at 400 K for Cu₃Sb_0.98Bi_0.02Se₄. Liu et al. [13] reported that the double doping of Sn and Bi effectively increased the Seebeck coefficient of Cu₃Sb_1-x-ySn_xBi_ySe₄ (x = 0.02-0.10 and y = 0.02), and that Cu₃Sb_0.96Sn_0.02Bi_0.02Se₄ achieved a maximum Seebeck coefficient of 149-279 μVK^-1 at 323-673 K.

Fig. 5.

Temperature dependence of Seebeck coefficient for Cu₃Sb_1-x-ySn_xBi_ySe₄.

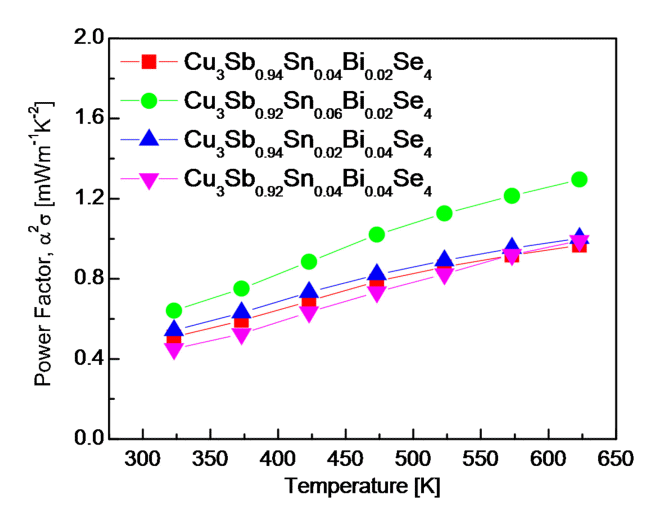
Fig 6 shows the PF of Cu₃Sb_1-x-ySn_xBi_ySe₄. The PF depends on the electrical conductivity and Seebeck coefficient, and these two parameters are affected oppositely by the carrier concentration [22]. The PF increased with temperature because the effect of increasing the Seebeck coefficient was greater than that of decreasing electrical conductivity caused by an increase in temperature. At a constant temperature, however, the increase in electrical conductivity by Sn/Bi double doping was more effective at increasing the PF than the decrease in the Seebeck coefficient. Consequently, Cu₃Sb_0.92Sn_0.06Bi_0.02Se₄ achieved the highest PF of 0.64-1.29 mWm^-1K^-2 at 323-623 K. Compared with the PF of undoped Cu₃SbSe₄ (0.38-0.50 mWm^-1K^-2 at 323-623 K) [20], Cu₃SbSe₄ double-doped with Sn/Bi significantly increased the PF of permingeatite. Wei et al. [5] obtained a PF of 0.65-1.38 mWm^-1K^-2 at 300-673 K for Cu₃Sb_0.97Sn_0.03Se₄. Li et al. [18] reported that the PF decreased with temperature from 1.8 mWm^-1K^-2 at 323 K to 1.1 mWm^-1K^-2 at 600 K for Cu₃Sb_0.98Bi_0.02Se₄. In fact, Liu et al. [13] further increased the Seebeck coefficient by performing Sn/Bi double doping (as compared with only Sn doping) and achieved the highest PF of 1.81 mWm^-1K^-2 at 654 K for Cu₃Sb_0.88Sn_0.1Bi_0.02Se₄.

Fig. 6.

Temperature dependence of power factor for Cu₃Sb_1-x-ySn_xBi_ySe₄.

The thermal conductivities of Cu₃Sb_1-x-ySn_xBi_ySe₄ are shown in Fig 7. After determining the electronic thermal conductivity (κ_E) using the Wiedemann–Franz law (κ_E = LσT), the lattice thermal conductivity (κ_L) was calculated from the measured thermal conductivity (κ) using the relation κ = κ_E+ κ_L [23,24], where the temperature-dependent Lorenz number (L) was estimated using the equation L = 1.5+ exp(– α ⁄ 116) [25, 26]. In this study, a specific heat of 0.32 Jg^-1K^-1 was used to evaluate the thermal conductivity [27], and Fig 7(a) shows the thermal conductivity of Cu₃Sb_1-x-ySn_xBi_ySe₄. The thermal conductivity decreased with temperature, and bipolar conduction did not occur within the measurement temperature range. At a constant temperature, the thermal conductivity decreased at higher Bi and lower Sn contents. However, a lower thermal conductivity was obtained at 523 K as the Bi content increased when the Sn content was constant at x = 0.04. Additionally, higher thermal conductivity was observed at temperatures above 523 K. This crossover in the thermal conductivity was similarly reported in Bi-doped permingeatite by Li et al. [18]. In this study, the lowest thermal conductivity of 1.40-0.91 Wm^-1K^-1 was obtained at 323-623 K in Cu₃Sb_0.94Sn_0.02Bi_0.04Se₄. Wei et al. [5] reported a minimum thermal conductivity of 3.19-1.21 Wm^-1K^-1 at 275-700 K for Cu_2.95Sb_0.99Sn_0.01Se₄. Li et al. [18] obtained a minimum thermal conductivity of 1.97-0.98 Wm^-1K^-1 at 323-573 K for Cu₃Sb_0.98Bi_0.02Se₄. Liu et al. [13] reported the lowest thermal conductivity of 1.20-0.94 Wm^-1K^-1 at 323-673 K in Cu₃Sb_0.96Sn_0.02Bi_0.02Se₄.

Fig. 7.

Temperature dependence of thermal conductivities of Cu₃Sb_1-x-ySn_xBi_ySe₄: (a) Total thermal conductivity and (b) electronic and lattice thermal conductivities.

Fig 7(b) shows the separate contributions to thermal conductivity. κ_E was attributed to the charge carriers, and κ_L was due to phonons. κ_E did not indicate a significant temperature dependence; however, it was directly affected by the carrier concentration, i.e., the Sn/Bi doping concentration. κ_E decreased because of the reduced carrier concentration as the Bi content increased and the Sn content decreased. Hence, a minimum κ_E of 0.15-0.19 Wm^-1K^-1 was achieved at 323-623 K in Cu₃Sb_0.94Sn_0.02Bi_0.04Se₄.

The κ_E values achieved in other studies were as follows: 0.18-0.17 Wm^-1K^-1 at 275-700 K for Cu₃Sb0.9Sn0.1Se₄ [5], 0.05-0.11 Wm^-1K^-1 at 323-575 K for Cu₃Sb0.7Bi0.3Se₄ [18], and 0.15-0.22 Wm^-1K^-1 at 323-673 K for Cu₃Sb_0.96Sn_0.02Bi_0.02Se₄ [13]. In this study, κ_L decreased as the temperature increased. When the Bi content was constant at 0.02, κ_L was lower as the Sn content increased; consequently, the lowest κ_L of 1.10-0.44 Wm^-1K^-1 was obtained at 323-623 K in Cu₃Sb_0.92Sn_0.06Bi_0.02Se₄. However, when the Bi content increased to 0.04, κ_L increased as the Sn content increased. Therefore, when the Bi doping level was low, the addition of Sn effectively reduced κ_L, whereas when the Sn doping level was low, the addition of Bi effectively reduced κ_E. Wei et al. [5] reported that the κ_L of all samples of Cu_2.95Sb_1-xSn_xSe₄ (x = 0.01-0.04) was 2.81-1.01 Wm^-1K^-1 at 275-700 K. Li et al. [18] obtained a minimum κ_L of 1.87-0.79Wm^-1K^-1 at 323-573 K for Cu₃Sb_0.97Bi_0.03Se₄. Liu et al. [13] achieved the lowest κ_L of 0.89-0.27 Wm^-1K^-1 at 323-673 K for Cu₃Sb_0.88Sn_0.1Bi_0.02Se₄.

Fig 8 shows the L of Cu₃Sb_1-x-ySn_xBi_ySe₄. Theoretically, the range of L is (1.45-2.44) × 10^-8 V²K^-2; higher numbers indicate degenerate semiconductor or metallic behavior, whereas smaller numbers indicate nondegenerate semiconductor behavior [21, 28]. A maximum L of (1.96-1.76) × 10^-8 V²K^-2 was obtained at 323-623 K in Cu₃Sb_0.92Sn_0.06Bi_0.02Se₄, whereas a minimum L of (1.79-1.64) × 10^-8 V²K^-2 was achieved at 323-623 K in Cu₃Sb_0.94Sn_0.02Bi_0.04Se₄. Sn doping increased L (shifted to the degenerate state); conversely, Bi doping decreased L (shifted to the nondegenerate state). Lee et al. [20] reported a L of (1.54-1.56) × 10^-8 V²K^-2 at 323-623 K for undoped Cu₃SbSe₄.

Fig. 8.

Temperature dependence of Lorenz number for Cu₃Sb_1-x-ySn_xBi_ySe₄.

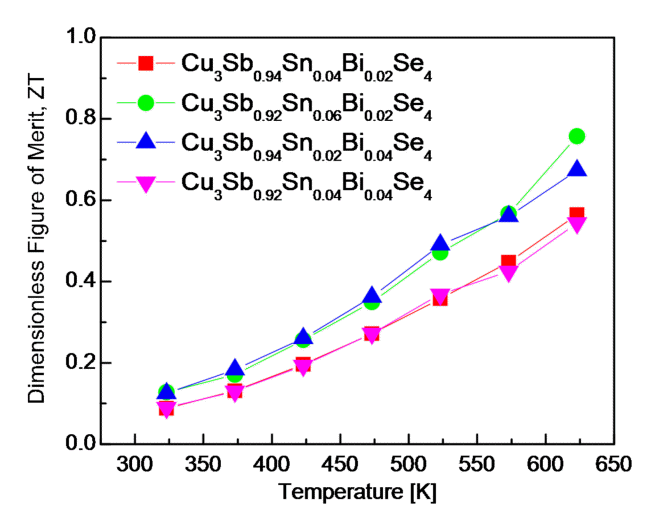
Fig 9 presents the ZT of Cu₃Sb_1-x-ySn_xBi_ySe₄. The highest ZT of 0.75 was obtained at 623 K in Cu₃Sb_0.92Sn_0.06Bi_0.02Se₄, the result of its high PF and low thermal conductivity. Although the thermal conductivity was the lowest when x = 0.02 and y = 0.04, the maximum ZT value was attributed to the highest PF, when x = 0.06 and y = 0.02. Lee et al. [20] reported a ZT of 0.39 at 623 K for undoped Cu₃SbSe₄, which was synthesized via the same process as ours; the reported ZT value was approximately two times higher than that achieved via Sn/Bi double doping. Wei et al. [5] reported a ZT of 0.70 at 673 K for Cu₃Sb_0.98Sn_0.02Se₄ synthesized via MA and spark plasma sintering (SPS). Li et al. [18] obtained a ZT of 0.70 at 600 K for Cu₃Sb_0.98Bi_0.02Se₄ synthesized via melting–SPS. Liu et al. [13] achieved an extremely high ZT of 1.26 at 673 K for Cu₃Sb_0.88Sn_0.10Bi_0.02Se₄ prepared via a multistep solution-based synthesis followed by HP; the thermal conductivity was approximately 1 Wm^-1K^-1, which was similar to our result, but the PF was 1.81 mWm^-1K^-2 (an anomalously high value for permingeatite), which was 1.4 times higher than ours (1.29 mWm^-1K^-2). These values were obtained because the carrier concentration was 1020cm^-3, which was two orders higher compared with that of our specimen. In addition to the doping level, the measured temperature of the thermoelectric properties was higher than 623 K, which contributed to the high ZT value because it was proportional to the measured temperature below the temperature at which the intrinsic transition and bipolar conduction occurred.

Fig. 9.

Dimensionless figure of merit for Cu₃Sb_1-x-ySn_xBi_ySe₄.

4. CONCLUSIONS

Permingeatite Cu₃Sb_1-x-ySn_xBi_ySe₄ (x = 0.02–0.06, y = 0.02–0.04) double-doped with Sn and Bi at the Sb site was synthesized via MA–HP. XRD analysis revealed that both the synthetic powders and sintered specimens investigated in this study were composed of a tetragonal permingeatite phase without secondary phases. All elements in the sintered samples were distributed uniformly, with a relative density of 97.7%–98.2%. After Sn and Bi were substituted at the Sb site, the lattice constant changed to 0.56510-0.56518 nm for the a-axis and 1.12509-1.12529 nm for the c-axis. The Hall and Seebeck coefficients were positive, thereby confirming that the Sn/Bi double-doped permingeatite is a p-type semiconductor. Sn doping resulted in charge compensation due to additional electrons; hence, the carrier concentration increased from 2.27 × 10¹⁶ to 2.74 × 10¹⁸ cm^-3, whereas the mobility decreased from 7.39 × 10⁴ to 1.88 × 10³ cm²Vs^-1. However, Bi doping did not significantly affect the charge transport properties. As the Sn content increased and the Bi content decreased, the electrical conductivity increased, where the highest electrical conductivity of (8.28-5.61) × 10⁴ Sm^-1 was exhibited at 323-623 K in Cu₃Sb_0.92Sn_0.06Bi_0.02Se₄. In contrast, as the Sn content decreased and the Bi content increased, the Seebeck coefficient increased, resulting in the highest Seebeck coefficient of 141-225 μVK^-1 at 323-623 K in Cu₃Sb_0.94Sn_0.02Bi_0.04Se₄. Consequently, Cu₃Sb_0.92Sn_0.06Bi_0.02Se₄ exhibited a maximum PF of (0.64-1.29) mWm^-1K^-2 at 323-623 K. Sn doping decreased the lattice thermal conductivity, whereas Bi doping reduced the electronic thermal conductivity but did not effectively reduce the lattice thermal conductivity. The lowest thermal conductivity of 1.40-0.91 Wm^-1K^-1 was obtained at 323-623 K in Cu₃Sb_0.94Sn_0.02Bi_0.04Se₄. Consequently, a maximum ZT of 0.75 was achieved at 623 K by Cu₃Sb_0.92Sn_0.06Bi_0.02Se₄.

Article information Continued