1. ņä£ ļĪĀ
ĻĖłņåŹĻ│ä ĒĢĀļØ╝ņØ┤ļō£ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ (metal-halide perovskites, MHPs)ļŖö ņĄ£ĻĘ╝ ļōżņ¢┤ Ļ░Ćņן ļ¦ÄņØĆ ņŻ╝ļ¬®ņØä ļ░øĻ│Ā ņ׳ļŖö ņ░©ņäĖļīĆ Ēā£ņ¢æņĀäņ¦Ć ņåīņ×¼ļØ╝ ĒĢĀ ņłś ņ׳ļŗż. 2009ļģä ņØ╝ļ│ĖņØś Miyasaka ĻĘĖļŻ╣ņØ┤ ņ▓śņØīņ£╝ļĪ£ methylammonium tri-iodide(MAPbI3)ļź╝ ņŚ╝ļŻīĻ░ÉņØæĒśĢ Ēā£ņ¢æņĀäņ¦ĆņØś Ļ┤æĒØĪņłśļ¼╝ņ¦łļĪ£ ņé¼ņÜ®ĒĢśņŚ¼ 3% ļīĆņØś Ļ┤æņĀäļ│ĆĒÖśĒÜ©ņ£©ņØä ĻĖ░ļĪØĒĢ£ ņØ┤Ēøä [1], ĒÅŁļ░£ņĀüņØĖ ĒÜ©ņ£©Ļ░£ņäĀņåŹļÅäļź╝ ļ│┤ņØ┤ļ®┤ņä£ ņĄ£ĻĘ╝ņŚÉļŖö 24% ņØ┤ņāüņØś Ļ│ĄņØĖ ĒÜ©ņ£©ņØä ĻĖ░ļĪØĒĢśņŚ¼ ļ░Ģļ¦ēĒśĢ Ēā£ņ¢æņĀäņ¦Ć Ēøäļ│┤ĻĄ░ ņżæ Ļ░Ćņן ļåÆņØĆ ĒÜ©ņ£©ņØä ĻĖ░ļĪØĒĢśĻ▓ī ļÉśņŚłļŗż [2]. ņØ┤ļ¤¼ĒĢ£ ĻĖēņåŹļÅäņØś ĒÜ©ņ£©Ļ░£ņäĀņØä ņ£äĒĢ┤, ņ¦Ćļé£ 9ļģäņŚ¼ ļÅÖņĢł ņłś ļ¦ÄņØĆ ņŚ░ĻĄ¼ņ×ÉļōżņØĆ ņåīņ×¼ ļ░Å Ļ│ĄņĀĢĻĖ░ņłĀņØś ņĄ£ņĀüĒÖöņÖĆ Ēā£ņ¢æņĀäņ¦ĆĻĄ¼ņĪ░ņØś Ļ░£ņäĀņØä ņ£äĒĢ┤ ļŗżņ¢æĒĢ£ ļģĖļĀźņØä Ļ▓ĮņŻ╝ĒĢ┤ ņÖöļŗż [3-5].
ņŚŁņé¼ņĀüņ£╝ļĪ£ ņ░ŠĻĖ░ Ēלļōż ņĀĢļÅäļĪ£ ļ╣ĀļźĖ ĒÜ©ņ£©ņØś Ļ░£ņäĀņåŹļÅäļź╝ ļ│┤ņØ╝ ņłś ņ׳ļŖö ņøÉņØĖņØä ņ░ŠĻĖ░ ņ£äĒĢ┤, ņĄ£ĻĘ╝ ļōżņ¢┤ ļŗżņ¢æĒĢ£ ņŗżĒŚś, ņĖĪņĀĢ ļ░Å Ļ│äņé░ņØä ĒåĄĒĢ┤ MHP ņ×¼ļŻīņØś ļÅģĒŖ╣ĒĢ£ ņä▒ņ¦łņØä ĻĘ£ļ¬ģĒĢśĻ│Āņ×É ĒĢśļŖö ņŗ£ļÅäĻ░Ć Ļ│äņåŹļÉśĻ│Ā ņ׳ļŗż. Ēśäņ×¼Ļ╣īņ¦Ć ļ░ØĒśĆņ¦ä ļ░öņŚÉ ļö░ļź┤ļ®┤ MHP ņ×¼ļŻīļŖö Ļ▓░ĒĢ©ĒŖ╣ņä▒ņØ┤ ļ¦żņÜ░ ļÅģĒŖ╣ĒĢśņŚ¼ ļé┤ņ×¼Ļ▓░ĒĢ©ņŚÉ ņØśĒĢ£ charge trappingņØ┤ ļ░£ņāØĒĢśņ¦Ć ņĢŖļŖö Ļ▓āņ£╝ļĪ£ ņĢīļĀżņĪīļŗż [6]. ļśÉĒĢ£ MAPbI3ņØś Ļ▓ĮņÜ░ Rashba ĒÜ©Ļ│╝ļĪ£ ņØĖĒĢ┤ ņåīņ×¼ ļé┤ļČĆņŚÉņä£ņØś recombinationņØ┤ ņ¢ĄņĀ£ļÉśĻ│Ā ņ׳ļŗż [7]. ņĀĆļĀ┤ĒĢ£ ņÜ®ņĢĪĻ│ĄņĀĢņ£╝ļĪ£ ņĀ£ņĪ░ĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ ņåīņ×¼ ļé┤ļČĆņŚÉļŖö ļŗżņ¢æĒĢ£ ĒśĢĒā£ņØś Ļ▓░ĒĢ©ņØś ņĪ┤ņ×¼ļź╝ Ēö╝ĒĢĀ ņłś ņŚåņØīņŚÉļÅä ļČłĻĄ¼ĒĢśĻ│Ā ņØ┤ļ¤¼ĒĢ£ MHPņåīņ×¼ņØś ĒŖ╣ņłśņä▒ņ£╝ļĪ£ ņØĖĒĢ┤ ņ¦äĻ│ĄĻ│ĄņĀĢņØä ĒåĄĒĢ┤ ņĀ£ņĪ░ļÉśļŖö ĻĖ░ņĪ┤ņØś ļ░Ģļ¦ēĒśĢ Ēā£ņ¢æņĀäņ¦ĆņÖĆ Ļ▓Įņ¤üĒĢĀ ņłś ņ׳ļŖö ĒÜ©ņ£©ņØä ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗżĻ│Ā ĒĢĀ ņłś ņ׳ļŗż.
ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ Ēā£ņ¢æņĀäņ¦ĆņØś ĻĄ¼ņĪ░ļŖö ņĀäĒĢśņłśņåĪņĖĄņØä ņĀüņĖĄĒĢśļŖö ņł£ņä£ņŚÉ ļö░ļØ╝, normal type (n-i-p) Ļ│╝ inverted type (p-i-n) ņ£╝ļĪ£ ļéśļłī ņłś ņ׳ļŗż. Ēśäņ×¼ ņĄ£Ļ│ĀĒÜ©ņ£©ņØś Ēā£ņ¢æņĀäņ¦ĆļŖö n-i-p ĻĄ¼ņĪ░ļź╝ ĒåĄĒĢ┤ ĻĄ¼ĒśäļÉśĻ│Ā ņ׳ļŖöļŹ░, p-i-n ĻĄ¼ņĪ░ļŖö n-i-p ĻĄ¼ņĪ░ņŚÉ ļ╣äĒĢ┤ ĒÜ©ņ£© ņĖĪļ®┤ņŚÉņä£ļŖö ņĢĮĻ░ä ļé«ņØĆ Ļ░ÆņØä ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ņ£╝ļéś, hysteresis Ļ░Ć ņĀüĻ▓ī ļ░£ņāØĒĢśļ®░ [8,9], Si Ēā£ņ¢æņĀäņ¦ĆņÖĆ tandem ĻĄ¼ņĪ░ļź╝ ļ¦īļōżĻĖ░ņŚÉ ņÜ®ņØ┤ĒĢśļŗżļŖö ņןņĀÉņ£╝ļĪ£ ņØĖĒĢ┤ ņ¦ĆņåŹņĀüņØĖ Ļ┤Ćņŗ¼ņØä ļ░øĻ│Ā ņ׳ļŗż [10,11]. Inverted type Ēā£ņ¢æņĀäņ¦ĆņŚÉņä£ļŖö ņĀĢĻ│ĄņłśņåĪņĖĄņØ┤ ļ╣øņØä ĒØĪņłśĒĢśļŖö ļ░®Ē¢źņŚÉ ņĪ┤ņ×¼ĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ, ņĀĢĻ│ĄņłśņåĪņĖĄ(hole transport layers, HTLs) [12] Ļ│╝ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖņĖĄņØä ļÅÖņŗ£ņŚÉ ņĄ£ņĀüĒÖöĒĢśļŖö Ļ▓āņØ┤ ĒĢäņłśņĀüņØ┤ļŗż. Ēśäņ×¼ inverted typeņŚÉņä£ HTLļĪ£ ļ¦ÄņØ┤ ĒÖ£ņÜ®ļÉśļŖö ļ¼╝ņ¦łļĪ£ļŖö Nickel Oxide (NiOx) [13,14], Poly(3,4-ethylenedioxythiophene) Polystyrene Sulfonate (PEDOT:PSS) [8], Copper Thiocyanate (CuSCN) [15,16], Copper Iodide (CuI) [16] ļź╝ ļōż ņłś ņ׳ļŗż. ņØ┤ ļōż Ļ░üĻ░üņØś HTL ļ¼╝ņ¦łļōżņØĆ ņä£ļĪ£ ļŗżļźĖ Ļ┤æņĀäĻĖ░ņĀü ļ¼╝ņä▒ņØä Ļ░¢Ļ│Ā ņ׳ĻĖ░ ļĢīļ¼ĖņŚÉ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖņÖĆ Ļ░ÖņØ┤ ņĀüņĖĄĒĢśņśĆņØä ļĢī ņĄ£ņĀüņØś ļæÉĻ╗ś ļ░Å ņĄ£Ļ│ĀĻĖ░ļīĆĒÜ©ņ£©ņØ┤ ļŗ¼ļØ╝ņ¦ł ņłś ņ׳ļŗż. ņÜ®ņĢĪĻ│ĄņĀĢņ£╝ļĪ£ ļ░Ģļ¦ēņØä ņĀ£ņĪ░ĒĢśļŖö ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ Ēā£ņ¢æņĀäņ¦ĆņØś ĒŖ╣ņä▒ņāü, ņåīņ×ÉņØś ĻĄ¼ņĪ░ ļ░Å ņåīņ×¼ņØś ĒŖ╣ņä▒ņØĆ ņĀ£ņĪ░ĒĢśļŖö ņŚ░ĻĄ¼ņ×ÉņØś ņłÖļĀ©ļÅäņÖĆ Ļ│ĄņĀĢļ░®ļ▓ĢņŚÉ ņØśĒĢ┤ ļ¦ÄņØĆ ĒÄĖņ░©ļź╝ Ļ░¢Ļ▓ī ļÉ£ļŗż. ņØ┤ļ¤¼ĒĢ£ ņŗżĒŚśņāüņØś ĒÄĖņ░©ļĪ£ ņØĖĒĢ┤ ņĄ£Ļ│Ā ĒÜ©ņ£©ņØä ļÅäņČ£ĒĢĀ ņłś ņ׳ļŖö ļ░Ģļ¦ēļ¼╝ņ¦ł ļ░Å ĻĄ¼ņĪ░ņØś Ļ▓░ņĀĢņØĆ ņŗżĒŚśņĀüņØĖ ļ░®ļ▓Ģļ¦īņ£╝ļĪ£ļŖö ņ¢┤ļĀĄļŗżĻ│Ā ĒĢĀ ņłś ņ׳ļŗż.
ļ░śļÅäņ▓┤ņØś ņĀäĒĢśņłśņåĪņØä ĒĢ┤ņäØĒĢśļŖö Ļ│äņé░ļ░®ļ▓ĢņØĆ ļ░śļÅäņ▓┤ņåīņ×¼ļĪ£ļČĆĒä░ ņØ┤ļüīņ¢┤ ļé╝ ņłś ņ׳ļŖö ņØ┤ņāüņĀüņØĖ ĒÜ©ņ£©ņØä ņśłņĖĪĒĢĀ ņłś ņ׳ļŗż. ĻĖłņåŹĻ│ä ĒĢĀļØ╝ņØ┤ļō£ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ ļ¼╝ņ¦ł ņŚŁņŗ£ ļ╣øņØä ĒØĪņłśļŖö ļ¼╝ļĪĀ ņĀäĒĢśņłśņåĪņØ┤ Ļ░ĆļŖźĒĢ£ ļ░śļÅäņ▓┤ ļ¼╝ņ¦łņ×äņØ┤ ļ░ØĒśĆņ¦ä ņØ┤Ēøä [4], ļ░śļÅäņ▓┤ Ēā£ņ¢æņĀäņ¦Ćļź╝ ĒĢ┤ņäØĒĢśļŖö ļŹ░ ņé¼ņÜ®Ļ░ĆļŖźĒĢ£ ņŗ£ļ«¼ļĀłņØ┤ņģś ĻĖ░ļ▓ĢņØä ĒÖ£ņÜ®ĒĢ£ ņŚ░ĻĄ¼Ļ░Ć ĒÖ£ļ░£Ē׳ ņ¦äĒ¢ēļÉśņŚłļŗż. Liu ļō▒ņØ┤ 2014ļģäņŚÉ ļ░£Ēæ£ĒĢ£ planar-type ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ Ēā£ņ¢æņĀäņ¦ĆņØś ĻĖ░ļīĆĒÜ©ņ£© ņśłņĖĪņŚÉ ļīĆĒĢ£ Ļ│äņé░ļģ╝ļ¼Ė [17]ņØ┤ ļ░£Ēæ£ļÉ£ ņØ┤Ēøä, Ēā£ņ¢æņĀäņ¦ĆņØś Ļ▒░ļÅÖņŚÉ ļ»Ėņ╣śļŖö ņåīņ×¼ņØś ņśüĒ¢źņØä ĒīīņĢģĒĢśĻ│Ā ĻĄ¼ņĪ░ļź╝ ņĄ£ņĀüĒÖöĒĢśļŖö ļ░®ļ▓ĢņŚÉ ļīĆĒĢ£ ļ░£Ēæ£Ļ░Ć Ļ│äņåŹļÉśņ¢┤ ņÖöļŗż [18-20].
ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ Ēā£ņ¢æņĀäņ¦ĆņØś ņĄ£ņĀü ņĀäĒĢśņłśņåĪņĖĄņØä ļÅäņČ£ĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö, ļŗżņ¢æĒĢ£ Ēøäļ│┤ĻĄ░ ļ¼╝ņ¦łņŚÉ ļīĆĒĢśņŚ¼, Ēā£ņ¢æņĀäņ¦Ć ļ░Ģļ¦ēņĖĄņØś ļæÉĻ╗śļź╝ ņĄ£ņĀüĒÖöĒĢśļŖö Ļ│╝ņĀĢņØä Ļ▒░ņ│ÉņĢ╝ ĒĢ£ļŗż. Ļ░ü ņĀĢĻ│ĄņłśņåĪņĖĄņØĆ Ļ░üĻĖ░ ļŗżļźĖ ņĀäņ×ÉĻĄ¼ņĪ░ņÖĆ ĻĄ┤ņĀłļźĀņØä Ļ░¢Ļ│Ā ņ׳ĻĖ░ ļĢīļ¼ĖņŚÉ, ļŗ¼ņä▒Ļ░ĆļŖźĒĢ£ ņĄ£Ļ│ĀĒÜ©ņ£©Ļ│╝ ņĄ£ņĀüņØś ĻĄ¼ņĪ░ļŖö Ļ░ü ļ¼╝ņ¦łņŚÉ ļö░ļØ╝ ļŗżļź╝ ņłśļ░¢ņŚÉ ņŚåļŗż. ņóģļלņØś ņŗ£ļ«¼ļĀłņØ┤ņģś ņŚ░ĻĄ¼ļōżņØĆ ļ¼╝ņ¦łņØś ļ│ĆĒÖöļŖö Ļ│ĀļĀżĒĢśņ¦Ć ņĢŖĻ│Ā, ĻĄ¼ņĪ░ņØś ļ│ĆĒÖöļ¦īņØä Ļ│ĀļĀżĒĢśĻ▒░ļéś ļ░Ģļ¦ē ļæÉĻ╗śļŖö Ļ│ĀņĀĢĒĢ£ ņ▒äļĪ£ ļ¼╝ņ¦łņØś ļ│ĆĒÖöļ¦īņØä ĒāÉĻĄ¼ĒĢśņśĆĻĖ░ ļĢīļ¼ĖņŚÉ, ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ Ēā£ņ¢æņĀäņ¦ĆņØś ņĄ£Ļ│Āņä▒ļŖźņØä ņ£äĒĢ£ ņ×¼ļŻīņØś ļÅäņČ£ņŚÉļŖö ņ¢┤ļĀżņøĆņØ┤ ņ׳ņŚłļŗż. ĻĘĖļ”¼Ļ│Ā, ĻĄ¼ņĪ░ļ│ĆĒÖöņŚÉ ļö░ļźĖ ņé░ĒżļŖö ņóģļלņŚ░ĻĄ¼ņŚÉņä£ Ļ│ĀļĀżļÉśņ¦Ć ņĢŖĻ│Ā ņ׳ļŖöļŹ░, ņÜ®ņĢĪĻ│ĄņĀĢņ£╝ļĪ£ ņĀ£ņĪ░ĒĢśļŖö ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ Ēā£ņ¢æņĀäņ¦ĆņØś ĒŖ╣ņä▒ņāü ņé░ĒżņØś ņ¢ĄņĀ£ļŖö Ļ░Ćņן ņżæņÜöĒĢ£ ņäżĻ│äņØĖņ×ÉļØ╝ ĒĢĀ ņłś ņ׳ļŗż.
ļö░ļØ╝ņä£, ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ Ēā£ņ¢æņĀäņ¦Ćļź╝ ĻĄ¼ņä▒ĒĢśļŖö ņĀĢĻ│ĄņłśņåĪņĖĄņØś ļ¼╝ņ¦łĻ│╝ ĻĄ¼ņĪ░ ļæÉ Ļ░Ćņ¦Ć ņĖĪļ®┤ņØä ļ¬©ļæÉ Ļ│ĀļĀżĒĢ£ ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ĒåĄĒĢ┤, ņé░Ēżļź╝ ņĄ£ļīĆļĪ£ ņ¢ĄņĀ£ĒĢśļ®░ ņĄ£Ļ│ĀņØś ņä▒ļŖźņØä ļé╝ ņłś ņ׳ļŖö ņĀĢĻ│ĄņłśņåĪņĖĄ ļ¼╝ņ¦łĻ│╝ ĻĄ¼ņĪ░ļź╝ ņĀ£ņĢłĒĢśĻ│Āņ×É ĒĢ£ļŗż. ņÜ░ņäĀ Ļ│äņé░ņŚÉ ĒÖ£ņÜ®ļÉ£ ņłśĒĢÖņĀü ļ░®ļ▓ĢņØä Ļ░äļץĒ׳ ņåīĻ░£ĒĢ£ļŗż. ĻĘĖ ļŗżņØī ņĀäĒĢśņłśņåĪņĖĄ ļ¼╝ņ¦łņØś ļ│ĆĒÖöņÖĆ Ēā£ņ¢æņĀäņ¦ĆņØś Ļ▒░ļÅÖņ¢æņāüņØś ņāüĻ┤ĆĻ┤ĆĻ│äļź╝ ļČäņäØĒĢśņŚ¼ ņĀĢĻ│ĄņłśņåĪņĖĄ ļ¼╝ņ¦łņØś ņśüĒ¢źņØä Ļ│Āņ░░ĒĢ£ļŗż. ļŗżņØīņ£╝ļĪ£ ļ░Ģļ¦ēņØś ļæÉĻ╗śņØś ļ│ĆĒÖöĻ░Ć ĒÜ©ņ£© ļ░Å ņåīņ×É ĒŖ╣ņä▒ņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņØä ļ¼╝ņ¦łļ│äļĪ£ ļÅäņČ£ĒĢśņŚ¼ ņĄ£ņĀüņØś ļ¼╝ņ¦łĻ│╝ ĻĄ¼ņĪ░ļź╝ ļÅäņČ£ĒĢśĻ│Ā, ņØ┤ļź╝ ļ░öĒāĢņ£╝ļĪ£ Ļ░ü ņĀĢĻ│ĄņĀäļŗ¼ ļ¼╝ņ¦łņØ┤ Ēā£ņ¢æņĀäņ¦ĆņØś ĒÜ©ņ£©ņØś ņé░ĒżņŚÉ ĻĖ░ņŚ¼ĒĢśļŖö ņ¢æņØä ņĀĢļ¤ēĒÖöĒĢśņŚ¼ ļÅäņČ£ĒĢśĻ│Āņ×É ĒĢ£ļŗż.
2. Ļ│äņé░ ļ░®ļ▓Ģ
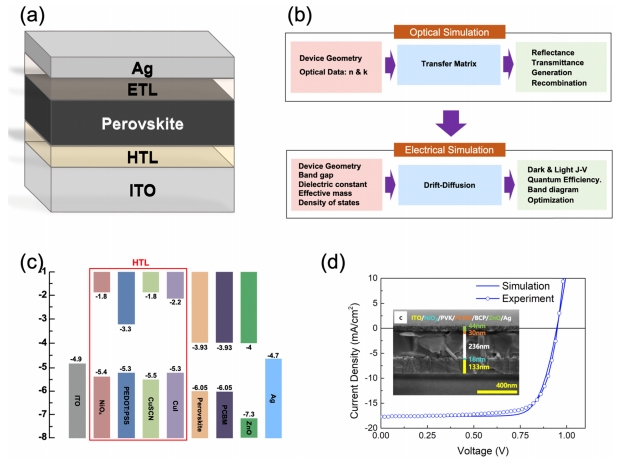
ļ│Ė ņŚ░ĻĄ¼ņŚÉ ņé¼ņÜ®ĒĢ£ inverted typeņØś ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ Ēā£ņ¢æņĀäņ¦ĆĻĄ¼ņĪ░ņØś Ļ░£ļץļÅäļź╝ ĻĘĖļ”╝ 1(a)ņŚÉ ļÅäņŗ£ĒĢśņśĆļŗż. ļ╣øņØ┤ ļōżņ¢┤ņśżļŖö ņ¬ĮņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö ITOņØś ļæÉĻ╗śļŖö 200 nmļĪ£ ņäżņĀĢĒĢśņśĆĻ│Ā, ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖņÖĆ ņĀĢĻ│ĄņłśņåĪņĖĄ (hole transport layer, HTL)ņØś ļæÉĻ╗śļŖö 100 nm ~ 600 nm, 20 nm ~ 220 nm ļĪ£ ļŗżņ¢æĒĢśĻ▓ī ļ│ĆĒÖöņŗ£ņ╝£Ļ░Ćļ®┤ņä£ Ļ│äņé░ņØä ņłśĒ¢ēĒ¢łļŗż. ņĀäņ×ÉņłśņåĪņĖĄ (electron transport layer, ETL) Ļ│╝ top-electrodeļŖö PCBMĻ│╝ Agļź╝ ĻĖ░ņżĆļ¼╝ņ¦łļĪ£ ņé¼ņÜ®ĒĢśņśĆņ£╝ļ®░, ņĀÉĻ▓Ć Ļ▓░Ļ│╝ ņØ┤ ļæÉ ņĖĄņØś ļæÉĻ╗śļŖö inverted type Ēā£ņ¢æņĀäņ¦ĆņØś Ļ▒░ļÅÖņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņØ┤ ļ»Ėļ»ĖĒĢśņśĆļŗż. ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖļŖö Ļ░Ćņן ļäÉļ”¼ ņé¼ņÜ®ļÉśĻ│Ā ņ׳ļŖö MAPbI3ļź╝ ĒĢ┤ņäØ ļīĆņāüņ£╝ļĪ£ ĒĢśņśĆņ£╝ļ®░ ļ¼╝ņä▒ņØĆ Liu ļō▒ņØ┤ ļ░£Ēæ£ĒĢ£ ņØ┤ņĀä ļģ╝ļ¼ĖņŚÉ ņ׳ļŖö ļ¼╝ņä▒ņ╣śļź╝ ņé¼ņÜ®ĒĢśņśĆĻ│Ā [17], MAPbI3 ņØś complex refractive indexļŖö Xing ļō▒ņØ┤ ļ░£Ēæ£ĒĢ£ ļģ╝ļ¼ĖņØś Ļ░ÆņØä ņČöņČ£ĒĢśņŚ¼ ņé¼ņÜ®ĒĢśņśĆļŗż [21].
Ēā£ņ¢æņĀäņ¦ĆņØś ņŚäļ░ĆĒĢ£ ĒĢ┤ņäØņØä ņ£äĒĢ┤ņä£ļŖö Ļ┤æĒĢÖĻ│äņé░Ļ│╝ [22] ļ░śļÅäņ▓┤ņłśņåĪļ¬©ļŹĖņØä Ļ▓░ĒĢ®ĒĢ£ ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢ┤ņĢ╝ ĒĢ£ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņØ┤ņÖĆ Ļ░ÖņØĆ Ļ┤æĒĢÖ-ļ░śļÅäņ▓┤ņłśņåĪ Ļ▓░ĒĢ®Ļ│äņé░ņØä ņ£äĒĢśņŚ¼ Synopsysņé¼ņØś Synopsys-TCAD [23]ļź╝ ĒÖ£ņÜ®ĒĢśņŚ¼ Ļ│äņé░ņØä ņłśĒ¢ēĒĢśņśĆļŗż. ņŗ£ļ«¼ļĀłņØ┤ņģś Ļ│╝ņĀĢņØä ĻĘĖļ”╝ 1(b)ņŚÉ ļéśĒāĆļé┤ņŚłļŗż. ļ╣øņØś ņĪ░ņé¼ņŚÉ ņØśĒĢ£ ņĀäĒĢśņØś ņāØņä▒ņØĆ ņĀäņ×Éņåīņ×ÉņØś ņĀäĒĢśņØś ņøĆņ¦üņ×äņŚÉ ļ╣äĒĢ┤ ņāüļīĆņĀüņ£╝ļĪ£ ļ╣Āļź┤ĻĖ░ ļĢīļ¼ĖņŚÉ, ļ│Ė Ļ│äņé░ņŚÉņä£ļŖö Ļ┤æĒĢÖĻ│äņé░ņØä ņÜ░ņäĀņĀüņ£╝ļĪ£ ņłśĒ¢ēĒĢśĻ│Ā ņŚ¼ĻĖ░ņä£ ļÅäņČ£ļÉ£ Ļ┤æņāØņä▒ ņĀäļźśļČäņØä ļ░śļÅäņ▓┤ ņłśņåĪļ¬©ļŹĖņØś source ĒĢŁņŚÉ ļŹöĒĢ┤ņä£ Ļ│äņé░ņØä ņłśĒ¢ēĒĢśļŖö Ļ│äņĖĄņĀü ņŚ░Ļ▓░ĒĢ┤ņäØ ļ░®ļ▓ĢņØä ņé¼ņÜ®ĒĢ£ļŗż. ņĪ░ĻĖł ļŹö ņāüņäĖĒĢśĻ▓ī ĻĖ░ņłĀĒĢśļ®┤ ļŗżņØīĻ│╝ Ļ░Öļŗż. ņåīņ×Éļź╝ ĻĄ¼ņä▒ĒĢśĻ│Ā ņ׳ļŖö ļ¼╝ņ¦łņØś ĻĄ¼ņĪ░ ļ░Å ĒīīņןņŚÉ ļö░ļźĖ ĻĄ┤ņĀłļźĀ, ĒØĪņłśĻ│äņłśļź╝ ļ¼╝ņ¦łņāüņłśĻ░Æņ£╝ļĪ£ ņ×ģļĀźĒĢśņŚ¼ transfer matrix method (TMM)ļź╝ ņé¼ņÜ®ĒĢ£ Ļ┤æĒĢÖĻ│äņé░ņØä ņłśĒ¢ēĒĢ£ļŗż. TMM Ļ│äņé░ņØä ĒåĄĒĢ┤ Ēā£ņ¢æņĀäņ¦ĆĻĄ¼ņĪ░ņŚÉņä£ Ļ░ü ņ£äņ╣śļ│ä ļ░śņé¼ņ£©, Ēł¼Ļ│╝ņ£©, ĒØĪņłśņ£©ņØ┤ ļÅäņČ£ļÉśļ®░, ņŻ╝ņ¢┤ņ¦ä Ēā£ņ¢æĻ┤æ ņŖżĒÄÖĒŖĖļ¤╝ Ļ░ÆņŚÉ ĒØĪņłśņ£©ņØä Ļ│▒ĒĢśņŚ¼ Ļ░ü Ļ│äņé░Ļ▓®ņ×ÉņĀÉ ļ│äļĪ£ ņĀäĒĢśņØś ņāØņä▒ļČäņØä Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż. ņØ┤ļĀćĻ▓ī ļÅäņČ£ļÉ£ Ļ┤æņĀäĒĢś ņāØņä▒ļČäņØä ļ░śļÅäņ▓┤ ņłśņåĪļ¬©ļŹĖņØś ņĀäĒĢśņāØņä▒ĒĢŁņŚÉ ļŹöĒĢ┤ ņŻ╝Ļ▓ī ļÉ£ļŗż. ļ░śļÅäņ▓┤ ņłśņåĪļ¬©ļŹĖļĪ£ļŖö drift-diffusion (DD) ļ¬©ļŹĖņØä ņé¼ņÜ®ĒĢśņśĆļŗż [24]. DD ļ¬©ļŹĖņŚÉņä£ļŖö ņĀäņ×ÉņÖĆ ņĀĢĻ│ĄņØś ņŚ░ņåŹļ░®ņĀĢņŗØ (ņŗØ (1)Ļ│╝ (2)) Ļ│╝ ņĀäņ£äņ░©ņŚÉ ļīĆĒĢ£ Poisson ņŗØ (ņŗØ(3))ņØä ļÅÖņŗ£ņŚÉ ņłśļĀ┤ņŗ£ņ╝£ņä£ ņĀäņ£äĻ░ÆĻ│╝ ņĀäļźśĻ░ÆņØä ļÅäņČ£ĒĢśĻ▓ī ļÉśļŖöļŹ░, ņØ┤ ļĢī ņĢ×ņäĀ Ļ┤æĒĢÖĻ│äņé░ņŚÉņä£ ļÅäņČ£ļÉ£ Ļ┤æņĀäĒĢś ņāØņä▒ĒĢŁĻ│╝, ļ░śļÅäņ▓┤ ņłśņåĪļ¬©ļŹĖņØś ņ×¼Ļ▓░ĒĢ®ļ¬©ļŹĖ (direct recombination, indirect recombination, SRH recombination model)ņØä Ļ▓░ĒĢ®ĒĢśņŚ¼ ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśĻ▓ī ļÉ£ļŗż.
ņ£ä ņŗØņŚÉņä£ n, p, qļŖö Ļ░üĻ░ü ņĀäņ×É, ņĀĢĻ│ĄņØś ļåŹļÅäņÖĆ ņĀäĒĢśņØś ĻĖ░ņżĆņ╣śļź╝ ņØśļ»ĖĒĢśļ®░, Un Ļ│╝ Up ļŖö ņĀäņ×ÉņÖĆ ņĀĢĻ│ĄņØś ņāØņä▒-ņ×¼Ļ▓░ĒĢ® ļČäņ£©ņØ┤ļŗż. NDņÖĆ NAļŖö ņØ┤ņś©ĒÖöļÉśņ¢┤ ņ׳ļŖö donorņÖĆ acceptorņØś ļåŹļÅä Ļ░ÆņØ┤ļ®░ Jn Ļ│╝ Jp ļŖö ņĀäņ×ÉņÖĆ ņĀĢĻ│ĄņØś ņĀäļźśļ░ĆļÅäļź╝ ņØśļ»ĖĒĢśļ®░, ņŗØ (4) ņÖĆ (5)ņŚÉ ļéśĒāĆļé£ Ļ▓āņ▓śļ¤╝ ņĀäĒĢśņØś driftņÖĆ diffusion ĒĢŁņ£╝ļĪ£ ĻĄ¼ņä▒ļÉśņ¢┤ ņ׳ļŗż.
E ļŖö ņĀäĻĖ░ņןņØś ņäĖĻĖ░ņØ┤ļ®░, ╬╝ Ļ│╝ D ļŖö Ļ░üĻ░ü ņĀäĒĢśņØś ņØ┤ļÅÖļÅäņÖĆ ĒÖĢņé░Ļ│äņłśļź╝ Ļ░üĻ░ü ņØśļ»ĖĒĢ£ļŗż. DDMņØä ņé¼ņÜ®ĒĢ£ ļ░śļÅäņ▓┤ ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ņłśĒ¢ēĒĢĀ ļĢī ņØ┤ņóģņĀæĒĢ®Ļ░ä Ļ│äļ®┤ņŚÉņä£ļŖö conduction band (CB)ņÖĆ valence band (VB)ņØś ļ░░ņŚ┤ņØ┤ ļ¦żņÜ░ ņżæņÜöĒĢśļŗż [25]. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ Ļ│ĀļĀżĒĢ£ 4Ļ░Ćņ¦Ć HTL ļ¼╝ņ¦łņØś CB ļ░Å VBņØś ļ░░ņŚ┤ņØä ĻĘĖļ”╝ 1(c)ņŚÉ ļÅäņŗ£ĒĢśņśĆļŗż. HTLļĪ£ ĻĖ░ļŖźĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ņĀĢĻ│ĄņØś ņłśņåĪņØĆ ņøÉĒÖ£ĒĢśĻ▓ī ņØ╝ņ¢┤ļéśļ®┤ņä£ ņĀäņ×ÉņŚÉ ļīĆĒĢ┤ņä£ļŖö ņŚÉļäłņ¦Ćņןļ▓ĮņØś ņŚŁĒĢĀņØä ņłśĒ¢ēĒĢ┤ņĢ╝ ĒĢśļŖöļŹ░, ĻĘĖļ”╝ņŚÉ ļÅäņŗ£ļÉ£ Ļ▓āņ▓śļ¤╝ 4Ļ░Ćņ¦Ć ļ¼╝ņ¦ł ļ¬©ļæÉ ĒĢ┤ļŗ╣ ĻĖ░ļŖźņØä ņłśĒ¢ēĒĢśļŖö ļŹ░ ņ¦ĆņןņØ┤ ņŚåņØä Ļ▓āņ£╝ļĪ£ ņśłņāüļÉ£ļŗż. Ļ│äņé░ņŚÉ ņé¼ņÜ®ļÉ£ NiOx, PEDOT:PSS, CuSCNĻ│╝ CuIņØś ļ¼╝ņä▒ņØä Ēæ£ 1ņŚÉ ņĀĢļ”¼ĒĢśņśĆļŗż. Ļ░£ļ░£ļÉ£ Ļ│äņé░ļ¬©ļōłņØś ņĀüņÜ®Ļ░ĆļŖźņä▒ņØä Ļ▓Ćņ”ØĒĢśĻĖ░ ņ£äĒĢ┤ ļ│Ė ĻĘĖļŻ╣ņØ┤ ņĀ£ņĪ░ĒĢ£ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ Ēā£ņ¢æņĀäņ¦ĆņØś ĻĄ¼ņĪ░ņŚÉ ņĀüņÜ®ĒĢśņŚ¼ ņ¦üļĀ¼ņĀĆĒĢŁĻ│╝ Ļ▓░ĒĢ© ļåŹļÅäņØś ļ│ĆĒÖöļź╝ ĒåĄĒĢ┤ ņŗżĒŚśĻ▓░Ļ│╝ļź╝ ļ░śņśüĒĢĀ ņłś ņ׳ļŖö Ļ▓░Ļ│╝Ļ░Ć ļÅäņČ£ļÉ©ņØä ĒÖĢņØĖĒĢśņśĆļŗż. (ĻĘĖļ”╝ 1(d))
3. Ļ▓░Ļ│╝ ļ░Å Ļ│Āņ░░
3.1. ņĀĢĻ│ĄņłśņåĪņĖĄ ļ¼╝ņ¦łĻ│╝ Ēā£ņ¢æņĀäņ¦Ćņä▒ļŖźņØś ņāüĻ┤ĆĻ┤ĆĻ│ä
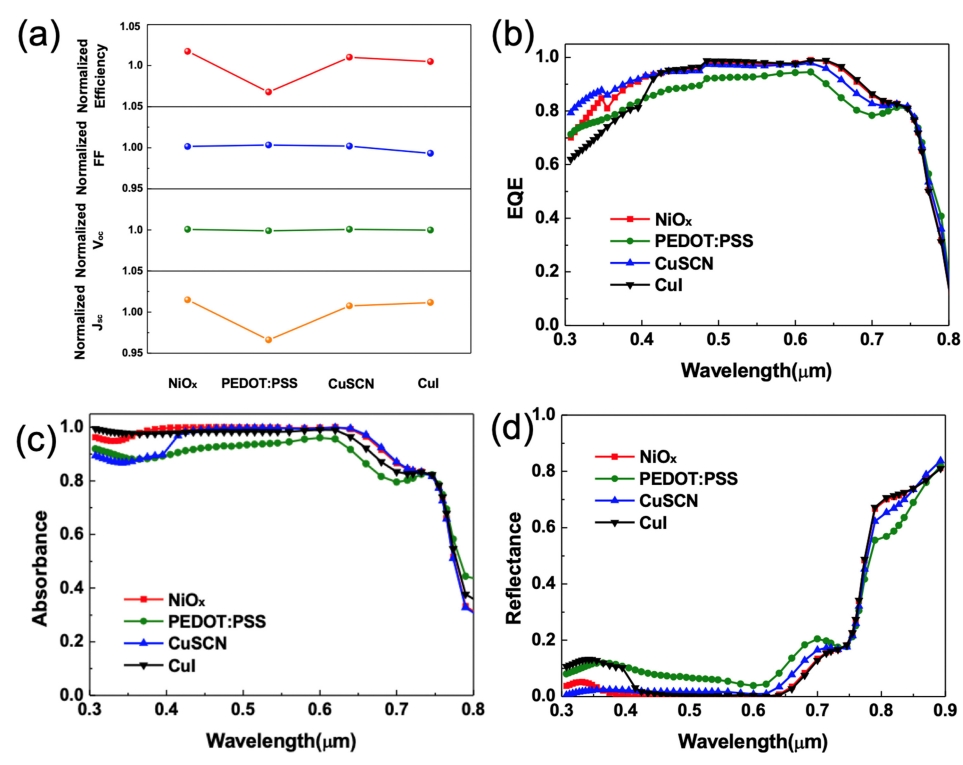
ņĀĢĻ│ĄņłśņåĪņĖĄņØ┤ Ēā£ņ¢æņĀäņ¦Ć Ļ▒░ļÅÖņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņØä ļČäņäØĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ļÅÖņØ╝ĒĢ£ Ēā£ņ¢æņĀäņ¦ĆĻĄ¼ņĪ░ļź╝ ĒśĢņä▒ĒĢśĻ│Ā, ņĀĢĻ│ĄņłśņåĪļ¼╝ņ¦łņØä ļŗ¼ļ”¼ĒĢśņŚ¼ Ēā£ņ¢æņĀäņ¦Ć ņä▒ļŖźĒÅēĻ░ĆņØś ņŻ╝ņÜöņØĖņ×ÉņØĖ, Ļ┤æņĀäļ│ĆĒÖśĒÜ©ņ£©(power conversion efficiency, PCE), fill factor (FF), ļŗ©ļØĮņĀäļźś (short circuit current, JSC), ĻĘĖļ”¼Ļ│Ā Ļ░£ļ░®ņĀäņĢĢ(open circuit voltage, VOC) ļź╝ Ļ│äņé░ĒĢ£ Ļ▓░Ļ│╝ļź╝ Ēæ£ 2ņŚÉ ļéśĒāĆļé┤ņŚłļŗż. ĻĖ░ņżĆ ņĪ░Ļ▒┤ņ£╝ļĪ£ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖņØś ļæÉĻ╗śļź╝ 350 nm, ņĀĢĻ│ĄņłśņåĪņĖĄņØś ļæÉĻ╗ś 30 nm ļĪ£ ņäżņĀĢĒĢśņŚ¼ Ļ│äņé░ņØä ņłśĒ¢ēĒĢśņśĆļŗż. ĒÜ©ņ£©ņØä ļ│┤ļ®┤ NiOxĻ░Ć 23.02%ļĪ£ Ļ░Ćņן ļåÆņĢśĻ│Ā, ĻĘĖ ļŗżņØīņ£╝ļĪ£ CuSCNņØ┤ 22.86%, CuIĻ░Ć 22.45%, ļ¦łņ¦Ćļ¦ēņ£╝ļĪ£ PEDOT:PSSĻ░Ć 21.9%ļĪ£ Ļ░Ćņן ļé«ņĢśļŗż. ļ╣äĻĄÉņØś ĒÄĖņØśļź╝ ņ£äĒĢ┤ CuSCNņØś Ļ░ÆņØä ĻĖ░ņżĆņ£╝ļĪ£ ĒĢśņŚ¼ Ļ░ü Ēā£ņ¢æņĀäņ¦ĆņØś ņä▒ļŖźĻ░ÆņØä normalizeĒĢśņŚ¼ ĻĘĖļ”╝ 2ņŚÉ ļÅäņŗ£ĒĢśņśĆļŗż. VOCļŖö 1.21 V ļĪ£ ļÅÖņØ╝ĒĢ£ ņłśņżĆņØ┤ņŚłĻ│Ā, FF ļśÉĒĢ£ ņĢĮ 86%ļĪ£ Ļ▒░ņØś ņ░©ņØ┤Ļ░Ć ņŚåņŚłļŗż. Ļ░Ćņן ņ░©ņØ┤Ļ░Ć Ēü░ ņÜöņØĖņØĆ JSC ņśĆļŗż. NiOxņÖĆ CuSCN, CuIļŖö 21.85~22.01 mA/cm2ņ£╝ļĪ£ ļ╣äņŖĘĒĢ£ ņłśņżĆņØ┤ņŚłņ¦Ćļ¦ī PEDOT:PSSļŖö 20.95 mA/cm2 ņ£╝ļĪ£ Ļ░Ćņן ļé«ņØĆ Ļ░ÆņØä ļéśĒāĆļé┤ņŚłļŗż. JSC ņ░©ņØ┤ņØś ņøÉņØĖņØä ļČäņäØĒĢśĻĖ░ ņ£äĒĢ┤ external quantum efficiency (EQE, ĻĘĖļ”╝ 2(b))ņÖĆ absorbance (ĻĘĖļ”╝ 2(c)), reflectance (ĻĘĖļ”╝ 2(d)) ļź╝ ņé┤ĒÄ┤ļ│┤ņĢśļŗż. ļ©╝ņĀĆ EQEļź╝ ļ│┤ļ®┤, CuSCN Ļ│╝ NiOx Ļ░Ć ņĀäĒīīņןņŚÉ Ļ▒Ėņ│É ļåÆņØĆ EQEļź╝ ļ│┤ņśĆļŗż. NiOxļŖö ļŗ©ĒīīņןņŚÉņä£ CuSCNļ│┤ļŗż 10% ļé«ņĢśņ¦Ćļ¦ī ņןĒīīņןņŚÉņä£ļŖö ļŹö ļåÆņØĆ EQEļź╝ Ļ░Ćņ¦äļŗż. CuIļŖö ļ╣äĻĄÉņĀü ļåÆņØĆ EQEļź╝ ļéśĒāĆļé┤Ļ│Ā ņ׳ņ£╝ļéś ļŗ©ĒīīņןņŚÉņä£ ļé«ņØĆ Ļ░ÆņØä ļ│┤ņØ┤Ļ│Ā ņ׳ļŗż. Absorbance Ļ▓░Ļ│╝ (ĻĘĖļ”╝ 2(c)) ņÖĆ reflectance (ĻĘĖļ”╝ 2(d))ļź╝ ņ░ĖņĪ░ĒĢ┤ļ│┤ļ®┤, CuIļŖö ļŗ©ĒīīņןņŚÉņä£ NiOxņŚÉ ļ╣äĒĢ┤ ļ╣äĻĄÉņĀü ļåÆņØĆ ļ░śņé¼ņ£©ņØä ļ│┤ņØ┤ļ®░ CuSCNņØĆ ļŗ©ĒīīņןņŚÉņä£ ņāüļīĆņĀüņ£╝ļĪ£ ļé«ņØĆ ĒØĪņłśņ£©ņØä ļ│┤ņØĖļŗż. PEDOT:PSSļŖö ņĀäĒīīņןņŚÉ Ļ▒Ėņ│É ļé«ņØĆ EQEļź╝ ļ│┤ņØ┤ļŖöļŹ░, ĒØĪņłśņÖĆ ļ░śņé¼ ļ¬©ļōĀ ņĖĪļ®┤ņŚÉņä£ ņāüļīĆņĀüņ£╝ļĪ£ ņŚ┤ņ£äļź╝ ļ│┤ņØ┤Ļ│Ā ņ׳ļŗż. Ēæ£ 2ļź╝ ĒÖĢņØĖĒĢ┤ ļ│┤ļ®┤ PEDOT:PSSļŖö ļŗżļźĖ HTL ļ¼╝ņ¦łņŚÉ ļ╣äĒĢ┤ ļé«ņØĆ ļ░┤ļō£Ļ░ŁņØä Ļ░¢Ļ│Ā ņ׳ņØīņØä ņĢī ņłś ņ׳ļŗż. ņØ┤ļĪ£ ņØĖĒĢ┤ ļŗ©ĒīīņןņŚÉņä£ Ļ░Ćņן ļé«ņØĆ ĒØĪņłśņ£©ņØä ļ│┤ņØ╝ ņłśļ░¢ņŚÉ ņŚåļŖöļŹ░ļŗżĻ░Ć, refractive indexĻ░Ć perovskiteņÖĆ Ļ░Ćņן Ēü░ ņ░©ņØ┤ļź╝ ļ│┤ņŚ¼ņŻ╝ĻĖ░ ļĢīļ¼ĖņŚÉ ļ░śņé¼ļÅäļÅä ņ”ØĻ░ĆĒĢśĻ▓ī ļÉśņ¢┤, Ļ│ĀļĀżĒĢ£ ļ¼╝ņ¦ł ņżæ Ļ░Ćņן ļé«ņØĆ ĻĖ░ļīĆĒÜ©ņ£©ņØä ĻĖ░ļĪØĒĢśĻ▓ī ļÉśņŚłļŗż. Ļ│ĀņĀĢļÉ£ ĻĄ¼ņĪ░ļ│ĆņłśņŚÉ ļīĆĒĢ£ Ļ│äņé░ņØä ĒåĄĒĢ┤ Ļ┤æĒĢÖļ¼╝ņä▒ ņĖĪļ®┤ņŚÉņä£ Ļ░Ćņן ĻĖ░ļīĆĒÜ©ņ£©ņØ┤ ļé«ņØĆ ļ¼╝ņ¦łņØĆ PEDOT:PSS ņ×äņØä ļÅäņČ£ĒĢĀ ņłś ņ׳ņŚłļŗż.
3.2. ņĀĢĻ│ĄņłśņåĪņĖĄ ĻĄ¼ņĪ░ņØś ņśüĒ¢ź
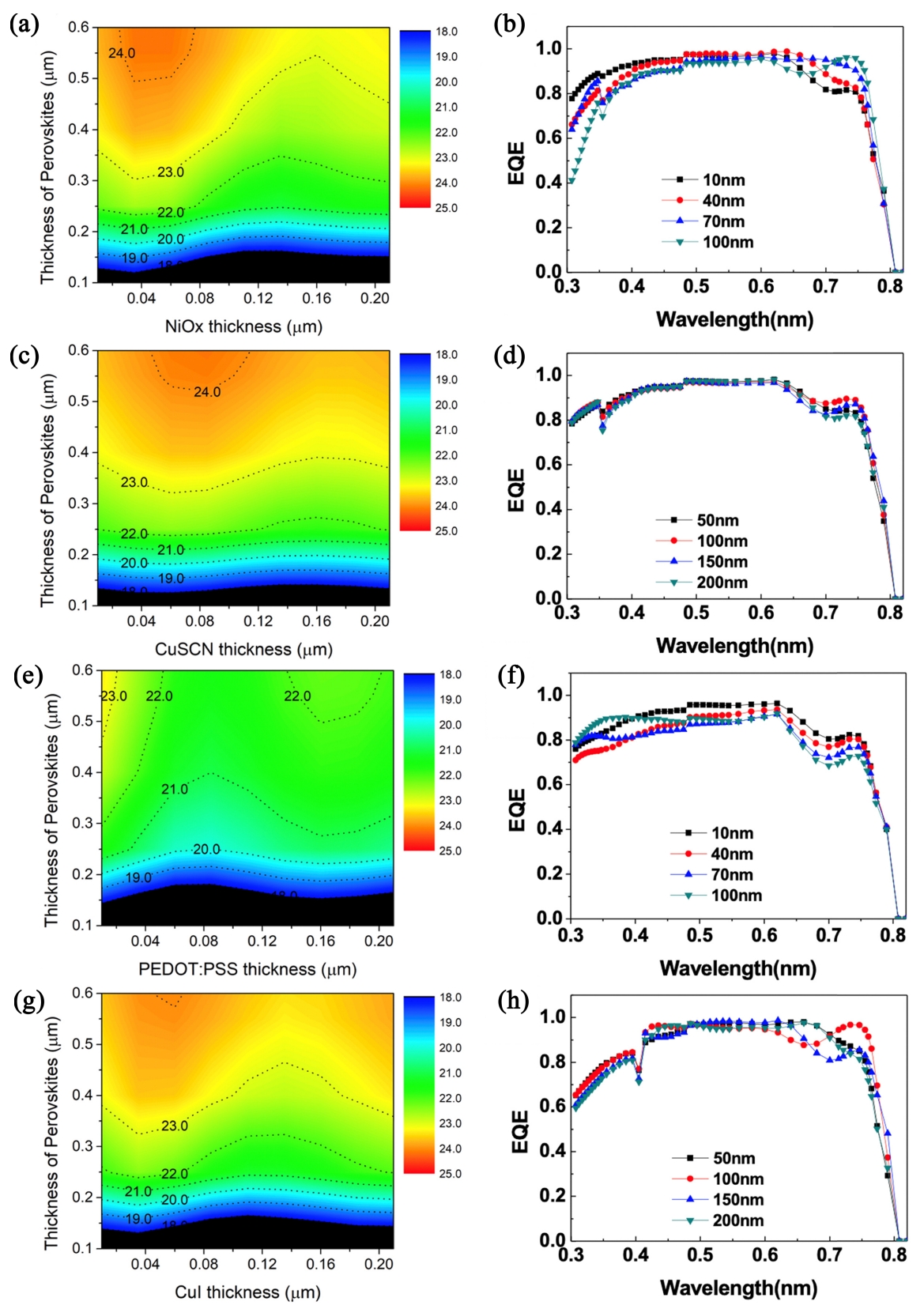
ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖņØś ĻĄ¼ņĪ░ļ│Ćņłśļź╝ Ļ│ĀņĀĢĒĢ£ ņ▒äļĪ£ HTL ļ¼╝ņ¦łņØä ļ│ĆĒÖöņŗ£ņ╝£ Ļ░Ćļ®┤ņä£ ņłśĒ¢ēĒĢ£ Ļ│äņé░ņØä ĒåĄĒĢ┤ PEDOT:PSSļź╝ ņĀ£ņÖĖĒĢ£ ļéśļ©Ėņ¦Ć ļ¼╝ņ¦łļōżņØ┤ ļ╣äĻĄÉņĀü ļÅÖļō▒ĒĢ£ ĒÜ©ņ£©ņØä ļ│┤ņØ╝ ņłś ņ׳ņØīņØä ņĀ£ņŗ£ĒĢĀ ņłś ņ׳ņŚłļŗż. ĻĘĖļĀćņ¦Ćļ¦ī ņØ┤ļ¤¼ĒĢ£ Ļ┤æņĀäļ│ĆĒÖśĒÜ©ņ£©ņØĆ ĻĄ¼ņĪ░ļ│ĆņłśņØś ņśüĒ¢źņØä Ļ│ĀļĀżĒĢ┤ņĢ╝ļ¦ī ĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ, Ļ░ü ļ¼╝ņ¦łļ│äļĪ£ ļæÉĻ╗śņØś ļ│ĆĒÖöĻ░Ć ļ»Ėņ╣śļŖö ņśüĒ¢źņØä ĒÅēĻ░ĆĒĢ┤ņĢ╝ļ¦ī ĒĢ£ļŗż. ņØ┤ļź╝ ņ£äĒĢ┤ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖņØś ļæÉĻ╗śņÖĆ HTL ņØś ļæÉĻ╗śļź╝ Ļ░üĻ░ü 100 nm ~ 600 nm ņÖĆ 20 nm ~ 220 nm ļ▓öņ£äņŚÉņä£ ļ│ĆĒÖöņŗ£ņ╝£Ļ░Ćļ®┤ņä£ ĒÜ©ņ£©ņØś ļ│ĆĒÖöļź╝ Ļ┤Ćņ░░ĒĢśņśĆļŗż (ĻĘĖļ”╝ 3). ņĄ£Ļ│ĀĒÜ©ņ£©ņØś ļÅäņČ£ņØä ņ£äĒĢ┤ ņØ┤ņāüņĀüņØĖ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖņĖĄņØä Ļ░ĆņĀĢĒĢśņśĆĻĖ░ ļĢīļ¼ĖņŚÉ, ļæÉĻ╗śĻ░Ć ņ”ØĻ░ĆĒĢĀ ņłśļĪØ Ļ┤æņĀäļ│ĆĒÖśĒÜ©ņ£©ņØ┤ ņ”ØĻ░ĆĒĢśĻ▓ī ļÉ£ļŗż. ņĢ×ņä£ ņ¢ĖĻĖēĒ¢łļō»ņØ┤, ņØ┤ņāüņĀüņØĖ Ēā£ņ¢æņĀäņ¦Ć ĻĄ¼ņĪ░ņØś Ļ▓ĮņÜ░, ļÅÖņØ╝ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ ļæÉĻ╗ś ņĪ░Ļ▒┤ņŚÉņä£ļŖö JSCĻ░Ć HTL ļ│ĆĒÖöņŚÉ Ļ░Ćņן ļ»╝Ļ░ÉĒĢ£ ņØĖņ×ÉļĪ£ ņ×æļÅÖĒĢśĻ▓ī ļÉ£ļŗż. ņØ┤ņŚÉ ļīĆĒĢ£ ļ╣äĻĄÉ ĒÅēĻ░Ćļź╝ ņ£äĒĢ┤ ļæÉĻ╗śņØś ļ│ĆĒÖöņŚÉ ļö░ļźĖ EQEņØś ļ│ĆĒÖöļź╝ ņäĀļ│äĒĢśņŚ¼ Ļ┤æņĀäļ│ĆĒÖśĒÜ©ņ£©Ļ│╝ ĒĢ©Ļ╗ś ļÅäņŗ£ĒĢśņśĆļŗż (ĻĘĖļ”╝ 3dņØś ņÜ░ņĖĪ ļŗ©). ĻĘĖļ”╝ 3ņŚÉņä£ ņŻ╝ļ¬®ĒĢ┤ņĢ╝ĒĢśļŖö ļČĆļČäņØĆ HTLņØś ļæÉĻ╗śņŚÉ ļö░ļźĖ ĒÜ©ņ£©ļ│ĆĒÖöņØś ņ¢æņāüņØ┤ļŗż. ļŗżļźĖ ļ¼╝ņ¦łņŚÉ ļ╣äĒĢ┤ CuSCNņØä ņé¼ņÜ®Ē¢łņØä ļĢī Ļ░Ćņן ļäōņØĆ ļ▓öņ£äņŚÉ Ļ▒Ėņ│É ņĄ£Ļ│ĀĒÜ©ņ£©ņØś ļÅäņČ£ņØ┤ Ļ░ĆļŖźĒĢ©ņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ņ£╝ļ®░, ņĢ×ņäĀ ļŗ©ņØ╝ ņĪ░Ļ▒┤Ļ│äņé░ņŚÉņä£ ĒÖĢņØĖĒĢ£ Ļ▓āņ▓śļ¤╝, PEDOT:PSSņØś ĻĖ░ļīĆĒÜ©ņ£©ņØ┤ Ļ░Ćņן ļé«Ļ▓ī ļéśĒāĆļé¼ļŗż.
NiOxļŖö 20-80 nmņØś ņ¢ćņØĆ ļæÉĻ╗ś ļ▓öņ£äņÖĆ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖĻ░Ć 500 nm ņØ┤ņāüņØ╝ ļĢī Ļ│ĀĒÜ©ņ£©ņØä ņ¢╗ņØä ņłś ņ׳ļŗż (ĻĘĖļ”╝ 3(a)). ĻĘĖļĀćņ¦Ćļ¦ī NiOxņØś ļæÉĻ╗śņØś ļ│ĆĒÖöņŚÉ ļö░ļØ╝ņä£ ĻĖ░ļīĆĒÜ©ņ£©ņØ┤ ļ¦ÄņØĆ ņśüĒ¢źņØä ļ░øļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. ņØ┤ļŖö EQEņŚÉņä£ļÅä ĒÖĢņØĖĒĢĀ ņłś ņ׳ņŚłļŗż. NiOxņØś ļæÉĻ╗śĻ░Ć ņ”ØĻ░ĆĒĢĀņłśļĪØ ļŗ©Ēīīņן ņśüņŚŁņŚÉņä£ ĻĖēņåŹĒĢśĻ▓ī EQEĻ░Ć Ļ░ÉņåīĒĢśļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż (ĻĘĖļ”╝ 3(b)). NiOxļŖö ļŗ©ĒīīņןņŚÉņä£ ĒØĪņłśĻ│äņłśĻ░Ć ļåÆņĢä ļæÉĻ╗śĻ░Ć ļæÉĻ║╝ņøīņ¦łņłśļĪØ ļŹö ļ¦ÄņØĆ ļ╣øņØä ĒØĪņłśĒĢśņŚ¼ņä£ EQEĻ░Ć Ļ░ÉņåīĒĢśĻ▓ī ļÉ£ļŗż. ļö░ļØ╝ņä£ NiOx ļź╝ HTLļĪ£ ĒÖ£ņÜ®ĒĢĀ Ļ▓ĮņÜ░ ļÉśļÅäļĪØ ņ¢ćĻ│Ā ĻĘĀņØ╝ĒĢ£ ļ░Ģļ¦ēņØä ļ¦īļō£ļŖö Ļ▓āņØ┤ ĒĢäņłśņĀüņØ┤ļØ╝ ĒĢĀ ņłś ņ׳ļŗż. ļ░śļ®┤ņŚÉ CuSCNņØĆ NiOxļ│┤ļŗż ļæÉĻ║╝ņÜ┤ ļæÉĻ╗śņŚÉņä£ļÅä Ļ│ĀĒÜ©ņ£©ņØä ņ¢╗ņØä ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ļ│┤ņØ┤ļ®░ HTL ļæÉĻ╗śņŚÉ ļö░ļźĖ ĒÄĖņ░©ļÅä Ēü¼Ļ▓ī ļéśĒāĆļéśņ¦Ć ņĢŖļŖöļŗż (ĻĘĖļ”╝ 3(c)). CuSCNņØś Ļ▓ĮņÜ░ ĻĄ┤ņĀłļźĀ ņĖĪļ®┤ņŚÉņä£ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖņØś Ļ┤æĒĢÖļ¼╝ņä▒ ņĪ░ĒĢ®ņØ┤ Ļ░Ćņן ņÜ░ņłśĒĢśņŚ¼, ļ░Ģļ¦ē ĻĄ¼ņĪ░ņØś ĒÄĖņ░©ņŚÉļÅä Ļ░Ćņן ņŗĀļó░ļÅä ļåÆņØĆ Ļ▓░Ļ│╝ļź╝ ļ│┤ņŚ¼ņżä ņłś ņ׳ļŖö Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż. EQE Ļ│äņé░Ļ▓░Ļ│╝ (ĻĘĖļ”╝ 3(d)) ļź╝ ļ│┤ļ®┤ CuSCNņØĆ ļŗ©Ēīīņן ņśüņŚŁņŚÉņä£ļÅä ļæÉĻ╗ś ļ│ĆĒÖöņŚÉ ļö░ļØ╝ ņ░©ņØ┤Ļ░Ć Ļ▒░ņØś ļ░£ņāØĒĢśņ¦Ć ņĢŖļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. PEDOT:PSSļŖö ļ░┤ļō£Ļ░ŁņØ┤ 2 eVļĪ£ ļŗżļźĖ ļ¼╝ņ¦łļōżņŚÉ ļ╣äĒĢ┤ ļ¦żņÜ░ ņ×æņĢä ņןĒīīņןņØś ļ╣øņØ┤ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖĻ╣īņ¦Ć ļÅäļŗ¼ĒĢśņ¦Ć ļ¬╗ĒĢ£ļŗż. ļö░ļØ╝ņä£ JSCĻ░Ć ĒśäņĀĆĒ׳ ļé«ņĢäņĀĖ ĒÜ©ņ£©ņŚÉ ņĢģņśüĒ¢źņØä ļ»Ėņ╣£ļŗż. ĻĘĖļ”╝ 3(e) ņŚÉņä£ ĒÖĢņØĖĒĢĀ ņłś ņ׳ļō»ņØ┤ ļæÉĻ║╝ņÜ┤ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ ļ░Ģļ¦ēņŚÉ ņĄ£ņåī ļæÉĻ╗śņØś PEDOT:PSSļź╝ ņé¼ņÜ®ĒĢśļŹöļØ╝ļÅä ĻĖ░ļīĆĒÜ©ņ£©ņØĆ ņāüļīĆņĀüņ£╝ļĪ£ ļé«Ļ▓ī ļéśĒāĆļé£ļŗż. ĻĖ░ļīĆĒÜ©ņ£©ņØś Ēü¼ĻĖ░ļ┐Éļ¦ī ņĢäļŗłļØ╝ ļ░Ģļ¦ē ļæÉĻ╗śņŚÉ ļö░ļźĖ ĒÄĖņ░©ļÅä ņŗ¼ĒĢśĻ▓ī ļéśĒāĆļéśļŖöļŹ░, EQEļź╝ ĒÖĢņØĖĒĢ┤ ļ│┤ļ®┤ ņĀäĒīīņןļīĆņŚÉ Ļ▒Ėņ│É ņāüļīĆņĀüņ£╝ļĪ£ ļé«ņØĆ Ļ░ÆņØä ļ│┤ņØ╝ ļ┐É ņĢäļŗłļØ╝ ļæÉĻ╗śņØś ļ│ĆĒÖöņŚÉ ļīĆĒĢ┤ ļ»╝Ļ░ÉĒĢśĻ▓ī ļ│ĆĒĢśĻ│Ā ņ׳ļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż (ĻĘĖļ”╝ 3(f)). ļ¦łņ¦Ćļ¦ēņ£╝ļĪ£ CuIņØś Ļ▓ĮņÜ░ PEDOT:PSSņŚÉ ļ╣äĒĢ┤ņä£ļŖö ņÜ░ņłśĒĢ£ ĒŖ╣ņä▒ņØä ļ│┤ņØ┤ļéś, NiOx ņÖĆ CuSCNņŚÉ ļ╣äĒĢ┤ņä£ļŖö ņØ┤ņāüņĀü ĒÜ©ņ£©ņØ┤ ļé«ņØĆ Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż (ĻĘĖļ”╝ 3(g)). ņĢ×ņä£ ņ¢ĖĻĖēĒĢ£ Ļ▓āņ▓śļ¤╝ ļŗ©ĒīīņןņŚÉņä£ CuIņØś ļ░śņé¼ļÅäĻ░Ć ļŗżļźĖ ļ¼╝ņ¦łņŚÉ ļ╣äĒĢ┤ ņāüļīĆņĀüņ£╝ļĪ£ ļåÆĻ▓ī ļéśĒāĆļéśĻ▓ī ļÉśļŖöļŹ░, ņØ┤ļĪ£ ņØĖĒĢ┤ EQE Ļ░ÆņØ┤ ļŗ©Ēīīņן ņśüņŚŁļīĆņŚÉņä£ ļé«Ļ▓ī ļéśĒāĆļéśĻ▓ī ļÉśļŖö Ļ▓āņØ┤ ņøÉņØĖņ£╝ļĪ£ ņé¼ļŻīļÉ£ļŗż (ĻĘĖļ”╝ 3(h)).
3.3 ņĀĢĻ│ĄņłśņåĪņĖĄ ļæÉĻ╗śņØś ņśüĒ¢ź
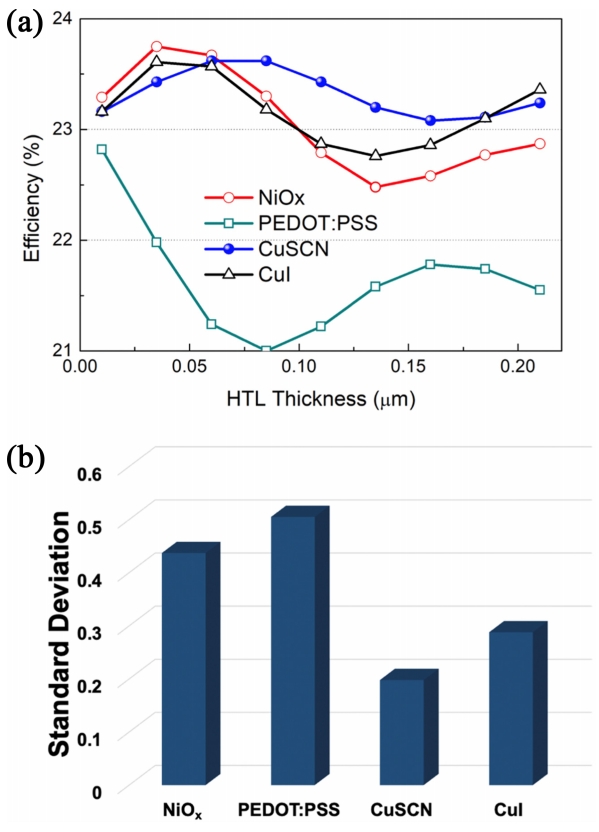
ņ£äņŚÉ ļÅäņŗ£ĒĢ£ Ļ▓░Ļ│╝ņŚÉņä£ ļÅÖņØ╝ĒĢ£ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ ļæÉĻ╗śņŚÉņä£, HTLņØś ĻĄ¼ņĪ░ļ│ĆĒÖöļź╝ ļÅäņŗ£ĒĢśļ®┤ ņĢ×ņä£ ņ¢ĖĻĖēĒĢ£ HTL ļ¼╝ņ¦łņØś ļ│ĆĒÖöĻ░Ć ļ»Ėņ╣śļŖö ņé░ĒżņØś ņśüĒ¢źņØä ņóĆ ļŹö ņēĮĻ▓ī ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. ĻĘĖļ”╝ 4(a)ļŖö ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖņØś ļæÉĻ╗śļź╝ 400 nmļĪ£ Ļ│ĀņĀĢĒĢ£ ņ▒ä, HTLņØś ļæÉĻ╗śņØś ļ│ĆĒÖöĻ░Ć ĒÜ©ņ£©ņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņØä ļÅäņŗ£ĒĢ£ Ļ▓āņØ┤ļŗż. ļæÉĻ╗śņØś ļ│ĆĒÖöņŚÉ ļö░ļØ╝ņä£ Ļ┤æĒØĪņłśņ£©ņØś ļ│ĆĒÖöĻ░Ć ļ░£ņāØĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ ĒŖ╣ņĀĢĒĢ£ ļæÉĻ╗śņŚÉņä£ ņĄ£ņĀüņØś ĒÜ©ņ£©ņØä ļŗ¼ņä▒ĒĢśĻ▓ī ļÉ©ņØä ļ│┤ņŚ¼ņżĆļŗż. PEDOT:PSSļŖö Ļ░Ćņן ĻĖēĻ▓®ĒĢśĻ▓ī ĒÜ©ņ£©ņØś ņĀĆĒĢśĻ░Ć ļ░£ņāØĒĢśļ®┤ņä£ ļæÉĻ╗ś ļ│ĆĒÖöņŚÉ Ļ░Ćņן ļ»╝Ļ░ÉĒĢ£ ļ¼╝ņ¦łņ×äņØä ļ│┤ņŚ¼ņŻ╝ļ®░, NiOx, CuSCN, CuI ļŖö ņĀ£Ļ░üĻ░ü ņĄ£Ļ│Ā ĒÜ©ņ£©ņØä ļŗ¼ņä▒ĒĢĀ ņłś ņ׳ļŖö ļæÉĻ╗śĻ░Ć ļŗżļź┤ļŗżļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. ĻĘĖļ”¼Ļ│Ā ļæÉĻ╗śņŚÉ ļö░ļźĖ ĒÄĖņ░©Ļ░Ć CuSCNņØ┤ Ļ░Ćņן ņĀüņØĆ Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. ņØ┤ļ¤¼ĒĢ£ ĒÄĖņ░©ļź╝ ņĀĢļ¤ēņĀüņ£╝ļĪ£ ĒÖĢņØĖĒĢśĻĖ░ ņ£äĒĢ┤ ņĢ×ņä£ ļÅäņČ£ĒĢ£ Ļ▓░Ļ│╝ņŚÉ ļīĆĒĢ£ Ēæ£ņżĆĒÄĖņ░©ļź╝ ļÅäņČ£ĒĢśņŚ¼ ĻĘĖļ”╝ 4(b)ņŚÉ ļÅäņŗ£ĒĢśņśĆļŗż. ņĀĆļ╣äņÜ® ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ Ēā£ņ¢æņĀäņ¦ĆļŖö ņŻ╝ļĪ£ ņÜ®ņĢĪĻ│ĄņĀĢņØä ĒåĄĒĢ┤ ņĀ£ņĪ░ļÉ£ļŗż. ņØ┤ļ¤┤ Ļ▓ĮņÜ░ Ļ░ü ļ░Ģļ¦ēņĖĄņØś ļæÉĻ╗śļŖö nm ņłśņżĆņ£╝ļĪ£ ĒÅēĒāäĒĢśĻ▓ī ļéśĒāĆļéśĻĖ░ļŖö ļ¦żņÜ░ ņ¢┤ļĀĄļŗż [41]. ņØ┤ļ¤¼ĒĢ£ ļé┤ņ×¼ņĀüņØĖ ļ¼ĖņĀ£ņØś ĻĘ╣ļ│ĄņØä ņ£äĒĢ┤ņä£ļŖö Ēā£ņ¢æņĀäņ¦Ćļź╝ ĻĄ¼ņä▒ĒĢśļŖö ļ░Ģļ¦ēņØś ļæÉĻ╗ś ĒÄĖņ░©ņÖĆ ĒÜ©ņ£©ņØś ņŚ░Ļ┤Ćņä▒ņØ┤ ņĀüņØĆ Ļ▓āņØ┤ ņ£Āļ”¼ĒĢśļŗż. ĒŖ╣Ē׳ļéś ļ¬©ļōłĒÖö ĒĢśņśĆņØä ļĢī Ēā£ņ¢æņĀäņ¦ĆņØś ĒÜ©ņ£©ņØĆ Ļ░Ćņן ļé«ņØĆ Ēā£ņ¢æņĀäņ¦ĆņŚÉ ņØśĒĢ┤ņä£ Ļ▓░ņĀĢļÉśĻĖ░ ļĢīļ¼ĖņŚÉ, ņĄ£Ļ│ĀĒÜ©ņ£©ņØś Ļ░ĆļŖźņä▒ņØ┤ ņ׳ļŖö ļ¼╝ņ¦łņØś ņäĀĒāØļÅä ņżæņÜöĒĢśņ¦Ćļ¦ī ĒÜ©ņ£©ņØś ĒÄĖņ░©ļź╝ ņĄ£ļīĆļĪ£ ņ¢ĄņĀ£ĒĢĀ ņłś ņ׳ļŖö ļ¼╝ņ¦łņØś ņäĀĒāØļÅä ņżæņÜöĒĢśļŗż. ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖņØś ļ░Ģļ¦ē ļæÉĻ╗śņÖĆņØś ņĄ£ņĀü ņĪ░ĒĢ®ņØä ņ░ŠĻ▓ī ļÉśļ®┤ ļŗ¼ņä▒ Ļ░ĆļŖźĒĢ£ ĒÜ©ņ£©ņØĆ 25% ņØ┤ņāüņØ┤ ļÉĀ ņłś ņ׳ļŗżļŖö ĻĘĖļ”╝ 3ņØś Ļ▓░Ļ│╝ļź╝ ļ░öĒāĢņ£╝ļĪ£ ĒĢśņŚ¼, Ļ│ĄņĀĢļ│ĆņłśņØś ļ»╝Ļ░ÉļÅäĻ░Ć Ļ░Ćņן ņĀüņØĆ HTLņØä ņäĀĒāØĒĢ£ļŗżļ®┤ CuSCNņØ┤ Ļ░Ćņן ņ£Āļ”¼ĒĢĀ Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ĒĢĀ ņłś ņ׳ļŗż.
4. Ļ▓░ ļĪĀ
Ļ┤æĒĢÖĻ│äņé░Ļ│╝ ļ░śļÅäņ▓┤ņłśņåĪļ¬©ļŹĖ Ļ│äņé░ņØä ņŚ░Ļ▓░ĒĢ┤ņäØĒĢśļŖö ņłśņ╣śĒĢ┤ņäØ ĻĖ░ļ▓ĢņØä ĒÖ£ņÜ®ĒĢśņŚ¼ inverted type ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ Ēā£ņ¢æņĀäņ¦ĆņØś ņĄ£ņĀü ņĀĢĻ│ĄņłśņåĪņĖĄ ļ¼╝ņ¦łĻ│╝ ĻĄ¼ņĪ░ ĒāÉņāēņØä ņłśĒ¢ēĒĢśņśĆļŗż. NiOx, PEDOT:PSS, CuSCN, CuI ļź╝ ņĀĢĻ│ĄņłśņåĪņĖĄ ļ¼╝ņ¦łļĪ£ ņäĀņĀĢĒĢśņŚ¼ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖņØś ļæÉĻ╗śņÖĆ ņĀĢĻ│ĄņłśņåĪņĖĄņØś ļæÉĻ╗śļ│ĆĒÖöĻ░Ć Ēā£ņ¢æņĀäņ¦ĆņØś ņä▒ļŖźņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņØä ļ╣äĻĄÉ ĒÅēĻ░ĆĒĢśņśĆļŗż. Ļ┤æņĀäļ│ĆĒÖśĒÜ©ņ£©Ļ│╝ HTLņØś ļæÉĻ╗ś ĒÄĖņ░©ņŚÉ ņØśĒĢ£ ņé░Ēżļź╝ ņŻ╝ņÜö ĒÅēĻ░ĆņØĖņ×ÉļĪ£ ĒĢśņŚ¼ Ļ│äņé░Ļ▓░Ļ│╝ļź╝ ļČäņäØĒĢśņśĆļŗż. Ļ│ĀļĀżĒĢ£ ļ¼╝ņ¦ł ņżæ CuSCNņØ┤ ĒÜ©ņ£©Ļ│╝ ņé░Ēż ļæÉ Ļ░Ćņ¦Ć ņĖĪļ®┤ņŚÉņä£ ņÜ░ņłśĒĢ£ ļ¼╝ņ¦łņØ┤ļØ╝ļŖö Ļ▓āņØä ļ░ØĒ×É ņłś ņ׳ņŚłĻ│Ā, CuIņÖĆ NiOxļŖö ĒÜ©ņ£© ņĖĪļ®┤ņŚÉņä£ļŖö CuSCNĻ│╝ ļÅÖļō▒ĒĢśļéś, HTLņĖĄ ļæÉĻ╗śņØś ĒÄĖņ░©ņŚÉ ļö░ļźĖ ĒÜ©ņ£© ļ│ĆĒÖöĻ░Ć ļ╣äĻĄÉņĀü ņŗ¼ĒĢśĻ▓ī ļ░£ņāØĒĢśņŚ¼ ĒÜ©ņ£©Ļ░ÆņØś ņé░Ēż ņĖĪļ®┤ņŚÉņä£ CuSCNņŚÉ ļ╣äĒĢ┤ ļČłļ”¼ĒĢĀ Ļ▓āņ×äņØä ņĀ£ņŗ£ĒĢśņśĆļŗż. PEDOT:PSSļŖö ņāüļīĆņĀüņ£╝ļĪ£ ņóüņØĆ ļ░┤ļō£Ļ░ŁĻ│╝ ļåÆņØĆ ļ░śņé¼ņ£©ļĪ£ ņØĖĒĢ┤ Ļ░Ćņן ļé«ņØĆ ĻĖ░ļīĆĒÜ©ņ£©ņØä ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ņ£╝ļ®░ ņé░ĒżņĖĪļ®┤ņŚÉņä£ļÅä ņÜ░ņłśĒĢśņ¦Ć ļ¬╗ĒĢ£ Ļ▓░Ļ│╝ļź╝ ļ│┤ņśĆļŗż.
PEDOT:PSSļź╝ ņĀ£ņÖĖĒĢ£ ļéśļ©Ėņ¦Ć HTL ļ¼╝ņ¦łņØä ņ░©ņÜ®ĒĢĀ Ļ▓ĮņÜ░, MAPbI3 ļ¼╝ņ¦łņØś ņĄ£ņĀüĒÖöņÖĆ HTL ļ¼╝ņ¦łņØś ļæÉĻ╗ś ņĄ£ņĀüĒÖö Ļ│╝ņĀĢņØä Ļ▒░ņ╣śļ®┤ ĻĖ░ļīĆĒÜ©ņ£©ņØĆ ļ¬©ļæÉ 25% ņØ┤ņāüņØ┤ ļÉĀ Ļ▓āņ£╝ļĪ£ ņśłņĖĪļÉśņŚłļŗż. Ēśäņ×¼ Ļ│ĀĒÜ©ņ£© Ēā£ņ¢æņĀäņ¦ĆņØś ņåīņ×¼ļĪ£ ļ¦ÄņØ┤ ņ▒äĒāØļÉśĻ│Ā ņ׳ļŖö formamidinium lead tri-iodides (FAPbI3) ļ¼╝ņ¦łņØä ņé¼ņÜ®ĒĢĀ Ļ▓ĮņÜ░, ĒØĪņłśĻ░ĆļŖźĒĢ£ ĒīīņןļīĆĻ░Ć ļŹö ļäōņ¢┤ņ¦ĆļŖö ļ¦īĒü╝ Ļ┤æņĀäļ│ĆĒÖśĒÜ©ņ£©ņØĆ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ ņśłņĖĪļÉ£ Ļ░Æļ│┤ļŗż ļŹö ļåÆņØĆ Ļ░ÆņØä ņ¢╗ņØä ņłś ņ׳Ļ▓ī ļÉĀ Ļ▓āņØ┤ļŗż. ļ│Ė ņŚ░ĻĄ¼ļź╝ ĒåĄĒĢ┤ ļÅäņČ£ļÉ£ Ļ▓░Ļ│╝ļź╝ ļ│┤ļ®┤, ņĄ£ņĀüņØś ņåīņ×¼ņÖĆ ņåīņ×ÉĻĄ¼ņĪ░ļŖö ļ¼╝ņ¦łļ│ä Ļ┤æĒĢÖļ¼╝ņä▒Ļ│╝ ņĀäņ×ÉĻĄ¼ņĪ░ņŚÉ ņØśĒĢ┤ ļ¦żļ▓ł ļŗżļź┤Ļ▓ī ļÅäņČ£ļÉśļŖö ļ¦īĒü╝, Ē¢źĒøä ļ│Ė ņŚ░ĻĄ¼ņØś ļ░®ļ▓ĢļĪĀņØä ĒÖĢņן ņĀüņÜ®ĒĢśņŚ¼ ļŗżņ¢æĒĢ£ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ ĻĄ¼ņĪ░ņÖĆ ņĀäĒĢśņłśņåĪņĖĄņäżĻ│äņŚÉ ĒÖ£ņÜ®ĒĢśĻ│Āņ×É ĒĢ£ļŗż.