1. 서 론
열전소재는 형성된 온도 구배를 전기 에너지로 변환하거나 전기 에너지를 온도 구배로 변환할 수 있는 소재로 주목을 받아오고 있다. 열전소재의 성능은 무차원 성능지수인 zT로 주로 표현된다. zT는 zT = S2×σ×T/κtot의 식으로 나타내어진다. 따라서 제벡계수 (S)의 제곱과 전기전도도 (σ)의 곱으로 표현되는 파워팩터 (S2σ)에 비례하고, 전체 열전도도 (κtot)에는 반비례한다 [1]. 열전소재 중에서도, Bi-Te계 합금은 상온에서 전기전도 특성이 높고 열전도도는 낮은 이상적인 물성을 보여 높은 열전 성능을 갖기 때문에 열전 냉각 및 발전에 응용되고 있다 [2,3]. 그러나 Bi-Te계 소재는 기존의 발전 시스템을 대체할 정도의 효율 향상이 이뤄지지 않아 활용이 제한적이다. 특히 zT가 1 이상으로 보고되고 있는 p-type (Bi,Sb)2Te3에 비해 열전성능이 낮은 n-type Bi2(Te,Se)3 합금의 열전 성능 향상을 위한 개발이 필요하다 [4,5].
열전 성능의 향상을 위해 다양한 전략이 시도되어왔으며, 그 중에서도 결함구조를 제어하는 방법이 주로 사용되고 있다. 결함은 크게 외인성 (extrinsic) 결함과 진성 (intrinsic) 결함으로 나눌 수 있다. 외인성 결함을 만드는 치환 도핑은 Bi-Te계 합금 내부에 치환형 점 결함을 형성시켜 격자 열전도도(κlatt)를 낮추고 전기적 물성을 제어하여 zT를 높일 수 있다 [6,7]. p-type (Bi,Sb)2Te3의 양이온 자리에 In 혹은 Cu을 치환 도핑하여, 전기적 특성을 제어함과 동시에 격자 열전도도를 낮추어 zT를 향상시킨 연구가 보고된 바 있다 [8-10].
이와 유사하게, 공공 (vacancy defect), 반자리 결함 (anti-site defect)과 같은 진성결함을 생성시키는 것 또한 zT를 증대시킬 수 있는 전략으로 고려될 수 있다. 진성결함은 Bi-Te계 소재에서 전하 밀도와 포논 산란을 제어해 열전 성능을 향상시킨다 [11,12]. 기존의 n-type Bi2(Te,Se)3에서 Se양을 줄임으로써 공공 결함을 형성해 열전성능을 높인 연구가 보고된 바 있다 [11]. 공공 결함이 형성됨에 따라 전하 밀도가 높아지고, 포논 산란이 더욱 증가하는 효과까지 합쳐져 n-type Bi2(Te,Se)3에서 Se을 0.01 줄인 조성에서 450 K에서 zT가 34% 향상되었다.
본 연구에서는 Cu0.008Bi2Te2.7Se0.3 조성의 n-type 열전소재에서 Te의 화학양론조성을 제어함으로써 (Cu0.008Bi2Te2.7-xSe0.3, x =0, 0.005, 0.01, 0.02) 전하 밀도를 조절하고 전기적 물성을 최적화하였으며, Te 공공에 의한 열전도도의 변화 양상을 분석하여 Cu0.008Bi2Te2.7Se0.3 조성의 열전 특성을 연구하였다. 전기적 전하 수송 특성을 분석하기 위해 Single Parabolic Band (SPB) 모델을 기반으로 한 분석이 진행되었으며, 열전도도 분석을 위해 Debye-Callaway 모델을 적용하였다. Cu 0.008가 첨가된 조성을 적용하여 n-type Bi2(Te,Se)3 조성 소재의 열전 성능의 재현성을 확보하였다 [13].
2. 실험 방법
용융-응고(melt-solidification) 공정을 통해 원료 잉곳을 합성하였다. Shot 형태의 고순도 (99.999%, 5N plus) Bi, Te, Se 및 Cu (Sigma Aldrich, 99.999%)를 Cu0.008Bi2Te2.7-xSe0.3 (x=0, 0.005, 0.01, 0.02)의 조성비에 맞게 칭량한 후 석영관 (직경 15 mm)에 넣었다. 그 다음 진공 (~10-4 torr) 상태가 유지되도록 봉합한 뒤, 1423 K에서 10시간 동안 용융 시켜 잉곳 형태의 원료소재를 제조하였다. 수득된 잉곳은 고에너지 볼 밀(8000M Mixer/Mill, SPEX, Metuchen, NJ, USA)에서 5분간 분쇄되었다. 45 µm의 체로 분말을 걸러낸 뒤, 분말을 773 K, 70 MPa에서 2분동안 Spark Plasma Sintering 방법을 통해 가압소결하였다. 최종적으로 직경 10 mm, 높이 10 mm의 벌크 샘플을 제조했다.
결정상 규명을 위해 X선 회절 (X-ray Diffraction: XRD, Bruker, D8 Discover) 분석을 하였고, 이에 따른 이차상 존재 여부를 확인하였으며 Te deficient 조성에 따른 격자상수의 변화를 산출했다. 범용 측정설비 (ZEM-3, Advanced-Rico, Yokohama, Japan)를 이용하여, 전기전도도와 제벡계수의 온도의존성 분석을 진행하였다. 측정 시, 샘플의 산화를 막기위해 Helium 분위기를 유지했다. 홀 효과 측정 장비 (Hall Effect Measurements System, HMS5500, Ecopia, Anyang, South Korea)를 이용하여 홀 비저항 (Hall resistivity)값을 측정하고, 이로부터 샘플의 전하밀도와 이동도를 계산하였다. 전체 열전도도는 각 측정 샘플의 밀도, 열용량, 열확산계수의 결과값을 이용하여 산출되었다. 샘플의 밀도와 열용량은 이론 값을 이용하였다. 열확산계수는 플래쉬 설비 (Laser Flash Analysis, LFA 467, Netzsch, Erlangen, Germany)를 이용하여 측정되었다. 모든 측정은 가압방향에 수직하도록 샘플을 가공하여 진행하였다.
3. 결과 및 고찰
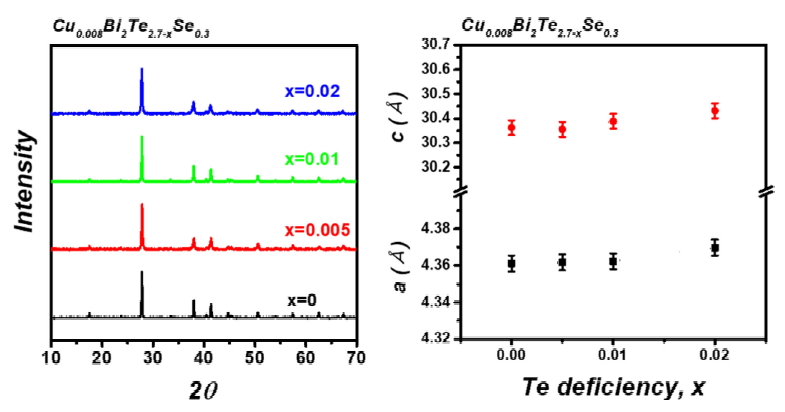
그림 1은 Cu0.008Bi2Te2.7-xSe0.3 (x=0, 0.005, 0.01, 0.02)에 해당되는 샘플들의 소결체 XRD 분석결과이다. 그림 1(a)는 소결체의 XRD 패턴을 나타내며, 이차상이 존재하지 않았기에 Te-deficient를 함에 따라 비화학양론적으로 단일상이 형성되었음을 알 수 있다. 그림 1(b)는 XRD 측정결과로부터 산출한 a축과 c축의 격자상수를 보여주며, Te-deficient에 따른 각 격자상수 변화는 오차범위 정도로 크게 변화하지 않는 것을 확인하였다. Te-deficient 정도가 낮아 Te 공공이 격자상수에 큰 영향을 미치지 않은 것으로 보인다.
그림 2는 전기전도도, 제벡계수와 그에 따른 파워팩터, 전하밀도, 이동도와 같은 샘플의 전기적 특성을 나타내고 있다. Te-deficient에 따라 전기전도도의 증가가 일어나며 (그림 2(a)), 300 K에서 전기전도도는 x=0일 때 962 S/cm에서 x=0.02일 때 1276 S/cm으로 증가하였다. 제벡계수는 전기전도도와 반대로 x=0일 때 -178 µV/K에서 x=0.02일 때 -158 µV/K으로 그 절대값이 감소하였다 (그림 2(b)). 전기전도도와 제벡계수 결과로부터 계산된 파워팩터는 x=0일 때 3.04 mW/mK2에서 x=0.01일 때 3.11 mW/mK2으로 증대되었다 (그림 2(c)).
홀(Hall) 전하밀도와 홀 이동도 결과를 통해 전기적 특성을 더 자세히 규명할 수 있다. 보통 전하밀도와 이동도는 반비례하나, 본 연구에서는 매우 흥미롭게 Te 공공이 증가할 때 홀 이동도는 유지되면서 전하밀도는 증가하는 결과를 확인하였다. 그림 2(d)에 나타낸 바와 같이 전하밀도는 Te deficient 정도에 따라 300 K에서 x=0일 때 2.98×1019 cm-3에서 x=0.02일 때 4.01×1019 cm-3까지 30% 증가하였다. 이는 Te 공공이 생성될 때 전기적 중성을 유지하기 위해 두개의 전자를 동시에 생성하기 때문이다[14]. 한편, 전하 이동도는 최소 199 cm2/Vs (x=0.02) 최대 201 cm2/Vs (x=0)으로 전하밀도의 증가에 비해 거의 일정한 값을 보였다 (그림 2(e)). Te 공공의 형성이 전하의 이동에 영향을 크게 주지 않는 것으로 고려될 수 있다. 그림 2(f)는 300 K에서 제벡계수를 전하밀도에 대해 나타낸 Pisarenko plot이다. 유효질량 (m*)는 페르미 준위에서 전자상태밀도의 유효질량을 나타내며, 이는 전기전도 특성과 큰 관련이 있다. 점선으로 표시된 유효질량은 다음의 (1)식에 의해 계산된 m*=1.0, 1.1, 1.2m0를 나타낸 것이며 m0는 전자의 질량이다.
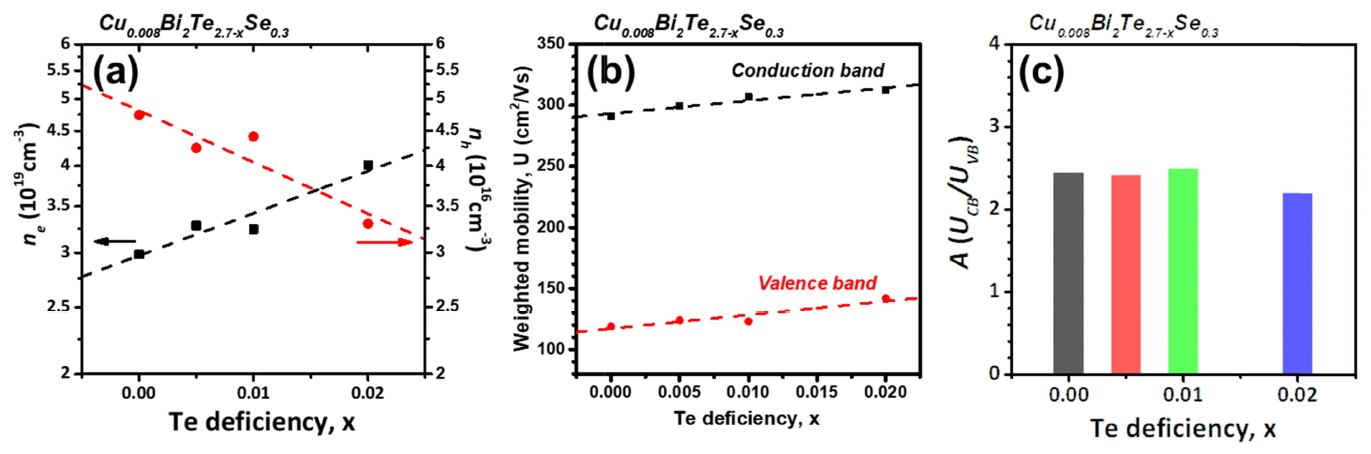
그림 3과 표 1은 전하 수송 물성을 분석하기 위해, Single Parabolic Band (SPB) 모델에서 확장된 two-band 모델을 적용한 결과이다 [15]. 그림 3(a)는 계산된 전자와 정공 밀도를 나타낸다. 전자 밀도의 증가는 기본적으로 홀 전하밀도의 결과와 동일하며, 정공 밀도는 감소하는 것으로 확인되었다. Te 공공에 의한 전자의 형성에 의해 다수 전하인 전자의 밀도는 증가하고, 반대로 공공의 밀도는 감소된 것이다 [14]. 표 1은 SPB 모델에서 도출한 파라미터를 보여주고 있다. 그 중 변형 포텐셜 (Deformation potential, Edef)은 포논에 의한 전하 운반자의 산란 정도를 나타내므로 이동도에 반비례한다. 다수 전하인 전자에 관한 전도대 (Conduction band, CB)의 Edef는 Te-deficient에 따라 그 값이 점점 감소한다. 따라서 Edef 감소로 인한 영향과 이전 그림 2(d)의 홀 전하밀도 증가로 인한 영향이 합쳐져 결과적으로 이동도 값은 거의 일정하게 유지되었다. 그림 3(b)의 가중이동도 (Weighted mobility, U)는 전자상태밀도 유효질량과 비축퇴이동도 (non-degenerate mobility, μ0)의 곱으로 다음과 같이 표현된다. μ0는 (3)식으로 표현된다.
가중이동도는 전하 수송 특성에 관한 것으로, 산출된 UCB가 291 cm2/Vs (x=0)에서 313 cm2/Vs (x=0.02)로 증가하였으며 UVB는 119 cm2/Vs (x=0)에서 142 cm2/Vs (x=0.02)로 증가하였다. 이는 전도대 (CB)의 전자와 가전자대 (Valence band, VB)의 정공 수송 능력이 Te-deficient에 따라 높아짐을 의미한다. 또한, UCB의 값이 313 cm2/Vs으로 가장 큰 x=0.02에서 가장 높은 파워팩터 값을 가진다. 가중이동도의 비율 (UCB/UVB)인 A는 Te-deficient 정도에 따라 그 값이 감소하는 경향을 보여 x=0.02에서 최솟값인 2.21을 가졌다 (그림 3(c)). 이는 양극자 전도 정도가 정공 밀도와 함께 감소할 수 있음을 나타낸다 [16,17].
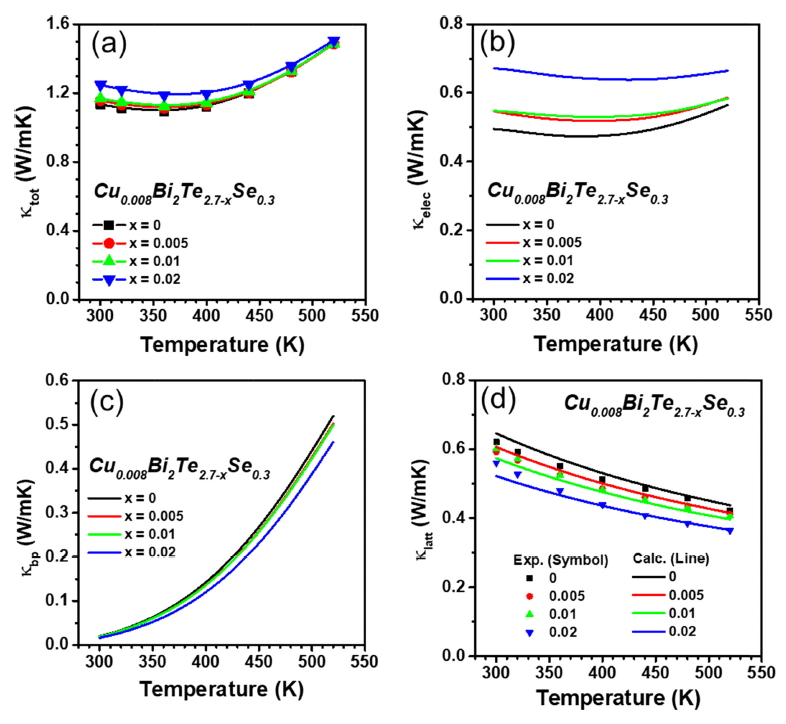
그림 4는 열전도도를 나타내며, 측정된 전체 열전도도 (κtot, 그림 4(a))로부터 전자에 의한 열전도도 (κelec, 그림 4(b)), 양극자에 의한 열전도도 (κbp, 그림 4(c)), 격자에 의한 열전도도 (κlatt, 그림 4(c))를 산출하여 열전도도 변화의 원인을 세 항으로 구분해 규명하고자 하였다. κelec는 (4)식에 해당되는 Wiedemann-Franz law를 이용하여 계산하였다.
κelec은 (4)식으로부터 전기전도도에 비례하므로 Te-deficient에 따라 300 K에서 0.50 W/mK (x=0)으로부터 0.67 W/mK (x=0.02)까지 증가하였다 (그림 4(b)). Bi-Te계 합금은 narrow-gap 반도체이므로 열전도도에 대한 양극성 전도 (Bipolar conduction)의 기여(κbp)가 존재한다 [19]. κbp는 SPB 모델과 Boltzmann transport에 의해 (6)식으로 나타내어 진다.
σp, σn은 각각 가전자대와 전도대의 전기전도도이며, Sp, Sn 또한 각각 가전자대와 전도대의 제벡계수이며, 앞서 SPB 모델을 통해 산출되었다. (6)식으로 산출된 κbp를 그림 4(c)에 나타냈다. Te deficient 정도에 따라 κbp는 점진적으로 줄었다. κbp가 가장 크게 나타나는 520 K에서는, 0.52 W/mK (x=0)에서 0.46 W/mK (x=0.02)으로 줄었다. 이는 Te deficient에 따라 전자 밀도가 증가하고, A가 감소하는 경향을 보이기 때문으로 설명할 수 있다 [19].
그림 4(d)는 κlatt를 나타낸다. 그림 4(d)의 심볼은 실험적으로 구해진 κlatt이고, 이는 측정된 전체 열전도도로부터 κelec과 κbp 값을 빼 산출되었다. 그림 4(d)의 선은 이론적으로 계산한 κlatt이다. 이 값은 반전 산란인자 (Umklapp scattering parameter, U), 점 결함 산란인자 (Point defect scattering parameter, PD), 결정립계 산란인자 (Grain boundary parameter, GB)와 같은 포논 산란에 관한 인자를 계산하는 Debye-Callaway 방적식을 사용해 실험적 κlatt를 피팅해 산출되었다 [20-22]. Te-deficient는 공공을 만드므로, deficient를 함에 따라 추가적으로 점 결함 산란인자를 고려하였다. 점 결함 완화시간은 다음 (7)식에 의해 계산된다.
(7)식에서 P는 피팅 인자이며, f는 substitutional fraction 이다. ω는 포논의 주파수, ν는 포논의 속도, V는 원자 부피이다. Γ는 ΔM (difference in mass), Δa (difference in lattice constant), G (parameter representing a ratio of fractional change of bulk modulus)를 고려한 점 결함 산란 인자이다. 이를 통해 산출된 피팅 인자 P(VTe)와 각각의 조성비(x)를 고려한 값을 표 2에 나타냈다. P(VTe)는 1021×10-41 s3의 값을 보였다. 기존에 알려진 연구에 따르면, Pb 또는 Cu를 치환 도핑하였을 때의 피팅 인자는 각각 PPb=948.7×10-41 s3, PCu=761.8×10-41 s3이다 [23]. P(VTe), PPb, PCu 값 비교를 통해, Te 공공으로 인한 포논 산란효과가 Pb이나 Cu가 치환 도핑됨으로써 생기는 포논 산란효과와 유사하거나 더욱 효율적인 것을 알 수 있다. 한편, P(VTe)에서 조성비를 고려했을 때, 그 값은 x=0.005에서 1.702×10-41 s3, x=0.01에서 3.404×10-41 s3, x=0.02에서 6.808×10-41 s3으로 Te-deficient 정도에 따라 증가하였다. 따라서 그림 4(d)에 선으로 나타낸 이론적 κlatt가 Te deficient에 따라 줄었다.
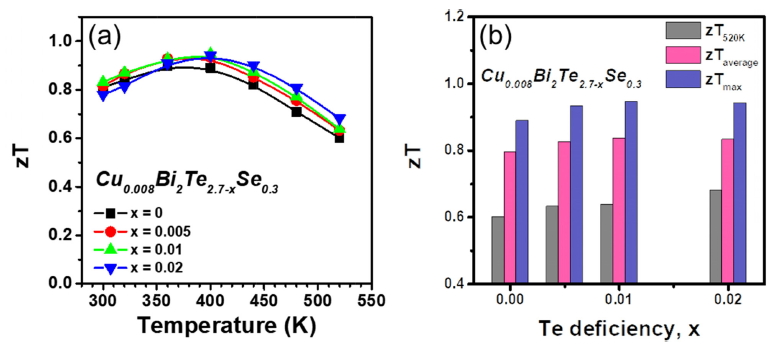
그림 5(a)는 각 조성 (Cu0.008Bi2Te2.7-xSe0.3, x=0, 0.005, 0.01, 0.02)의 파워팩터와 전체 열전도도로 산출한 zT를 온도에 대하여 나타냈다. x=0.005, 0.01 조성의 zT값은 x=0에 비해 300 K-520 K의 전체 온도 범위에서 증가하였고, x=0.02의 조성에서는 360 K부터 zT값이 증가하였다. 이는 Te-deficient 정도에 따른 전기전도도 증가로 인해 파워팩터가 증가함과 동시에, κbp, κlatt의 감소로 인해 κtot의 증가가 비교적 억제되었기 때문이다. 그림 5(b)는 각 조성의 520K에서 zT값 (zT520K), 평균 zT값 (zTaverage), 최대 zT값 (zTmax)을 나타낸다. Te-deficient에 따른 파워팩터의 증가로 인해 zTaverage, zTmax 값은 x=0.01에서 가장 컸다. zTaverage는 x=0의 0.80에서 x=0.01의 0.84로 증가했으며, zTmax는 x=0의 0.89에서 x=0.01의 0.95로 증가했다. 520 K에서의 zT는 고온에서의 zT값이므로 κbp가 크게 관여한다. Te-deficient 정도에 따라 κbp가 감소했으므로 520 K에서 산출된 zT 값은 증가하게 되어, 0.60 (x=0)에서 0.68 (x=0.02)로 증대되었다.
4. 결 론
본 연구를 통해, n-type Cu0.008Bi2Te2.7Se0.3 조성에서 Te-deficient에 따른 전기적 및 열적 특성의 거동변화를 규명하였다. Cu0.008Bi2Te2.7Se0.3에서 Te-deficient 조성 형성을 통해 Te 공공이 생성되었을 때, 전자 수송 능력이 다음과 같이 개선되었다. Te 공공이 생성될 때 전기적으로 중성을 유지하기 위해 전자가 함께 생성되어 전하밀도가 증대되었으며, 이때 전하이동도는 비교적 일정했다. 따라서 전기전도도가 증가하였고 제벡계수는 소폭 감소해, 파워팩터가 3.04 mW/mK2 에서 3.22 mW/mK2 (300 K, x=0.02)로 6% 가량 상승하였다. 전체 열전도도는 Te-deficient 정도에 따라 점차 증가하였으나, Te 공공에 의한 점 결함 포논 산란으로 인한 격자 열전도도 감소가 확인되었다. 결론적으로 파워팩터와 전체 열전도도 모두 증가되었으나, 파워팩터의 증가분의 영향이 상대적으로 커서, x=0.005, 0.01 조성에서는 모든 온도에서 zT가 증대되었다. 평균 zT는 Te 0.01 deficient일 때 약 5% 상승했으며, zT 최댓값은 6% 상승하였으며, 획득한 최대 zT는 Cu0.008Bi2Te2.69Se0.3 (x=0.01) 조성에서 0.95가 얻어졌다.