1. INTRODUCTION
The performance of thermoelectric materials is expressed by the dimensionless figure of merit, ZT = ╬▒2Žā╬║ŌĆō1T, where ╬▒ is the Seebeck coefficient, Žā is the electrical conductivity, ╬║ is the thermal conductivity (╬║ = ╬║E + ╬║L: ╬║E and ╬║L represent the contribution of carriers and phonons to the thermal conductivity, respectively), and T is the absolute temperature [1-3]. To obtain higher ZT values, thermoelectric materials should have a high power factor (PF = ╬▒2Žā) and low thermal conductivity. To achieve higher PF values, the materials must have a large Seebeck coefficient and high electrical conductivity. However, these parameters are interdependent on the carrier concentration. Therefore, it is difficult to control each parameter independently because the thermal conductivity also increases as the electrical conductivity increases [4,5]. In 1994, Slack proposed the phonon-glass and electron-crystal (PGEC) concept, which likens thermal properties to amorphous structures and electrical properties to crystalline structures [6]. Thermoelectric materials conforming to the PGEC concept include the BiŌĆÆTe, PbŌĆÆTe, and SiŌĆÆGe systems, skutterudites, clathrates, etc. Among these materials, skutterudites are attractive because of their high conversion efficiency and concomitant low thermal conductivity and high electrical conductivity [2]. Skutterudites have the basic formula 8MX3 with two large voids in the unit cell. For a filled skutterudite, the thermal conductivity is reduced when the voids are filled with an atom (filler or rattler). Phonon scattering can be enhanced by the rattling effect of these filler atoms with the independent vibrations in the voids. Therefore, the reduced lattice thermal conductivity can result in improved thermoelectric performance [6,7].
Many studies have been conducted to improve the thermoelectric properties of n-type skutterudites. Attempts have been made to achieve higher ZT values of filled n-type skutterudites RyCo4Sb12 (R: filling element and y: filling fraction) by maximizing the power factor through doping [8] and optimizing the fillers [9-11], and by reducing the thermal conductivity through nanostructuring [12,13] and phonon scattering [14,15]. p-Type skutterudites exhibit relatively low ZT values compared to n-type skutterudites [14]. However, thermoelectric devices require both n-type and p-type materials with high stability and excellent performance. Decreasing the lattice thermal conductivity of p-type skutterudites by doping with various atoms and fillers [16-18] has been studied, along with the use of substitutional solid solutions [19]. Double filling in the skutterudite structure is a very effective approach for reducing the lattice thermal conductivity, because each filler atom has a specific resonance frequency and acts as a phonon scattering center [7,20-22]. Among the filler atoms, rare-earth elements with heavier atomic masses can effectively reduce the lattice thermal conductivity by scattering phonons of lower frequencies due to their smaller ionic radii and lower resonance frequencies [7,20,23]. Therefore, double or multiple filling can cause greater phonon scattering, resulting in improved thermoelectric performance [22,24-26].
RyFe4Sb12 is a p-type filled skutterudite that is widely used [23,27,28]. [Co4Sb12] is stable with 72 valence electrons, whereas [Fe4Sb12] is unstable because it has only 68 valence electrons. Therefore, four electrons are required to stabilize the skutterudite phase [27], and the R-filled R4+[Fe4Sb12]4ŌłÆform is possible. However, most elements used as fillers exist in the R2+ and R3+ valence states, leading to a lack of valence electrons [29]. Consequently, charge compensation is required and can be fulfilled by substituting Co or Ni into the Fe site [30]. Recently, some studies have reported that p-type skutterudites cannot be completely filled when the charge is compensated by substituting Co or Ni into the Fe site [31-33]. In addition, completely double-filled and Co-substituted skutterudites produced RSb2 secondary phases because the double filling exceeded the filling fraction limit [34]. In this study, La/Nd-partially-double-filled and Co-substituted p-type (La1ŌłÆzNdz)0.8Fe4ŌłÆxCoxSb12 skutterudites were prepared and their thermoelectric properties were examined.
2. EXPERIMENTAL PROCEDURE
La (purity 99.9%, Kojundo), Nd (purity 99.9%, Kojundo), Fe (purity 99.95%, Cerac), Co (purity 99.95%, Alfa Aesar), and Sb (purity 99.999%, LTS) were weighed according to the stoichiometric compositions of (La1ŌłÆzNdz)0.8Fe4ŌłÆxCoxSb12 (z = 0.25, 0.75 and x = 0, 0.5, 1) and melted in an evacuated quartz tube at 1323 K for 10 h, followed by quenching in water. The resulting ingot was annealed at 873 K for 24 h for phase stabilization and homogenization, and then ground into a powder with a particle size of less than 75 ╬╝m. The synthesized powder was hot-pressed in a graphite die with an internal diameter of 10 mm at 898 K for 1 h under 70 MPa in a vacuum.
The phases of the hot-pressed specimens were analyzed by X-ray diffraction (XRD: Bruker, D8-Advance) with Cu-K╬▒ radiation (40 kV and 30 mA). The diffraction peaks were measured in the ╬ĖŌĆÆ2╬Ė mode with a step size of 0.02┬░, at a scan speed of 0.4 s per step with irradiation at a wavelength of 0.15405 nm. The microstructure was observed by scanning electron microscopy (SEM: FEI, Quanta400), and the chemical composition was analyzed by energy-dispersive spectroscopy (EDS: Bruker, Quantax200). The hot-pressed compacts were cut into rectangular pieces with dimensions of 3 mm ├Ś 3 mm ├Ś 9 mm to measure both the Seebeck coefficient and the electrical conductivity, and also cut into discs with dimensions of 10 mm (diameter) ├Ś 1 mm (thickness) to determine the thermal conductivity. Both the Seebeck coefficient and the electrical conductivity were measured with ZEM-3 (Ulvac-Riko) equipment under He atmosphere. The thermal conductivity (╬║ = Dcpd was evaluated by measuring the thermal diffusivity (D), specific heat (cp), and density (d) under vacuum using the laser flash method with a TC-9000H (Ulvac-Riko) instrument. The power factor and the dimensionless figure of merit were evaluated from the Seebeck coefficient, electrical conductivity, and thermal conductivity.
3. RESULTS AND DISCUSSION
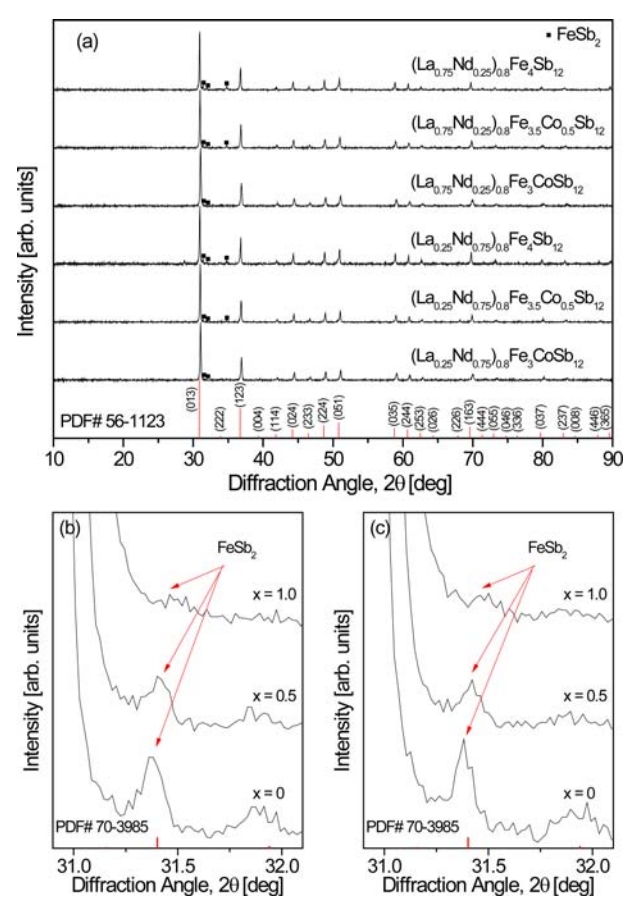
Figure 1 shows the XRD patterns of the (La1ŌłÆzNdz)0.8Fe4ŌłÆxCoxSb12 series. The diffraction peaks of all specimens corresponded to the standard diffraction pattern of the skutterudite phase (ICDD PDF# 56-1123), but a small amount of the marcasite phase FeSb2 (PDF# 70-3985) was detected. However, rareearth antimonides such as LaSb2 and NdSb2 were not produced due to the successful void filling of La and Nd in the skutterudite. The diffraction peaks for marcasite between 31.9┬░ and 32.1┬░ are enlarged in Figs 1(b) and 1(c). Generation of the marcasite phase was suppressed by charge compensation with increasing Co content (x), and thus the intensity of the corresponding diffraction peak decreased. In addition, the diffraction peaks shifted to higher angles with increasing Co content due to the decrease in the lattice constant because the atomic radius of Co (0.167 nm) is smaller than that of Fe (0.172 nm). Therefore, stable skutterudites were successfully synthesized by void filling with La/Nd and Co charge compensation.
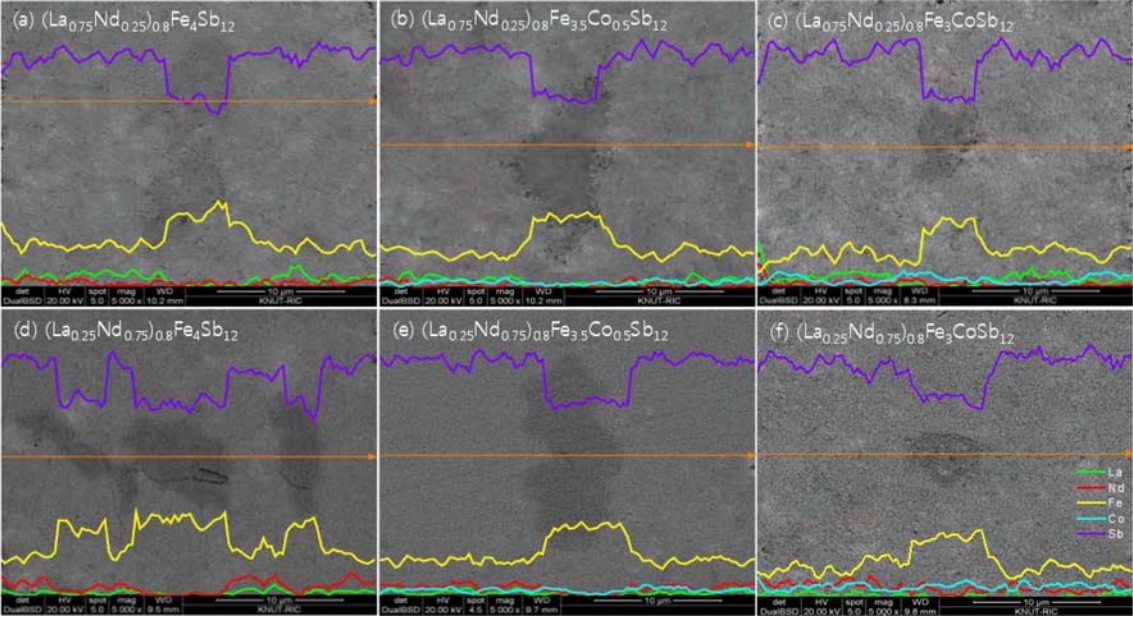
Figure 2 presents the scanning electron microscope (SEM) images and energy dispersive spectroscopy (EDS) line-scans for (La1ŌłÆzNdz)0.8Fe4ŌłÆxCoxSb12. The marcasite phase (dark region) was formed along with the skutterudite phase (bright region). However, as the Co content increased, the signals of the FeSb2 phase became weaker. This is consistent with the XRD analysis. In our previous study [34], (La,Nd)Sb2 phases were observed in the fully-filled La1-zNdzFe4-xCoxSb12 specimens, which was attributed to exceeding the filling fraction limit. However, in the present study, it was confirmed that (La,Nd)Sb2 phases were not formed as the system was only partially filled.
Table 1 shows the chemical compositions, relative densities, and lattice constants of the (La1ŌłÆzNdz)0.8Fe4ŌłÆxCoxSb12 samples. There was no significant change in the actual compositions after hot-pressing relative to the nominal compositions. All specimens had relative densities higher than 98.7% compared with the theoretical density. The calculated lattice constants ranged from 0.9067 to 0.9123 nm depending on the La/Nd filling ratio and the amount of Co used for charge compensation. The lattice constants decreased with increasing Nd and Co content because the ionic radii of Nd (0.127 nm) and Co (0.167 nm) are smaller those of La (0.136 nm) and Fe (0.172 nm) [35-37].
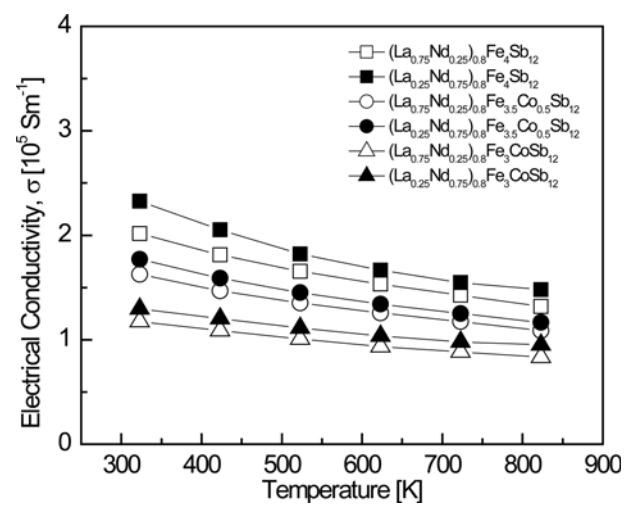
Figure 3 presents the temperature-dependence of the electrical conductivity for (La1ŌłÆzNdz)0.8Fe4ŌłÆxCoxSb12. All specimens behaved like degenerate semiconductors, showing a negative temperature-dependence of the electrical conductivity. The electrical conductivity decreased from (1.17ŌĆÆ2.32) ├Ś 105 S mŌłÆ1 at 323 K to (0.83ŌĆÆ1.47) ├Ś 105 S mŌłÆ1 at 823 K, and decreased with increasing La and Co content in the temperature range of 323 to 823 K. Partially filled (La0.25Nd0.75)0.8Fe4Sb12 showed the highest electrical conductivity of 2.32 ├Ś 105 SmŌłÆ1 at 323 K. The fully-filled La0.25Nd0.75Fe4Sb12 exhibited a maximum electrical conductivity of 2.19 ├Ś 105 SmŌłÆ1 at 323 K [34]. Thus, partial filling increased the electrical conductivity because fewer electrons were donated to the structure than in the case of full filling.
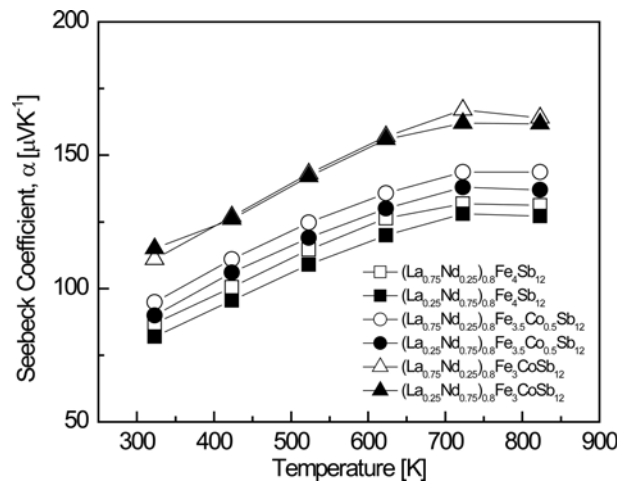
Figure 4 shows the temperature-dependence of the Seebeck coefficient for (La1ŌłÆzNdz)0.8Fe4ŌłÆxCoxSb12. All specimens showed positive values and exhibited p-type characteristics. As the temperature increased, the Seebeck coefficient increased and then decreased at temperatures above a specific temperature. This can be explained by the relationship between the Seebeck coefficient and the carrier concentration. The Seebeck coefficient can be expressed as ╬▒ = (8Ōüä3)ŽĆ2kB2mŌłŚ TeŌĆō1hŌĆō2(ŽĆ Ōüä 3n)2Ōüä3, where kB is the Boltzmann constant, mŌłŚ is the effective hole mass, e is the electronic charge, h is Planck's constant, and n is the carrier concentration. Thus, the Seebeck coefficient increased with increasing temperature, and then decreased because the carrier concentration increased dramatically owing to the intrinsic transition above a specific temperature. In this study, the intrinsic transition temperature of (La1ŌłÆzNdz)0.8Fe4ŌłÆxCoxSb12 was estimated to be 623ŌĆÆ723 K. As the degree of La filling and Co substitution increased, the Seebeck coefficient increased due to the decrease in the carrier concentration. Partially filled Co-doped (La0.75Nd0.25)0.8Fe3CoSb12 showed the highest Seebeck coefficient of 167 ╬╝V KŌłÆ1 at 723 K. All the fully-filled La1ŌłÆzNdzFe4ŌłÆxCoxSb12 samples exhibited the maximum Seebeck coefficient at 823 K, and the highest Seebeck coefficient of 164 ╬╝V KŌłÆ1 at 823 K was achieved with La0.75Nd0.25Fe3.5Co0.5Sb12 [34]. In this study, the partially-filled specimens showed the maximum Seebeck coefficients at 723 K, meaning that the intrinsic transition temperature shifted to lower temperatures due to partial filling.
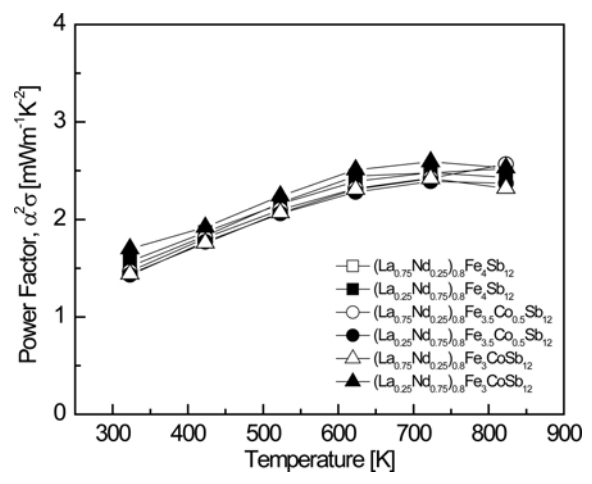
Figure 5 presents the temperature-dependence of the power factor (PF) for (La1ŌłÆzNdz)0.8Fe4ŌłÆxCoxSb12. The PF showed a peak value at a specific temperature owing to the trade-off relationship between the Seebeck coefficient and the electrical conductivity. This is because both parameters depend on the carrier concentration. The PF increased with increasing temperature, and exhibited a maximum value at temperatures between 723 and 823 K. The PF was not significantly influenced by the La/Nd filling ratio or the degree of Co substitution. The PF ranged from 1.43 to 2.59 mW mŌłÆ1 KŌłÆ2 at temperatures from 323 to 823 K, and the highest PF of 2.59 mW mŌłÆ1 KŌłÆ2 at 723 K was obtained with (La0.25Nd0.75)0.8Fe3CoSb12. PF values of 1.49ŌĆÆ2.95 mW mŌłÆ1 KŌłÆ2 were obtained for fully-filled La1ŌłÆzNdzFe4ŌłÆxCoxSb12 at temperatures between 323 and 823 K, and the La0.25Nd0.75Fe4Sb12 composition yielded the highest value of 2.95 m W mŌłÆ1 KŌłÆ2 at 823 K [34]. Therefore, the maximum PF values of the fully and partially filled samples were similar, but the temperature at which the maximum PF appeared was lowered from 823 to 723 K due to partial filling.
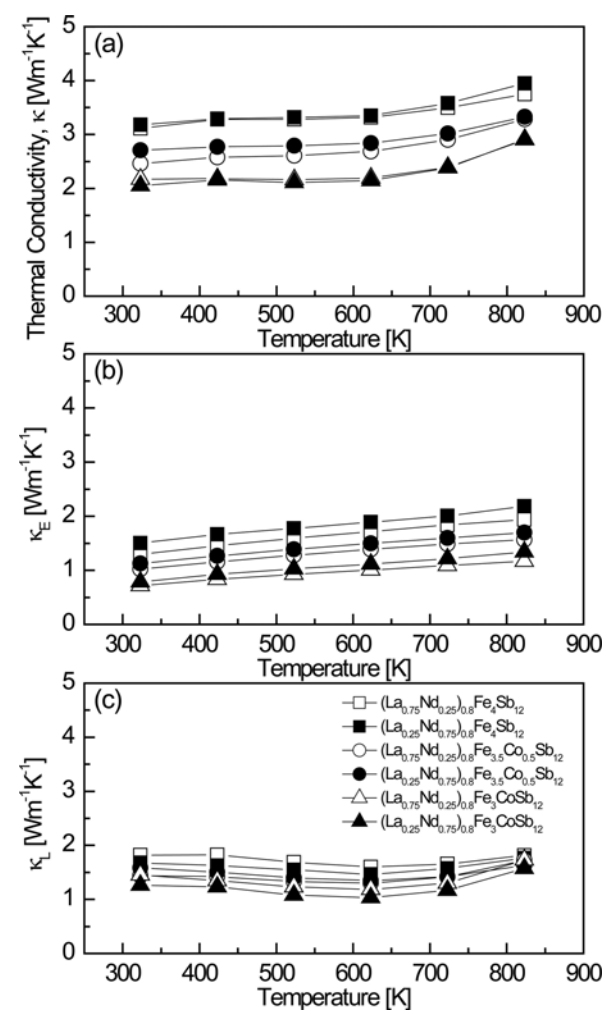
Figure 6 shows the temperature-dependence of the thermal conductivity for (La1ŌłÆzNdz)0.8Fe4ŌłÆxCoxSb12. The change in the thermal conductivity was governed by the degree of Co substitution rather than the La/Nd filling ratio, and as the Co content increased, the thermal conductivity decreased at constant temperature. The thermal conductivity was almost constant with increasing temperature, but increased at temperatures above 623 K due to the bipolar effect. The thermal conductivity ranged from 2.05 to 3.95 W mŌłÆ1 KŌłÆ1 at temperatures between 323 and 823 K. The (La0.25Nd0.75)0.8Fe3CoSb12 sample exhibited the lowest thermal conductivity of 2.05 W mŌłÆ1 KŌłÆ1 at 323 K. The thermal conductivity of the fully-filled La1ŌłÆzNdzFe4ŌłÆxCoxSb12 samples were in the 2.07ŌĆÆ3.01W mŌłÆ1 KŌłÆ1 range at temperatures from 323 to 823 K [34]. The thermal conductivity (╬║) is the sum of the lattice thermal conductivity (╬║L) and the electronic thermal conductivity (╬║E). The ╬║E value can be calculated from the Wiedemann-Franz law (╬║E = LŽāT), where L is the Lorenz number, which was taken as 2.0 ├Ś 10ŌłÆ8 V2 KŌłÆ2 in this study [37].
As shown in Fig 6(b), the electronic thermal conductivity decreased with increasing Co content due to the reduction in the carrier concentration caused by Co charge compensation. The electronic thermal conductivity ranged from 0.71 to 2.18 W mŌłÆ1 KŌłÆ1 at temperatures between 323 and 823 K. (La0.75Nd0.25)0.8Fe3CoSb12 showed the lowest electronic thermal conductivity of 0.71W mŌłÆ1 KŌłÆ1 at 323 K. The electronic thermal conductivity was lowest (1.10 W mŌłÆ1 KŌłÆ1 at 323 K) for fully-filled La0.75Nd0.25Fe3.5Co0.5Sb12 [34]. As shown in Fig 6(c), the lattice thermal conductivity was lowest for all specimens (1.03ŌĆÆ1.59 W mŌłÆ1 KŌłÆ1) at 623 K. With increasing Co substitution, the lattice thermal conductivity decreased due to enhanced phonon scattering by the impurity. However, the La/Nd filling ratio had no significant impact on the lattice thermal conductivity. (La0.25Nd0.75)0.8Fe3CoSb12 showed the lowest lattice thermal conductivity of 1.03W mŌłÆ1 KŌłÆ1 at 623 K. Fully-filled La1ŌłÆzNdzFe4ŌłÆxCoxSb12 showed the minimum lattice thermal conductivity at temperatures between 623 and 723 K, and La0.25Nd0.75Fe3.75Co0.25Sb12 showed the lowest value of 0.68 W mŌłÆ1 KŌłÆ1 at 623 K [34]. Thus, partial filling slightly increased the lattice thermal conductivity. Filled skutterudites have been reported to be effective for enhancing phonon scattering as a result of low-resonance frequency scattering due to heavy filler elements or small ionic radii of the filler elements [22-26,35]. It was expected that the use of La and Nd, which are heavy and have small ionic radii, as the filler elements would reduce the lattice thermal conductivity by improving the phonon scattering. However, the enhancement of the phonon scattering was insignificant due to the similar atomic masses and ionic radii of La and Nd. As a result, the partially-filled specimens showed higher lattice thermal conductivities than the fully-filled specimens. However, the electronic thermal conductivity decreased with Co charge compensation; thus, the total thermal conductivities of the partially- and fully-filled specimens were similar.
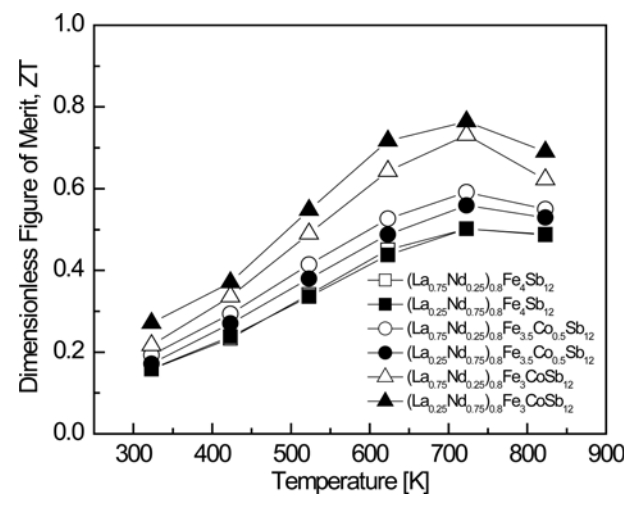
Figure 7 presents the temperature-dependence of the dimensionless figure of merit (ZT) for (La1ŌłÆzNdz)0.8Fe4ŌłÆxCoxSb12. The ZT values increased with increasing temperature, and all specimens exhibited a maximum ZT value at 723 K. (La0.25Nd0.75)0.8Fe3CoSb12 showed the highest ZT value of 0.76 at 723 K. However, for the fully-filled La0.75Nd0.25Fe4Sb12, ZTmax = 0.82 at 823 K, and for La0.25Nd0.75Fe3.75Co0.25Sb12, ZTmax = 0.78 at 723 K [34]. The ZT values of the partiallyfilled specimens were slightly lower than those of the fullyfilled specimens. In this study, we expected to suppress the formation of secondary phases by partial double filling with La and Nd, and to optimize the carrier concentration by Co charge compensation. In addition, we aimed to enhance the phonon scattering in order to improve the thermoelectric performance by reducing the lattice thermal conductivity. However, the improvement in the phonon scattering derived from partial double filling was insignificant due to the similar ionic radii and atomic masses of La and Nd. Compared with the fully-filled specimens, the lattice thermal conductivity of the partially filled specimens was relatively high; thus, the thermoelectric performance could not be enhanced effectively. Park et al. [38] reported ZTmax = 0.56 at 823 K for LaFe4Sb12 and Shin et al. [39] obtained ZTmax = 0.78 at 823 K for NdFe4Sb12. Joo et al. [40] reported ZTmax = 0.74 at 723 K for La0.5Yb0.5Fe3CoSb12 and Shin et al. [41] attained ZTmax = 0.84 at 823 K for (Pr0.75Nd0.25)0.8Fe3CoSb12. Compared with these other studies, the maximum ZT was achieved at lower temperatures in this study, and thus these species are expected to be applicable for thermoelectric power generation in the mid-temperature range.
4. CONCLUSIONS
Partially double-filled p-type (La1ŌłÆzNdz)0.8Fe4ŌłÆxCoxSb12 skutterudites were synthesized by capsulated melting and subsequent sintering by hot pressing. All specimens were transformed into the skutterudite phase by annealing, but a small amount of the marcasite phase was also formed. (La,Nd)2 phases were not produced because the filling fraction limit was not exceeded by partial filling. The formation of marcasite was inhibited by Co charge compensation. The Seebeck coefficients were positive, indicating that all specimens had p-type characteristics. As the degree of Nd filling and Co substitution increased, the Seebeck coefficient increased and the electrical conductivity decreased due to the decreased carrier concentration. The maximum Seebeck coefficient of the partially filled specimens was achieved at lower temperature than the fully-filled specimens. Consequently, the maximum power factor was obtained at temperatures between 723 and 823 K, and the highest power factor of 2.59 mW mŌłÆ1 KŌłÆ2 at 723 K was obtained with the (La0.25Nd0.75)0.8Fe3CoSb12 composition. No significant improvement in the phonon scattering was derived from partial double filling due to the similar ionic radii and atomic masses of La and Nd. Therefore, the lattice thermal conductivity can be reduced further. (La0.25Nd0.75)0.8Fe3CoSb12 exhibited a maximum dimensionless figure of merit, ZTmax, of 0.76 at 723 K.