1. INTRODUCTION
Higher manganese silicide (HMS) is a promising thermoelectric material for thermoelectric generations at intermediate temperatures, as it is eco-friendly, non-toxic, and has abundant constituents [1]. The HMS has several phases with a Nowotny chimney-ladder (NCL) structure, including Mn11Si19 (MnSi1.72), Mn15Si26 (MnSi1.73), Mn27Si47 (MnSi1.74), and Mn4Si7 (MnSi1.75) [2–4]. This NCL structure belonging to the tetragonal system is composed of a ladder-shaped sub-lattice of Mn and helical-chimney-shaped sub-lattice of Si. Among the doping elements of HMS, V, Cr, and Mo substitute Mn sites, while Al and Ge are doped at Si sites. Among these dopants, Ge is reported as one of the most effective ways to control the transport properties of HMS [1,5,6]. Ge doping improves the power factor (PF) by increasing the charge carrier concentration and induces point defects by changing the electronic structure, thereby reducing the lattice thermal conductivity through enhanced phonon scatterings [7–10]. Lee et al. [1] reported a high dimensionless figure of merit (ZT) of 0.64 at 773 K for MnSi1.75:Ge0.028 prepared by solid-state reaction (SSR) and spark plasma sintering (SPS).
However, the thermal conductivity can be increased owing to the secondary phases (MnSi and Si) and self-defects (Si vacancies), usually generated in the synthesis of the doped HMS [9]. In order to achieve high ZT values, secondary phases and self-defects should be suppressed. The distribution of the plate-like MnSi was confirmed when molten HMS was solidified during quenching [10]. Therefore, in order to inhibit the formation of the MnSi phase, solid-state synthesis processes have been employed, such as mechanical alloying (MA) [11,12] and SSR [1,10,13]. In our previous studies [14,15], the formation of secondary phases could be suppressed by SSR; Al- and Cr-doped HMSs were successfully synthesized by SSR. In this study, Ge-doped HMS powders (MnSi1.72:Gem and MnSi1.73:Gem) were synthesized by SSR and consolidated by hot pressing (HP), and their thermoelectric properties were studied.
2. EXPERIMENTAL METHODS
Elemental powders of Mn (purity: 99.9%), Si (purity: 99.99%), and Ge (purity: 99.99%) were weighed to the desired stoichiometries of MnSi1.72:Gem and MnSi1.73:Gem (m = 0.01-0.04), followed by ball milling for 30 min to achieve uniform mixtures. The mixed powder was then placed into an alumina crucible and subjected to SSR at 1273 K for 6 h in vacuum. The synthesized powder was crushed to fine powder with particle sizes smaller than 75 μm and then charged into a graphite mold with an inner diameter of 10 mm and subjected to HP at 1173 K for 2 h under 70 MPa.
An X-ray diffraction (XRD, Bruker D8-Advance) analysis was performed using Cu-Kα radiation (40 kV, 30 mA, λ = 0.15405 nm) in the θ-2θ mode at a scan step of 0.02° and scan speed of 3°/min. XRD patterns were obtained from powders synthesized by SSR and sintered bodies formed by HP. The lattice constants were calculated by the Rietveld refinement method (Bruker, TOPAS). Elemental mapping was performed to observe the microstructures of the sintered specimens and verify the distributions of constituent elements in the specimens using a scanning electron microscope (SEM, FEI Quanta400) equipped with an energy-dispersive spectrometer (EDS, Bruker, Quantax200).
Thermoelectric properties were measured and analyzed in the temperature range of 323 K to 823 K. The Seebeck coefficient (α) and electrical conductivity (σ) were measured by the temperature differential and DC four-probe method (Ulvac-Riko, ZEM-3) in a He atmosphere:
where kB is the Boltzmann constant, e is the electron charge, h is the Planck constant, m* is the effective carrier mass, T is the absolute temperature, n is the carrier concentration, and μ is the mobility. The thermal conductivity (κ) was evaluated using Eq. 3 by measuring the thermal diffusivity (D), specific heat (cp), and density (d) by the laser flash method (Ulvac-Riko, TC-9000H):
3. RESULTS AND DISCUSSION
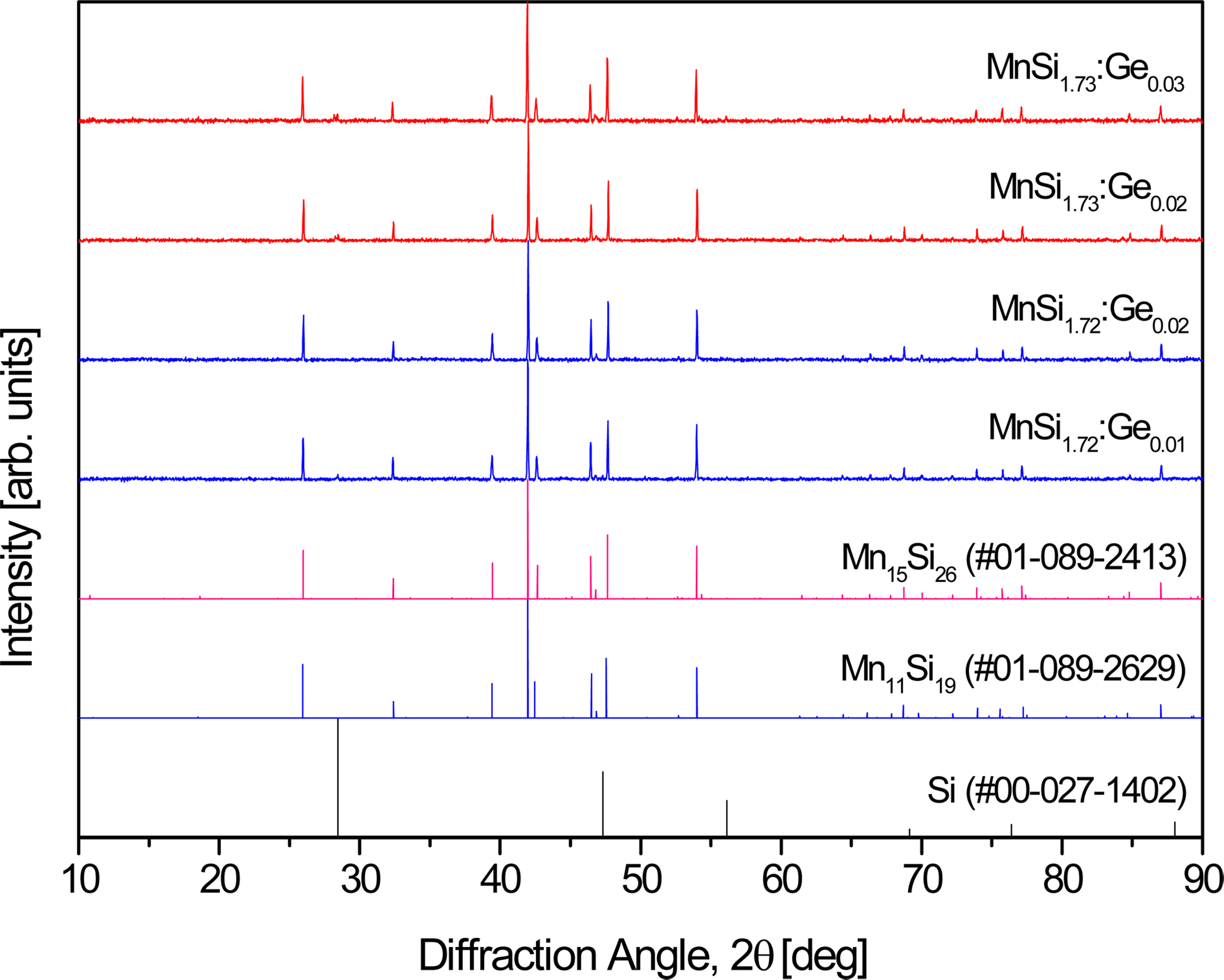
Figure 1 shows the XRD patterns of MnSi1.72:Gem and MnSi1.73:Gem powders synthesized by SSR. All the diffraction peaks of MnSi1.72:Gem and MnSi1.73:Gem were well matched with standard data of Mn11Si19 (PDF #01-089-2629) and Mn15Si26 (PDF #01-089-2413), respectively. Therefore, Ge-doped HMS phases were successfully synthesized. MnSi was not observed in this study, but a small amount of Si remained, possibly due to the substitution of Ge for Si and Si vacancies as self-defects [9].
Figure 2 presents the XRD patterns of the MnSi1.72:Gem and MnSi1.73:Gem specimens sintered by HP. Phase transformations were not observed after the HP. The diffraction peaks shifted to lower angles with the increase in the Ge substitution concentration. For example, as shown in Figs. 2(b) and 2(c), the diffraction peaks corresponding to the planes (21-11) and (2115) shifted to lower angles with the increase in the Ge content, which implies that the HMS lattice with the NCL structure was expanded by the Ge substitution. The calculated lattice constants of MnSi1.72:Gem and MnSi1.73:Gem are shown in Table 1. The lattice constants increased with the Ge content owing to the difference in covalent radius between Ge (0.122 nm) and Si (0.117 nm) [6]; the increase along the c-axis was larger than that along the a-axis. Therefore, the SSR-HP processes are suitable to fabricate the Ge-doped HMSs, as reconfirmed in this study.
Fig. 2.
(a) XRD patterns of MnSi1.72:Gem and MnS1.73Gem specimens sintered using HP, and (b) and (c) enlarged XRD peaks showing the peak shifts due to Ge doping.
Table 1.
Lattice constants of MnS1.72:Gem and MnSiu1.73Gem
Figure 3 shows SEM images and EDS elemental mappings of the HP specimens. Fractured surfaces of MnSi1.72:Ge0.01 and MnSi1.73:Ge0.03 are illustrated as typical examples. The specimens had dense and compact sintered bodies, where the Mn, Si, and Ge elements were homogeneously distributed.
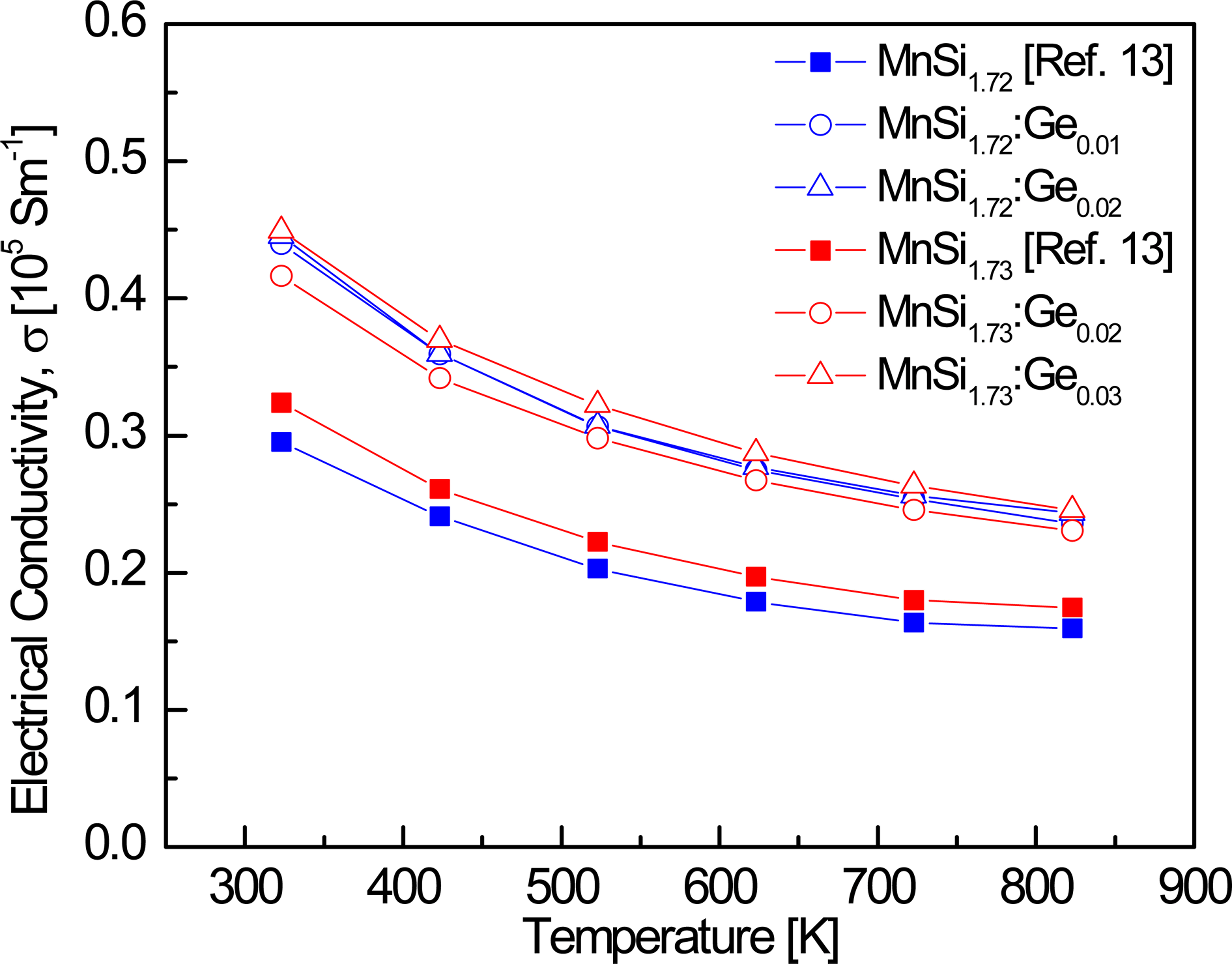
Figure 4 presents the temperature dependence of the electrical conductivities of MnSi1.72:Gem and MnSi1.73:Gem. The electrical conductivity decreased with the increase in the temperature, i.e., a negative temperature dependence was observed, corresponding to a metallic or degenerate-semiconductor behavior. At all analyzed temperatures, Ge doping significantly enhanced the electrical conductivities of MnSi1.72 and MnSi1.73, which increased with the Ge content. Al acts as a p-type dopant in the HMS system owing to its smaller valence than that of Si, providing additional holes by substituting Al for Si; therefore, the electrical conductivity of HMS can be increased by Al doping [16]. However, although Ge and Si have equal valences, the electrical conductivity is increased by the Ge doping. This is attributed to the changes in the Si-Si bonding affected by the Ge substitution; consequently, the Si lattice distorted by the Ge substitution helps the charge carriers (holes) enhance the electrical conductivity [7–10]. MnSi1.73:Ge0.03 exhibited the highest electrical conductivities of 4.5 × 104 Sm−1 at 323 K and 2.5 × 104 Sm−1 at 823 K.
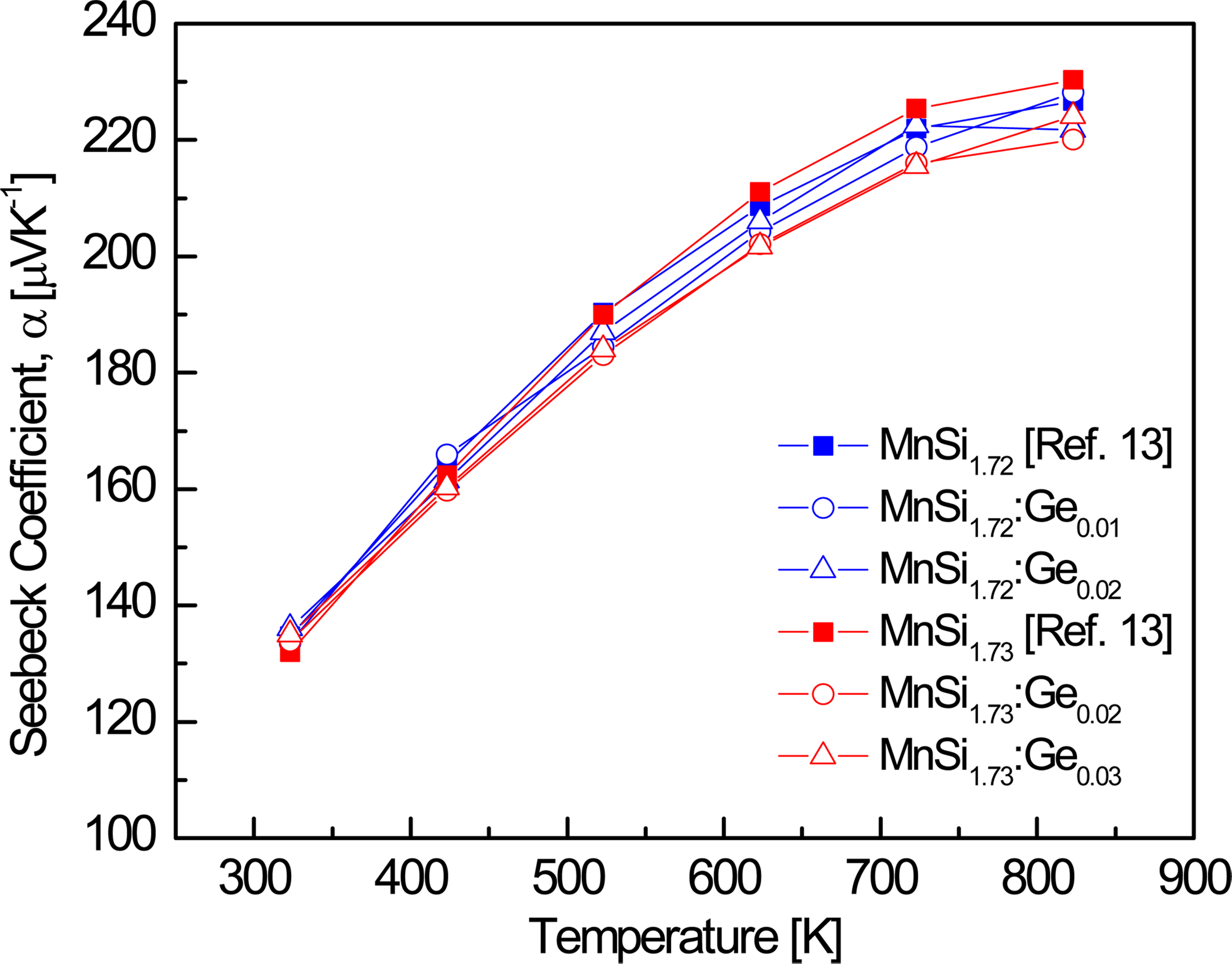
Figure 5 shows the temperature dependence of the Seebeck coefficients of MnSi1.72:Gem and MnSi1.73:Gem. The Seebeck coefficients had positive values in the whole measured temperature range, which implies that major charge carriers were holes (p-type conduction). The Ge-doped HMSs had slightly lower Seebeck coefficient values than the undoped MnSi1.72 and MnSi1.73. As shown in Eqs. 1 and 2, the Seebeck coefficient was also affected by the carrier concentration and mobility (i.e., effective mass). Therefore, the Ge doping increased the electrical conductivity and decreased the Seebeck coefficient. The Seebeck coefficient increased with the temperature; the temperature dependence weakened at high temperatures as the Seebeck coefficient was proportional to the temperature but inversely proportional to the carrier concentration. The significant increase in the carrier concentration, attributed to intrinsic transitions at high temperatures, decreased the Seebeck coefficient, 228 μVK−1 for MnSi1.72:Ge0.01 and 224 μVK−1 for MnSi1.73:Ge0.03 at 823 K.
Figure 6 presents the temperature dependence of the PFs of MnSi1.72:Gem and MnSi1.73:Gem. The PF increased with the temperature with peak values at certain temperatures owing to the “trade-off” relationship between the electrical conductivity and Seebeck coefficient, as shown in Eq. 4. This was attributed to the degenerate-semiconductor behavior of the electrical conductivity and effect of intrinsic transitions on the Seebeck coefficient. The PF was remarkably increased by the Ge doping owing to the significant increase in the electrical conductivity and slight decrease in the Seebeck coefficient. Maximum PF values were obtained at 823 K, 1.26 mWm−1K−2 for MnSi1.72:Ge0.02 and 1.23 mWm−1K−2 for MnSi1.73:Ge0.03.
Figure 7 shows the temperature dependence of the thermal conductivities of MnSi1.72:Gem and MnSi1.73:Gem. The thermal conductivity (κ) is a sum of the electronic thermal conductivity (κe), lattice thermal conductivity (κ1), and bipolar thermal conductivity (κbi), attributed to the effects of carrier concentration, phonon scattering, and bipolar conduction, respectively. The difference in atomic mass (Si: 28.08, Ge: 72.59) can lead to phonon scattering; therefore, the lattice thermal conductivity can be decreased by the Ge substitution. In the case of MnSi1.72:Gem, the Ge substitution was not very effective to the thermal conductivity. However, the thermal conductivity of MnSi1.73:Gem increased with the Ge doping as the increase in the electronic thermal conductivity owing to the increased carrier concentration was larger than the decrease in the lattice thermal conductivity owing to the enhanced phonon scattering. The total thermal conductivity decreased with the increase in the temperature with minimum values at temperatures between 623 K and 723 K owing to bipolar conduction. The lowest thermal conductivity of κ = 2.07 Wm−1K−1 was achieved at 623 K for MnSi1.72:Ge0.01.
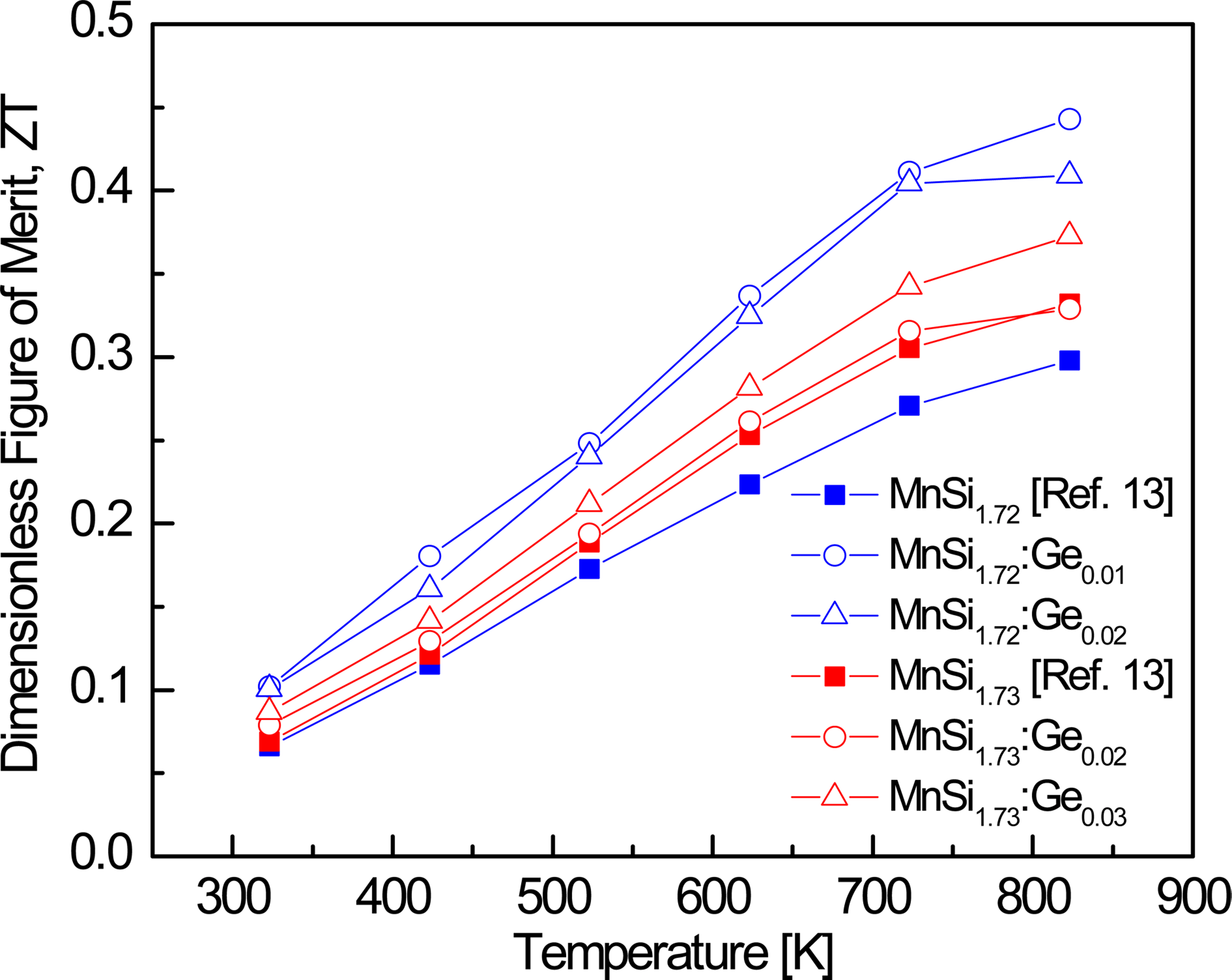
Figure 8 presents the ZT values of MnSi1.72:Gem and MnSi1.73:Gem. In our previous studies, the maximum ZT values of undoped MnSi1.72 and MnSi1.73 were 0.29 [13] and 0.33 [13] at 823 K, respectively, while the maximum ZT values of doped MnSi1.73:Al0.005 and MnSi1.73:Cr0.01 were 0.41 [14] and 0.36 [15] at 823 K, respectively. In this study, the PF was enhanced with the increase in the temperature, while the thermal conductivity maintained low values at high temperatures; therefore, the ZT values were significantly increased with the temperature. In addition, the enhanced PF by the Ge doping could further improve the ZT values. In the MnSi1.72:Gem systems, MnSi1.72:Ge0.01 exhibited the maximum ZT of 0.44 at 823 K, while in the MnSi1.73:Gem systems, MnSi1.73:Ge0.03 exhibited the maximum ZT of 0.37 at 823 K.
4. CONCLUSION
Ge-doped HMSs (MnSi1.72:Gem and MnSi1.73:Gem) were prepared by SSR and HP, and their thermoelectric properties were evaluated. The XRD analysis showed that Ge was successfully substituted for Si. The MnSi phase was not identified. The electrical conductivity and PF increased with the Ge content owing to the increased charge carrier concentration. However, the Ge doping slightly decreased the Seebeck coefficient. In the case of MnSi1.73:Gem, the Ge substitution increased the thermal conductivity, while in the case of MnSi1.72:Gem, it did not significantly affect the thermal conductivity. The Ge doping improved the ZT, yielding values of 0.44 for MnSi1.72:Ge0.01 and 0.37 for MnSi1.73:Ge0.03 at 823 K.