1. ņä£ ļĪĀ
ņ▓ĀĻ░Ģņ×¼ļŻīļŖö ĻĘ╝ļīĆ ņé░ņŚģņé¼ĒÜīņŚÉņä£ Ļ░Ćņן ļäÉļ”¼ ņé¼ņÜ®ļÉ£ ĻĄ¼ņĪ░ņ×¼ļŻīļĪ£, ļŗżņ¢æĒĢ£ ĒĢ®ĻĖł ņä▒ļČäņØä Ļ░Ćņ¦Ćļ®░, ļÅÖņŗ£ņŚÉ ļ»ĖņäĖņĪ░ņ¦üņØä ņĀüņĀłĒ׳ ņĪ░ņĀłĒĢśņŚ¼ ļ¦żņÜ░ ļŗżņ¢æĒĢ£ ņĀ£ĒÆł Ēś╣ņØĆ ņé░ņŚģņŚÉ ņé¼ņÜ®ļÉśĻ│Ā ņ׳ļŗż. ĻĘĖ ņżæ Ļ░Ćņן ļäÉļ”¼ ņé¼ņÜ®ļÉśĻ│Ā ņ׳ļŖö ņ▓ĀĻ░Ģņ×¼ļŻīļŖö ņĀĆĒāäņåīĻ░Ģņ£╝ļĪ£, ņāüņś©ņŚÉņä£ ņŻ╝ļĪ£ ĒÄśļØ╝ņØ┤ĒŖĖ(ferrite) ņĪ░ņ¦üņØä Ļ░¢ļÅäļĪØ Ļ│ĄņĀĢ ņĪ░Ļ▒┤ņØ┤ ņäżņĀĢļÉ£ļŗż. ĒŖ╣Ē׳ ņ×ÉļÅÖņ░© ņé░ņŚģĻ│╝ Ļ░ÖņØĆ Ļ│ĀļČĆĻ░ĆĻ░Ćņ╣ś ņé░ņŚģņØ┤ ĻĖēņåŹļÅäļĪ£ ļ░£ņĀäĒĢśĻ│Ā ļÅÖņŗ£ņŚÉ ņ╣£ĒÖśĻ▓Į ņé░ņŚģ ļČäņĢ╝ņŚÉ ĒāäņåīĻ░ĢņØä ņĀüņÜ®ĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņÜ░ņłśĒĢ£ Ļ░ĢļÅäņÖĆ ņŚ░ņä▒ņØ┤ ņÜöĻĄ¼ļÉśĻ│Ā ņ׳ļŗż. ņØĖņä▒ņØś Ļ░Éņåī ņŚåņØ┤ Ļ░ĢļÅäļź╝ ļåÆņØ╝ ņłś ņ׳ļŖö ĻĖ░ĻĄ¼ļĪ£, Hall-Petch Ļ┤ĆĻ│äņŚÉ ļö░ļźĖ Ļ▓░ņĀĢļ”Į ļ»ĖņäĖĒÖö ĻĖ░ĻĄ¼Ļ░Ć ņĄ£ĻĘ╝ 20ļģäĻ░ä ļäÉļ”¼ ņĀüņÜ®ļÉśņ¢┤ ņÖöļŗż. ņāüņś©ņŚÉņä£ ĒÄśļØ╝ņØ┤ĒŖĖĻ░Ć ļ»ĖņäĖļ”ĮņØä Ļ░¢ĻĖ░ ņ£äĒĢ┤ņä£ļŖö Ļ│Āņś©ņŚÉņä£ ņĢłņĀĢĒĢ£ ņśżņŖżĒģīļéśņØ┤ĒŖĖ(austenite)ļź╝ ņÜ░ņäĀņĀüņ£╝ļĪ£ ļ»ĖņäĖĒÖö ņŗ£ņ╝£ņĢ╝ ĒĢ£ļŗż. ņŚ┤ņŚ░ Ļ│ĄņĀĢņŚÉņä£ ņśżņŖżĒģīļéśņØ┤ĒŖĖļź╝ ļ»ĖņäĖĒÖöņŗ£ĒéżĻĖ░ ņ£äĒĢ£ ļ░®ļ▓Ģ ņżæ ĒĢśļéśļĪ£ ņĀĢņĀü Ēś╣ņØĆ ļÅÖņĀü ņ×¼Ļ▓░ņĀĢ(static or dynamic recrystallization of austenite) ĒśäņāüņØ┤ ņ׳ļŗż. C. M. Sellars, T. Sakai, J. Jonas [1,2]ļŖö ņśżņŖżĒģīļéśņØ┤ĒŖĖņØś ļÅÖņĀü ņ×¼Ļ▓░ņĀĢņŚÉ Ļ┤ĆĒĢ£ ņŚ░ĻĄ¼ļź╝ ļŗżņ¢æĒĢ£ ļ¬©ņé¼ ņŗżĒŚśņØä ĒåĄĒĢ┤ ņłśņ╣śĒÖöņŗ£ĒéżĻ│Āņ×É ļģĖļĀźĒĢśņśĆļŗż. ņØ┤ļ¤¼ĒĢ£ ņłśņ╣śĒÖö ņ×æņŚģņØĆ ņĢ×ņä£ ļ®┤ņŗ¼ ņ×ģļ░® ĻĄ¼ņĪ░ļź╝ Ļ░¢ļŖö ņ×¼ļŻīņŚÉņä£ ņåīņä▒ ņŚŁĒĢÖņØä ļ░£ņĀäņŗ£ņ╝£ ņś© H. MeckingĻ│╝ U. F. Kocks [3,4] ņÖĆ Y. EstrinĻ│╝ H. Mecking [5] ĻĘĖļ”¼Ļ│Ā H. MeckingĻ│╝ B. Nicklas, N. Zarubova [6]ņØś ņŚ░ĻĄ¼ Ļ▓░Ļ│╝ļź╝ ļ░öĒāĢņ£╝ļĪ£ ņłśĒ¢ēļÉśņŚłļŗż. ĒŖ╣Ē׳ Ļ│Āņś©ņŚÉņä£ ņĢĢņČĢ, ņØĖņן, ļ╣äĒŗĆļ”╝ ļ¬©ņé¼ ņŗżĒŚśņØä ĒåĄĒĢ┤ņä£ ņ£ĀļÅÖ ņØæļĀź Ļ│ĪņäĀņØś ĒĢ┤ņäØņØä ļ»ĖņäĖņĪ░ņ¦üĻ│╝ ņŚ░Ļ┤Ćņŗ£ņ╝£ ņŚ░ĻĄ¼ĒĢ©ņ£╝ļĪ£ņŹ©, Ļ│Āņś©ņŚÉņä£ņØś ņ£ĀļÅÖ ņØæļĀź Ļ│ĪņäĀņØä ĒåĄĒĢ┤ ļ»ĖņäĖņĪ░ņ¦üņØä ņśłņĖĪĒĢĀ ņłś ņ׳ļŖö ĻĖ░ļ░śņØä ļ¦łļĀ©ĒĢśņśĆļŗż [1-6]. ĻĄŁļé┤ņŚÉņä£ļÅä ņ▓ĀĻ░Ģņ×¼ļŻīņØś ļÅÖņĀü ņ×¼Ļ▓░ņĀĢ ĒśäņāüņŚÉ ļīĆĒĢ£ ņ£ĀļÅÖ ņØæļĀź Ļ│ĪņäĀ ĒĢ┤ņäØ Ēś╣ņØĆ ņ£ĀĒĢ£ ņÜöņåīļ▓Ģ ļō▒ņØä ņĀüņÜ®ĒĢ£ ļ¦ÄņØĆ ņŚ░ĻĄ¼Ļ░Ć ņ¦äĒ¢ēļÉśņŚłļŗż [7,8]. ļśÉĒĢ£ ņ▓ĀĻ░Ģ ņ×¼ļŻīļ┐Éļ¦ī ņĢäļŗłļØ╝ ņĀäĒåĄņĀüņØĖ ĻĖłņåŹņ×¼ļŻī ņżæ ĒĢśļéśņØĖ ņĢīļŻ©ļ»ĖļŖä ĒĢ®ĻĖł [9], ĒāĆņØ┤ĒāĆļŖä ĒĢ®ĻĖł [10-12] ļō▒ņŚÉļÅä ļÅÖņØ╝ĒĢ£ ņ£ĀļÅÖ ņØæļĀź Ļ│ĪņäĀ ļ¬©ņé¼ ņŗżĒŚśņØ┤ ņĀüņÜ®ļÉśņŚłņ£╝ļ®░, ņĄ£ĻĘ╝ņŚÉļŖö Ļ│Ā ņŚöĒŖĖļĪ£Ēö╝ ĒĢ®ĻĖł(high entropy alloy)[13,14]ņŚÉļÅä ņĀüņÜ®ļÉśļŖö ņé¼ļĪĆĻ░Ć ļ│┤Ļ│ĀļÉśĻ│Ā ņ׳ļŗż.
YadaņÖĆ ĻĘĖņØś ļÅÖļŻīļōżņØĆ ņśżņŖżĒģīļéśņØ┤ĒŖĖņØś ļÅÖņĀü ņ×¼Ļ▓░ņĀĢņØ┤ ņØ╝ņ¢┤ļéśļŖö ņś©ļÅä ĻĄ¼Ļ░äņŚÉņä£ ņśżņŖżĒģīļéśņØ┤ĒŖĖņŚÉ Ļ░ĢĒĢ£ ņåīņä▒ ļ│ĆĒśĢņØä Ļ░ĆĒĢśļŖö Ļ│╝ņĀĢņŚÉ ņśżņŖżĒģīļéśņØ┤ĒŖĖņØś ļÅÖņĀü ņ×¼Ļ▓░ņĀĢ ļ┐Éļ¦ī ņĢäļŗłļØ╝ ĒÄśļØ╝ņØ┤ĒŖĖļĪ£ņØś ņāüļ│ĆĒā£Ļ░Ć ļ░£ņāØĒĢśļŖö ļÅÖņĀü ņāüļ│ĆĒā£(dynamic transformation)ļź╝ ņ▓śņØī ļ│┤Ļ│ĀĒĢśņśĆļŗż [15,16]. ņØ┤Ēøä ļ¦ÄņØĆ ņŚ░ĻĄ¼ņ×ÉļōżņØ┤ ņåīņä▒ ļ│ĆĒśĢ ņżæņŚÉ ļ░£ņāØĒĢśļŖö ņāüļ│ĆĒā£ņŚÉ ļīĆĒĢ┤ņä£ ņŚ░ĻĄ¼ļź╝ ņ¦äĒ¢ēĒĢśņśĆņ£╝ļ®░, ļ╣äĻĄÉņĀü ļŗ©ņł£ĒĢ£ Ļ│ĄņĀĢņØä ĒåĄĒĢ┤ ņ┤łļ»ĖņäĖļ”ĮņØä Ļ░¢ļŖö ņ▓ĀĻ░Ģņ×¼ļŻīļź╝ Ļ░£ļ░£Ē¢łļŗżļŖö ļ│┤Ļ│ĀĻ░Ć ņĄ£ĻĘ╝ ļ░£Ēæ£ļÉśĻ│Ā ņ׳ļŗż [15-21]. ĒŖ╣Ē׳ Zhao ļō▒ņØĆ ļÅÖņĀü ņāüļ│ĆĒā£ļź╝ ņØ╝ņ£╝ņ╝£ ĒÄśļØ╝ņØ┤ĒŖĖņØś Ļ▓░ņĀĢļ”ĮņØä ļ»ĖņäĖĒÖö ņŗ£ĒéżļŖö Ļ▓āņŚÉ ĻĘĖņ╣śņ¦Ć ņĢŖĻ│Ā, ĒÄśļØ╝ņØ┤ĒŖĖņØś ļÅÖņĀü ņ×¼Ļ▓░ņĀĢ ĒśäņāüņØä ņĢ╝ĻĖ░ņŗ£ĒéżļŖö ņĪ░Ļ▒┤ņØä ņ░ŠņĢśņ£╝ļ®░, ĻĖ░ņĪ┤ņŚÉ Ļ░Ģņåīņä▒ņ£╝ļĪ£ļ¦ī ļ¦īļōż ņłś ņ׳ņŚłļŹś ņ┤łļ»ĖņäĖļ”ĮņØä ņĀüņØĆ ļ│ĆĒśĢļ¤ēņ£╝ļĪ£ ņ¢╗ņØä ņłś ņ׳ņŚłļŗż. ņØ┤ļź╝ ļ░öĒāĢņ£╝ļĪ£ ĒĢŁļ│ĄĻ░ĢļÅäĻ░Ć 800 MPaņŚÉ ņ£Īļ░ĢĒĢśļ®░ ņŚ░ņŗĀņ£©ņØ┤ 20%ļź╝ ņ┤łĻ│╝ĒĢśļŖö ļ¦żņÜ░ ĒøīļźŁĒĢ£ ĻĖ░Ļ│äņĀü ĒŖ╣ņä▒ņØä ņ¢╗ņØä ņłś ņ׳ļŖö ņĀĆĒāäņåī(0.1 wt%) ņ▓ĀĻ░Ģ ĒĢ®ĻĖł ļ░Å Ļ│ĄņĀĢņØä Ļ░£ļ░£ĒĢśņśĆļŗż.
ņØ┤ļ¤¼ĒĢ£ ļÅÖņĀü ņāüļ│ĆĒā£ ĒśäņāüņØ┤ ĻĖ░ņĪ┤ņØś ņĀĢņĀü ņāüļ│ĆĒā£Ļ░Ć ļ░£ņāØĒĢśļŖö ņś©ļÅä ĻĄ¼Ļ░ä ņØ┤ņāüņŚÉņä£ ļ░£ņāØĒĢ£ļŗżļŖö ļ│┤Ļ│ĀĻ░Ć ņØ╝ļČĆ ņ׳ņŚłņ£╝ļ®░, Gibbs ņ×Éņ£Ā ņŚÉļäłņ¦Ć Ļ│äņé░ ļō▒ņØä ĒåĄĒĢ┤ Ļ░ĆļŖźņä▒ņØ┤ ņØ╝ļČĆ ņĀ£ĻĖ░ļÉśņŚłļŗż. ĒĢśņ¦Ćļ¦ī ļ»ĖņäĖĻĄ¼ņĪ░ Ļ┤Ćņ░░ ņŗżĒŚśņØä ĒåĄĒĢ┤ ļ░ØĒśĆļé┤ĻĖ░ņŚÉ ņŗżĒŚśņĀüņØĖ ņśżļźśĻ░Ć Ēü¼Ļ▓ī ļ░£ņāØĒĢśņŚ¼ ņŗĀļó░ĒĢĀ ņłś ņŚåņŚłļŹś ļ¼ĖņĀ£Ļ░Ć ņ׳ņŚłļŗż. Park ļō▒ņØĆ ņĢ×ņä£ ņ£ĀļÅÖ ņØæļĀź Ļ│ĪņäĀņØä ļŗżņ¢æĒĢ£ ņĪ░Ļ▒┤ņŚÉņä£ ņ¢╗ņØĆ Ēøä, Ļ░ĆĻ│Ą ņś©ļÅä ļ░Å ļ│ĆĒśĢņ£© ņåŹļÅäņØś Ļ┤ĆĻ│äļź╝ Ļ░¢ļŖö Zener-Hollmon Ļ┤ĆĻ│äņŗØņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņāłļĪ£ņÜ┤ ņŗ£ļÅäļź╝ ĒĢśņśĆļŗż [18,19,22]. ņØ┤ļź╝ ĒåĄĒĢ┤, ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć ļ╣Āļź╝ņłśļĪØ Ae3 ņś©ļÅäļ│┤ļŗż ļåÆņØĆ ņś©ļÅäņŚÉņä£ļÅä ļÅÖņĀü ņāüļ│ĆĒā£Ļ░Ć ņØ╝ņ¢┤ļéĀ ņłś ņ׳ņØīņØä ļŗżņØīĻ│╝ Ļ░ÖņØĆ Ļ│╝ņĀĢņØä ĒåĄĒĢ┤ ļ░ØĒśĆļāłļŗż. ņÜ░ņäĀ Ļ│Āņś©ņŚÉņä£ ņśżņŖżĒģīļéśņØ┤ĒŖĖļŖö ņåīņä▒ ļ│ĆĒśĢņŚÉ ļö░ļØ╝ Ļ▓ĮĒÖö(strain hardening) ļ░Å ļÅÖņĀü ĒÜīļ│Ą(dynamic recovery, DRV)ņØ┤ ņØ╝ņ¢┤ļé£ļŗż. Ļ│Āņś©ņŚÉņä£ ņĀäņ£äņØś cross-slipņŚÉ ņØśĒĢ£ ņŚ░ĒÖö(softening) ĒśäņāüĻ│╝ ņ×¼Ļ▓░ņĀĢ ĒĢĄņāØņä▒ņØä ĒåĄĒĢ┤ ļÅÖņĀü ņ×¼Ļ▓░ņĀĢ ĒśäņāüņØ┤ ļéśĒāĆļéśļ®┤ņä£ ņŚ░ĒÖöļÉśļ®░ ņ£ĀļÅÖ ņØæļĀź ņ”ØĻ░Ć ņåŹļÅäĻ░Ć Ļ░ÉņåīĒĢśĻ▓ī ļÉ£ļŗż. ņØ┤Ēøä, ņĄ£ļīĆ ņ£ĀļÅÖ ņØæļĀźņØä Ļ░Ćņ¦ä Ēøä, ĻĖēĻ▓®Ē׳ ļÅÖņĀü ņ×¼Ļ▓░ņĀĢ ļČäņ£©ņØś ņ”ØĻ░ĆļĪ£ ņØĖĒĢ┤ ņ£ĀļÅÖ ņØæļĀźĻ░ÆņØ┤ Ļ░ÉņåīĒĢśļŖö ĒśäņāüņØä ļ│┤ņØĖļŗż. Parkļō▒ņØĆ ņØ┤ļ¤¼ĒĢ£ ĒśäņāüņØ┤ ļ╣äļŗ© ņśżņŖżĒģīļéśņØ┤ĒŖĖņØś ļÅÖņĀü ņ×¼Ļ▓░ņĀĢņŚÉļ¦ī ņØ╝ņ¢┤ļéśļŖö ĒśäņāüņØ┤ ņĢäļŗī, ļÅÖņĀü ņāüļ│ĆĒā£ņŚÉņä£ļÅä ļéśĒāĆļéśļŖö Ļ▓āņØä ļ░£Ļ▓¼ĒĢśņśĆļŗż. ņä£ļĪ£ ļŗżļźĖ ļæÉ ĒśäņāüņØä Ļ┤Ćņ░░ĒĢśļ®░ ņĄ£ļīĆ ņ£ĀļÅÖ ņØæļĀźĻ░ÆļōżņØś ņ░©ņØ┤ļź╝ ņ¢╗ņŚłņ£╝ļ®░, ņØ┤ļź╝ ļŗżņ¢æĒĢ£ ņś©ļÅäņÖĆ ļ│ĆĒśĢņ£© ņåŹļÅä ļ│ĆĒÖöļź╝ ĒåĄĒĢ®ĒĢśņŚ¼ ņäżļ¬ģĒĢĀ ņłś ņ׳ļŖö Zener-Hollmon Ļ┤ĆĻ│äņŗØņØä ĒÖ£ņÜ®ĒĢśņŚ¼ ļÅÖņĀü ņāüļ│ĆĒā£Ļ░Ć ņØ╝ņ¢┤ļéśļŖö ĒŖ╣ņĀĢĒĢ£ ņĪ░Ļ▒┤ņØä ļ░£Ļ▓¼ĒĢśņśĆļŗż [18]. ĒĢśņ¦Ćļ¦ī ņ£ĀļÅÖ ņØæļĀź Ļ│ĪņäĀņØś ņĄ£ļīĆ ņØæļĀźĻ░ÆņØä ĒÖ£ņÜ®ĒĢ£ļŗżļŖö Ļ▓āņØĆ ņØ┤ļ»Ė ņĢĮ ņłś% ņØ┤ņāüņØś ĒÄśļØ╝ņØ┤ĒŖĖļĪ£ņØś ļÅÖņĀü ņāüļ│ĆĒā£ Ēś╣ņØĆ 15% ņłśņżĆņØś ņśżņŖżĒģīļéśņØ┤ĒŖĖņØś ļÅÖņĀü ņ×¼Ļ▓░ņĀĢņØ┤ ļ░£ņāØļÉ£ ļŗżņØīņŚÉ ļéśĒāĆļéśļŖö Ļ░ÆņØ┤ĻĖ░ ļĢīļ¼ĖņŚÉ, ļÅÖņĀü ņāüļ│ĆĒā£ ĒśäņāüņØä ļ»╝Ļ░ÉĒĢśĻ▓ī Ļ┤Ćņ░░ĒĢĀ ņłś ņŚåļŗżļŖö ĒĢ£Ļ│äņĀÉņØ┤ ņĀ£ĻĖ░ļÉśņŚłļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņåīņä▒ ļ│ĆĒśĢņŚÉ ļö░ļźĖ Ļ▓ĮĒÖöņÖĆ ļÅÖņĀü ĒÜīļ│ĄņØ┤ ļÅÖņŗ£ņŚÉ ņØ╝ņ¢┤ļéśļŖö ĻĄ¼Ļ░ä, ņ”ē ņĄ£ļīĆ ņ£ĀļÅÖ ņØæļĀźņŚÉ ļÅäļŗ¼ĒĢśĻĖ░ ņĀä ņāüĒā£ņØś ņ£ĀļÅÖ ņØæļĀź Ļ│ĪņäĀņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņāłļĪ£ņÜ┤ ĒĢ┤ņäØņØä ņŗ£ļÅäĒĢśņŚ¼, ņśżņŖżĒģīļéśņØ┤ĒŖĖņØś ļÅÖņĀü ņ×¼Ļ▓░ņĀĢņ£╝ļĪ£ļČĆĒä░ ĒÄśļØ╝ņØ┤ĒŖĖļĪ£ņØś ļÅÖņĀü ņāüļ│ĆĒā£ļź╝ ņśłņĖĪĒĢśĻ│Āņ×É ĒĢ£ļŗż.
2. ņŗżĒŚś ļ░®ļ▓Ģ
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö 0.1 wt% ĒāäņåīņÖĆ 6 wt% ļŗłņ╝łņØä Ļ░¢ļŖö ĒĢ®ĻĖłņ▓ĀņØä ņØ┤ņÜ®ĒĢśņśĆļŗż. ļŗłņ╝łņØä ņ▓©Ļ░ĆĒĢ£ ļ¬©ļŹĖ ĒĢ®ĻĖłņ£╝ļĪ£, ņśżņŖżĒģīļéśņØ┤ĒŖĖ ņśüņŚŁņØä ņóĆļŹö ļé«ņØĆ ņś©ļÅäļĪ£ ĒÖĢņןņŗ£ņ╝£ ĒÄśļØ╝ņØ┤ĒŖĖ ņāüļ│ĆĒā£ļź╝ ņ¦ĆņŚ░ņŗ£ĒéżĻ│Āņ×É ņäżĻ│äĒĢśņśĆļŗż. ņŚ┤Ļ░ä ņĢĢņŚ░ ļ¬©ņé¼ĻĖ░ņØĖ Thermocmaster-Zļź╝ ĒÖ£ņÜ®ĒĢśņŚ¼ ņØ╝ņČĢ ņĢĢņČĢ ņŗżĒŚśņØä ņłśĒ¢ēĒĢśņśĆļŗż. ņØ┤ ļĢī, ĻĖ░Ļ│äņØś Ēāäņä▒ļ│ĆĒśĢņ╣śļź╝ ņĀ£Ļ▒░ĒĢśņ¦Ć ļ¬╗ĒĢśņśĆĻĖ░ ļĢīļ¼ĖņŚÉ, ņ¦äļ│ĆĒśĢņ£© Ļ░ÆņØ┤ ņŗżņĀ£ ņ×¼ļŻīĻ░Ć Ļ▓¬ņØĆ ņ¦äļ│ĆĒśĢņ£©ļ│┤ļŗż ļåÆĻ▓ī ļéśĒāĆļéśļŖö ņśżļźśļź╝ ĒżĒĢ©ĒĢ£ļŗż. ļ│┤ļŗż ņ×ÉņäĖĒĢ£ ņŗżĒŚś ļ░®ļ▓ĢņØĆ ņ░ĖĻ│Āļ¼ĖĒŚīņŚÉ ĻĖ░ļĪØļÉśņ¢┤ ņ׳ļŗż [18].
3. Ļ▓░Ļ│╝ ļ░Å Ļ│Āņ░░
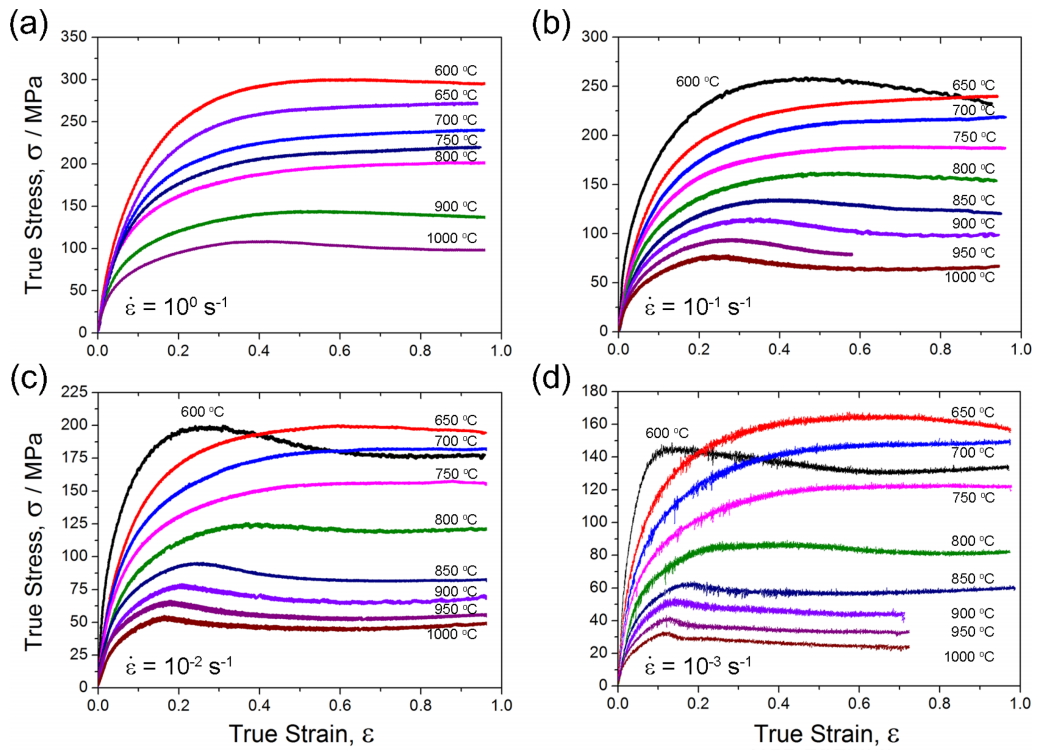
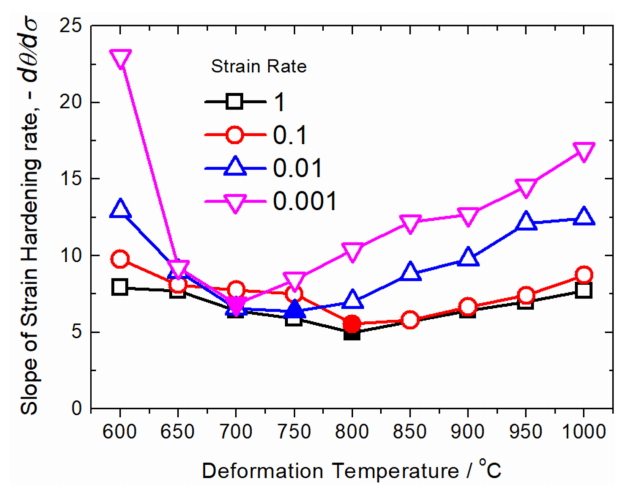
ĻĘĖļ”╝ 1ņØĆ ļŗżņ¢æĒĢ£ ļ│ĆĒśĢņ£© ņåŹļÅäņÖĆ ņĢĢņČĢ ņś©ļÅäņŚÉņä£ ņ¢╗ņØĆ ņ¦äņØæļĀź-ņ¦äļ│ĆĒśĢņ£© Ļ│ĪņäĀņØä ļ│┤ņŚ¼ņżĆļŗż. ņØ╝ļ░śņĀüņ£╝ļĪ£ ļåÆņØĆ ņś©ļÅäņŚÉņä£ļŖö ļé«ņØĆ ņś©ļÅäņŚÉņä£ ļ│ĆĒśĢņØä ĒĢ£ Ļ▓ĮņÜ░ļ│┤ļŗż ņ¦äņØæļĀź Ļ░ÆņØ┤ ļé«Ļ▓ī ļéśĒāĆļé£ļŗż. ļśÉĒĢ£ ļ╣ĀļźĖ ļ│ĆĒśĢņ£© ņåŹļÅäņØś Ļ▓ĮņÜ░ļ│┤ļŗż ļŖÉļ”░ ļ│ĆĒśĢņ£© ņåŹļÅäņØś ņŗżĒŚśņŚÉņä£ ņ¦äņØæļĀź Ļ░ÆņØ┤ ļé«Ļ▓ī ļéśĒāĆļé£ļŗż. ĻĘĖļ”╝ 1ņŚÉņä£ ņĢĢņČĢ ņś©ļÅäĻ░Ć ļåÆĻ▒░ļéś ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć ļŖÉļ”░ Ļ▓ĮņÜ░, ņśżņŖżĒģīļéśņØ┤ĒŖĖļŖö ļÅÖņĀü ņ×¼Ļ▓░ņĀĢņØä Ļ░¢ļŖö ĒśĢĒā£ņØś ņ£ĀļÅÖ ņØæļĀź Ļ│ĪņäĀņØä ļéśĒāĆļé£ļŗż. ņ”ē, ņ┤łĻĖ░ ļ│ĆĒśĢņ£©ņØ┤ ļé«ņØä ļĢīņŚÉļŖö ņ£ĀļÅÖ ņØæļĀźņØ┤ ņ”ØĻ░ĆĒĢśļéś, ņĄ£Ļ│Ā ņØæļĀźņĀÉņŚÉ ļÅäļŗ¼ĒĢ£ Ēøä ļÅÖņĀü ņ×¼Ļ▓░ņĀĢņŚÉ ņØśĒĢ£ ņŚ░ĒÖöĻ░Ć ļéśĒāĆļéśļ®┤ņä£ ņ£ĀļÅÖ ņØæļĀźņØ┤ Ļ░ÉņåīĒĢ£ļŗż. ņØ┤Ēøä ņŚ░ņåŹņĀüņØĖ ļÅÖņĀü ņ×¼Ļ▓░ņĀĢņØ┤ ņØ╝ņ¢┤ļéśļ®┤ņä£ ņ£ĀļÅÖ ņØæļĀźĻ░ÆņØ┤ ņØ╝ņĀĢĒĢśĻ▓ī ĒżĒÖöļÉ£ Ļ░ÆņØä ļ│┤ņØĖļŗż [1,2]. ļ│ĆĒśĢ ņś©ļÅäĻ░Ć Ļ░ÉņåīĒĢśļ®┤ņä£ ņØ┤ļ¤¼ĒĢ£ ņŚ░ĒÖö ĒśäņāüņØ┤ ļŗżņåī ĻĄ¼ļČäņØ┤ ņל ļÉśņ¦Ć ņĢŖļŖö ĻĄ¼Ļ░äņØ┤ ļéśĒāĆļéśļŖöļŹ░, ņØ┤ļŖö ņśżņŖżĒģīļéśņØ┤ĒŖĖņØś ļÅÖņĀü ņ×¼Ļ▓░ņĀĢņØ┤ ņĀÉņ░©ņĀüņ£╝ļĪ£ ņØ╝ņ¢┤ļéśņ¦Ć ņĢŖĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ņØ┤ļ¤¼ĒĢ£ ĒśäņāüņØĆ ņś©ļÅäĻ░Ć ļé«ņĢäņ¦Ćļ®┤ņä£ ņāØĻĖĖ ļ┐Éļ¦ī ņĢäļŗłļØ╝, ļÅÖņØ╝ĒĢ£ ņś©ļÅäņŚÉņä£ ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć ļ╣©ļØ╝ņ¦Ćļ®┤ņä£ļÅä ĒĢ©Ļ╗ś ņØ╝ņ¢┤ļé£ļŗż. ņØ┤ļ¤¼ĒĢ£ ĒśäņāüņŚÉ ļīĆĒĢ┤ņä£ļŖö ĻĘĖļ”╝ 3ņŚÉņä£ ļ│┤ļŗż ņ×ÉņäĖĒĢśĻ▓ī ņäżļ¬ģĒĢ£ļŗż. ĒĢ£ĒÄĖ, ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć ļŖÉļ”¼ļ®┤ņä£ ņś©ļÅäļÅä ļé«ņØĆ Ļ▓ĮņÜ░, ņ£ĀļÅÖ ņØæļĀź Ļ│ĪņäĀņŚÉņä£ ļÜ£ļĀĘĒĢ£ ņŚ░ĒÖöĻ░Ć ļéśĒāĆļéśļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. ņØ┤ļŖö ļÅÖņĀü ņāüļ│ĆĒā£ņŚÉ ņØśĒĢ£ Ļ▓āņ£╝ļĪ£ ņśżņŖżĒģīļéśņØ┤ĒŖĖĻ░Ć ĒÄśļØ╝ņØ┤ĒŖĖļĪ£ ļ░öļĆīļ®┤ņä£, Ļ│Āņś©ņŚÉņä£ Ļ░ĢļÅäĻ░Ć ļé«ņØĆ ĒÄśļØ╝ņØ┤ĒŖĖ ņāüļČäņ£© ņ”ØĻ░ĆņŚÉ ļö░ļźĖ ņŚ░ĒÖöļĪ£ ņØ┤ĒĢ┤ĒĢĀ ņłś ņ׳ļŗż [18,23]. ļ░śļ®┤, ņś©ļÅäĻ░Ć ļé«ņ£╝ļ®┤ņä£ ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć ļ╣ĀļźĖ Ļ▓ĮņÜ░, ņ£ĀļÅÖ ņØæļĀźņØ┤ ņĄ£ļīĆĻ░ÆņØä ļ│┤ņØĖ Ēøä, ņŚ░ĒÖöļź╝ ĒåĄĒĢ£ Ļ░ÉņåīĻ░Ć ĒÖĢņŚ░ĒĢśĻ▓ī ļéśĒāĆļéśņ¦Ć ņĢŖņĢśļŗż. ņØ┤ļŖö ņåīņä▒ ļ│ĆĒśĢ ņŗ£Ļ░äņØ┤ ļČĆņĪ▒ĒĢśņŚ¼, ĒÄśļØ╝ņØ┤ĒŖĖļĪ£ņØś ņāüļ│ĆĒā£Ļ░Ć ņČ®ļČäĒĢ£ ļ░£ņāØĒĢśņ¦Ć ņĢŖņĢä ņØæļĀź ņ£ĀļÅÖ Ļ│ĪņäĀņŚÉ ĒÖĢņŚ░ĒĢśĻ▓ī ļéśĒāĆļéśņ¦Ć ņĢŖņĢśĻĖ░ ļĢīļ¼ĖņØ┤ļŗż [18].
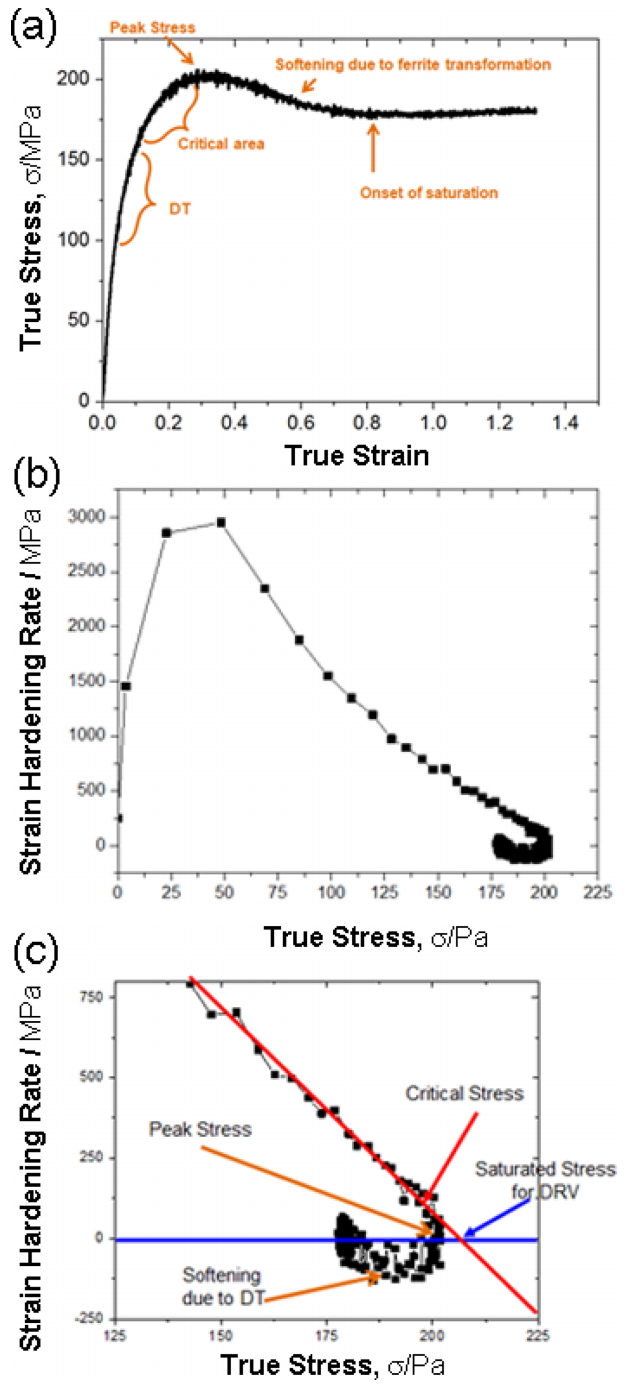
ĻĘĖļ”╝ 2ļŖö ĻĘĖļ”╝ 1ņŚÉņä£ ļéśĒāĆļé£ ņ£ĀļÅÖ ņØæļĀź Ļ│ĪņäĀņØä ĒĢ┤ņäØĒĢśĻ│Āņ×É ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć 0.01 s-1ņØ┤ļ®░, ļ│ĆĒśĢ ņś©ļÅäĻ░Ć 600ļÅäņØĖ ņĪ░Ļ▒┤ņØś ņØæļĀź ņ£ĀļÅÖ Ļ│ĪņäĀņØä ņäĀĒāØĒĢśņśĆļŗż. ĻĘĖļ”╝ 2aņØś ņ£ĀļÅÖ ņØæļĀź Ļ│ĪņäĀņØä ļ│ĆĒśĢņ£©ļĪ£ ļ»ĖļČäĒĢ£ Ļ░ÆņØĆ ņØ╝ļ░śņĀüņ£╝ļĪ£ ļ│ĆĒśĢĻ▓ĮĒÖöņ£©(strain hardening rate, ╬Ė = dŽāŌüä d╬Ą)ļĪ£ ļ¬ģļ¬ģĒĢ£ļŗż (ĻĘĖļ”╝ 2b, ĻĘĖļ”╝ 2c). ĻĘĖļ”╝ 2b ņśüņŚŁņŚÉņä£ ņ¦äņØæļĀźņØ┤ ļ╣äĻĄÉņĀü ļåÆņØĆ 150 MPaņØ┤ņāüņØĖ ņśüņŚŁņØä ĒÖĢļīĆĒĢśņŚ¼ ĻĘĖļ”╝ 2cņŚÉ Ēæ£ņŗ£ĒĢśņśĆļŗż. ĻĘĖļ”╝ 2aņÖĆ ĻĘĖļ”╝ 2cļź╝ ĒĢ©Ļ╗ś ļ│┤ļ®┤, ņØæļĀźņØ┤ ņ”ØĻ░ĆĒĢĀņłśļĪØ ļ│ĆĒśĢņ£© Ļ▓ĮĒÖö Ļ░ÆņØ┤ Ļ░ÉņåīĒĢśļŗżĻ░Ć ņĄ£ļīĆ ņØæļĀźņŚÉ ļÅäļŗ¼ĒĢśĻ▓ī ļÉśļ®┤ ĻĘĖ Ļ░ÆņØ┤ 0ņŚÉ ņłśļĀ┤ĒĢśĻ▓ī ļÉ£ļŗż. ņ”ē, ļ│ĆĒśĢņŚÉ ņØśĒĢ£ Ļ▓ĮĒÖöļÉśļŖö ņ¢æĻ│╝ ļÅÖņĀü ņāüļ│ĆĒā£ Ēś╣ņØĆ ļÅÖņĀü ĒÜīļ│ĄņŚÉ ņØśĒĢ£ ņŚ░ĒÖöļÉśļŖö ņ¢æņØ┤ Ļ░ÖņĢäņ¦ĆļŖö ņĀÉņØ┤ļŗż. ņØ┤Ēøä ņ¦ĆņåŹņĀüņØĖ ļ│ĆĒÖöļŖö ļÅÖņĀü ņāüļ│ĆĒā£ ņ¢æņØä ņ”ØĻ░Ćņŗ£ņ╝£ ņŚ░ĒÖöĻ░Ć ĻĖēĻ▓®Ē׳ ņ”ØĻ░ĆĒĢśļ®░, ņØ┤Ēøä ļ│ĆĒśĢļ¤ēņØ┤ ņĢĮ 0.8 (ĻĘĖļ”╝2a) ņłśņżĆņŚÉņä£ ĒżĒÖöļÉ£ ņ£ĀļÅÖ ņØæļĀźņØä ļ│┤ņØĖļŗż. ĻĖ░ņĪ┤ņØś ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņĄ£ļīĆ ņ£ĀļÅÖ ņØæļĀźĻ░Æ(peak stress)ņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņ£ĀļÅÖ ņØæļĀź Ļ│ĪņäĀ ļČäņäØņØä ņŗżņŗ£ĒĢśņśĆņ£╝ļéś, ņØ┤ļŖö 10% ņØ┤ņāüņØś ļÅÖņĀü ņ×¼Ļ▓░ņĀĢ Ēś╣ņØĆ ļÅÖņĀü ņāüļ│ĆĒā£Ļ░Ć ļ░£ņāØĒĢ£ ņāüĒÖ®, ņ”ē ļÅÖņĀü ņŚ░ĒÖö ņ×æņÜ®ņØ┤ ļ│ĖĻ▓®ņĀüņ£╝ļĪ£ ļéśĒāĆļé£ ņØ┤ĒøäņØś Ļ▓░Ļ│╝ņØ┤ĻĖ░ ļĢīļ¼ĖņŚÉ, ĒÖĢņŗżĒĢ£ ņĀÉņØ┤ĻĖ┤ ĒĢśļéś, ļ»╝Ļ░ÉĒĢśĻ▓ī Ļ░Éņ¦ĆĒĢśņ¦Ć ļ¬╗ĒĢśļŗżļŖö ļŗ©ņĀÉņØ┤ ņ׳ņŚłļŗż [18]. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ļ│┤ļŗż ļ»╝Ļ░ÉĒĢśĻ▓ī ļÅÖņĀü ņŚ░ĒÖö ĒśäņāüņØä Ļ┤Ćņ░░ĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ļÅÖņĀü ņ×¼Ļ▓░ņĀĢ Ēś╣ņØĆ ļÅÖņĀü ņāüļ│ĆĒā£Ļ░Ć ļ░£ņāØĒĢśņ¦Ć ņĢŖņĢśņØä Ļ▓āņ£╝ļĪ£ ņČöņĀĢļÉśļŖö ļČĆļČäņØĖ ņ┤łĻĖ░ ņåīņä▒ ĻĄ¼Ļ░äņŚÉņä£ļČĆĒä░ ņ×äĻ│äņĀÉ(critical point)Ļ╣īņ¦ĆņØś ņØæļĀź ņ£ĀļÅÖ Ļ│ĪņäĀņØä ĒÖ£ņÜ®ĒĢśņŚ¼ ļČäņäØņØä ņŗżņŗ£ĒĢśņśĆļŗż.
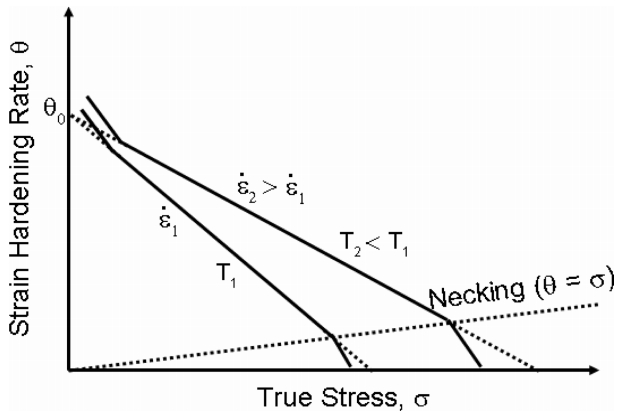
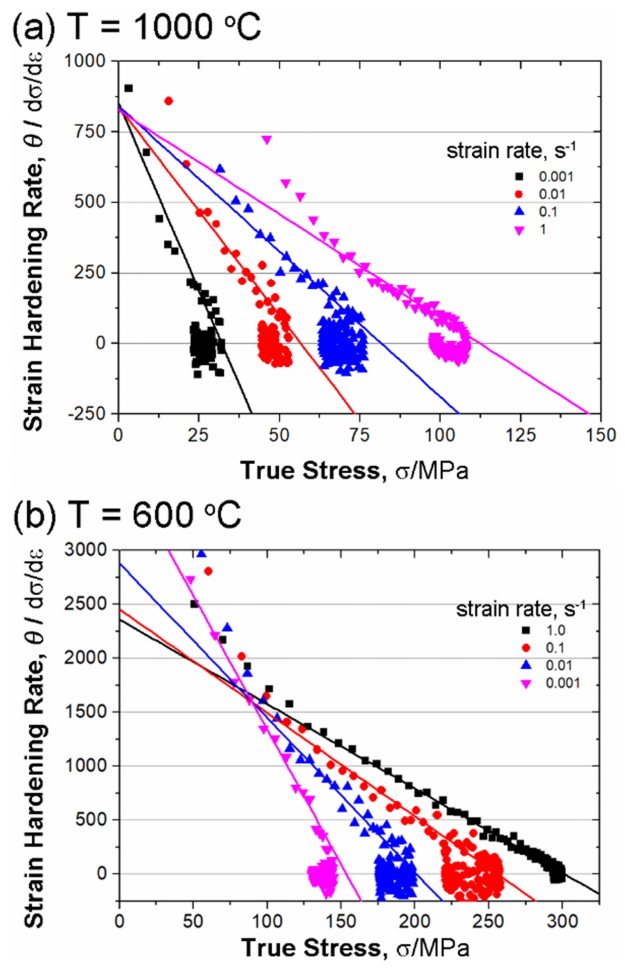
ĻĘĖļ”╝ 3ņØĆ Kocks-MeckingņØś ļ¬©ļŹĖ[3]ņØä ļ░öĒāĢņ£╝ļĪ£ EstrinĻ│╝ MeckingņØ┤ ņĀ£ņĢł[5]ĒĢ£ ĒśĢĒā£ņØś ĻĘĖļ”╝ņØ┤ļŗż. ņÜ░ņäĀ, ņ¦äņØæļĀźņØ┤ ļé«ņØĆ ļČĆļČäņŚÉņä£ņØś ņĀÉņäĀĻ│╝ ņŗżņäĀņØ┤ ļ¦īļéśļŖö ņĀÉņØĆ ņ×¼ļŻīņŚÉņä£ ņĀäņ£äĻ░Ć ļ░£ņāØĒĢśĻĖ░ ņŗ£ņ×æĒĢśļŖö ņĀÉņ£╝ļĪ£, ļŗżĻ▓░ņĀĢņ¦łņØś ĻĖłņåŹņ×¼ļŻīņŚÉņä£ ņŻ╝ļĪ£ ņ¢ĖĻĖēļÉśļŖö ĒĢŁļ│Ą Ēśäņāü Ēś╣ņØĆ ļ│ĆĒśĢ stage IIIņØś ņŗ£ņ×æņĀÉĻ│╝ ļÅÖņØ╝ĒĢ£ Ļ░£ļģÉņ£╝ļĪ£ ņØ┤ĒĢ┤ĒĢĀ ņłś ņ׳ļŗż. ĻĘĖ ņØ┤Ēøä Ļ░ĢļÅäĻ░Ć ļåÆņĢäņ¦Ćļ®┤ņä£ ņØ╝ņĀĢĒĢśĻ▓ī ļ│ĆĒśĢĻ▓ĮĒÖöņ£©ņØ┤ Ļ░ÉņåīĒĢśļŖö ĻĄ¼Ļ░äņØĆ ņåīņä▒ ļ│ĆĒśĢņŚÉ ņØśĒĢ£ ņĀäņ£ä ņ”ØņŗØĻ│╝ ļÅÖņĀü ĒÜīļ│ĄņŚÉ ņØśĒĢ£ ņŚ░ĒÖöņØś ļ╣äņ£©ņØ┤ ņØ╝ņĀĢĒĢśĻ▓ī ļ░öļĆīļŖö ĻĄ¼Ļ░äņØ┤ļŗż. ņØ┤Ēøä Ļ▓ĮĒÖöņŚÉ ņØśĒĢ£ ņØæļĀźņØ┤ ņ¦ĆņåŹņĀüņ£╝ļĪ£ ļåÆņĢäņ¦ĆĻ│Ā, ņØ┤ ņØæļĀźĻ░ÆņØ┤ ļ│ĆĒśĢĻ▓ĮĒÖöņ£©Ļ│╝ Ļ░ÖņĢäņ¦ĆļŖö ņåīņä▒ ļČłņĢłņĀĢņĀÉ(plastic instability, Žā = dŽāŌüä d╬Ą = ╬Ė)ņØ┤ ļ░£ņāØļÉśļŖö ņĀÉ(necking)ņØ┤ ļéśĒāĆļé£ļŗż. ņØ┤ Ļ░ÆņØä ļäśņ¢┤ņä£, ņŚ░ĒÖö ņåŹļÅäĻ░Ć ļ│ĆĒśĢĻ▓ĮĒÖöņ£©ļ│┤ļŗż Ēø©ņö¼ ļ╣©ļØ╝ņ¦ĆĻ▓ī ļÉśļŖö ĻĄ¼Ļ░äņØ┤ ļéśĒāĆļéśļ®░, ņØ┤ļŖö ĻĘĖļ”╝ 3ņŚÉņä£ ļ│ĆĒśĢĻ▓ĮĒÖöņ£©ņØ┤ 0ņŚÉ Ļ░ĆĻ╣ØĻ▓ī Ļ░ĆļŖö ĻĄ¼Ļ░äņØ┤ļŗż. ļ│ĆĒśĢĻ▓ĮĒÖöņ£©ņØ┤ 0ņØ┤ ļÉśļŖö ņĀÉņØĆ ĻĘĖļ”╝ 2ņŚÉņä£ ņĄ£ļīĆ ņ£ĀļÅÖ ņØæļĀź(peak stress)ņŚÉ ļīĆņØæļÉ£ļŗż. ļśÉĒĢ£, ņ£ĀļÅÖ ņØæļĀź Ļ│ĪņäĀņØä ĒĢ┤ņäØĒĢĀ ļĢī, ļÅÖņØ╝ĒĢ£ ņØæļĀź ĒĢśņŚÉņä£ ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć ļ╣ĀļźĖ ļ│ĆĒśĢĻ▓ĮĒÖöņ£© Ļ░ÆņØ┤ ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć ļŖÉļ”░ ļ│ĆĒśĢĻ▓ĮĒÖöņ£© Ļ░Æļ│┤ļŗż ļåÆļŗżļŖö Ļ▓āņØä ļ│┤ņŚ¼ņżĆļŗż. ļ¦łņ░¼Ļ░Ćņ¦ĆļĪ£ ņś©ļÅäņØś ļ│ĆĒÖöņŚÉ ļīĆĒĢ┤ ņØ┤ĒĢ┤ĒĢĀ ņłś ņ׳ļŗż. ņś©ļÅäņÖĆ ļ│ĆĒśĢņ£© ņåŹļÅä, ļæÉ ļ│ĆņłśņŚÉ ļīĆĒĢ£ ņśüĒ¢źņØä ļÅÖņŗ£ņŚÉ ĒĢ┤ņäØĒĢśĻĖ░ ņ£äĒĢśņŚ¼, Ēü¼ļ”Į(creep)ņŚÉņä£ ņŻ╝ļĪ£ ļ¦ÄņØ┤ ĒÖ£ņÜ®ļÉśļŖö Zener-Hollomon Ļ┤ĆĻ│äņŗØņØä ļÅäņ×ģĒĢ£ļŗż.
╬Ą ļŖö ļ│ĆĒśĢņ£© ņåŹļÅä, Q ļŖö Ļ▓ēļ│┤ĻĖ░ ĒÖ£ņä▒ĒÖö ņŚÉļäłņ¦Ć, R ņØĆ ĻĖ░ņ▓┤ ņāüņłś, ĻĘĖļ”¼Ļ│Ā T ņĀłļīĆ ņś©ļÅäņØ┤ļŗż. ĒÖ£ņä▒ĒÖö ņŚÉļäłņ¦ĆļŖö ņøÉņ×ÉņØś ņ×¼ņĀĢļĀ¼ņØ┤ ņ¢╝ļ¦łļéś ņēĮĻ▓ī Ēś╣ņØĆ ņ¢┤ļĀĄĻ▓ī ļ░£ņāØĒĢśļŖöņ¦Ćļź╝ ļ│┤ņŚ¼ņŻ╝ļŖö ņØĖņ×ÉļĪ£, ņŻ╝ļĪ£ ņ£©ņåŹ ĻĖ░ĻĄ¼ņŚÉ ļīĆĒĢ£ Ļ░ÆņØä ļéśĒāĆļéĖļŗż. Ēü¼ļ”Į ĒÅēĻ░Ćļź╝ ĒåĄĒĢ┤ ņ¢╗ņØĆ ĒÖ£ņä▒ĒÖö ņŚÉļäłņ¦ĆļŖö ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ ĒÖ£ņÜ®ĒĢ£ ņĢĢņČĢņŗżĒŚśņŚÉņä£ ņ¢╗ņØĆ Ļ░Æļ│┤ļŗż ņØ╝ļ░śņĀüņ£╝ļĪ£ ļé«Ļ▓ī ļéśĒāĆļéśļ®░, ņØ┤ Ļ░ÆņØĆ ņøÉņ×ÉņØś ņ×ÉĻĖ░ ĒÖĢņé░ ņŚÉļäłņ¦ĆņÖĆ ņ£Āņé¼ĒĢ£ Ļ░ÆņØä Ļ░¢ļŖöļŗż. ņ”ē, Ļ│ĄĻ│ĄņØś ĒśĢņä▒Ļ│╝ ņØ┤ļÅÖņŚÉ ĒĢäņÜöĒĢ£ ņŚÉļäłņ¦ĆļĪ£, ņ╣╝ļéĀ ņĀäņ£äņØś ņāüņŖ╣ņØ┤ļéś ļéśņé¼ ņĀäņ£äņØś ņĪ░ĻĘĖ ļō▒ņŚÉ ņØśĒĢ┤ ņŻ╝ļĪ£ Ļ▓░ņĀĢļÉ£ļŗż [24]. ĻĘĖļ”╝ 3ņŚÉņä£ ļ│Ė Ļ▓āĻ│╝ Ļ░ÖņØ┤, ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć ļ╣Āļź┤ļŗżļŖö Ļ▓āņØĆ Z Ļ░ÆņØ┤ ņ╗żņ¦ĆļŖö Ļ▓āņØä ņØśļ»ĖĒĢśļ®░, ņØ┤ļŖö ļ¦łņ╣ś ļ│ĆĒśĢ ņś©ļÅäĻ░Ć ļé«ņØĆ Ļ▓āĻ│╝ Ļ░ÖņØĆ ĒÜ©Ļ│╝ļź╝ Ļ░¢ļŖöļŗż. ņśłļź╝ ļōżņ¢┤, ņØĖņן ņŗ£ĒŚś ņŗ£, ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć ļ╣Āļź┤ļ®┤ ņØæļĀźņØĆ ļåÆĻ▓ī ļéśņśżļ®░, ņŗ£ĒŚś ņś©ļÅäĻ░Ć ļé«ņ£╝ļ®┤ ņØæļĀźņØ┤ ļåÆĻ▓ī ļéśņśżļŖö ĒśäņāüĻ│╝ ļÅÖņØ╝ĒĢśĻ▓ī ņØ┤ĒĢ┤ĒĢĀ ņłś ņ׳ļŗż. ĻĘĖļ”╝ 1ņØś ņ£ĀļÅÖ Ļ│ĪņäĀņØä ĻĘĖļ”╝ 3Ļ│╝ Ļ░ÖņØĆ ĒśĢĒā£ļĪ£ ļ│ĆĒÖöņŗ£ņ╝░ņØä ļĢī, ļŗżņ¢æĒĢ£ ļ│ĆĒśĢņ£© ņåŹļÅäņÖĆ ņś©ļÅäņŚÉ ļö░ļØ╝ ļŗżņ¢æĒĢ£ ļ│ĆĒśĢĻ▓ĮĒÖöņ£©ņØä Ļ░Ćņ¦Ćļ®░, ņØ┤ļŖö ņĀæņäĀņØś ĻĖ░ņÜĖĻĖ░ļĪ£ ļéśĒāĆļé£ļŗż. ņØ┤ ĻĖ░ņÜĖĻĖ░ļŖö ļÅÖņĀüņØĖ Ļ▓ĮĒÖöņÖĆ ņŚ░ĒÖöņØś ĒĢ®ņ£╝ļĪ£ Ļ▓░ņĀĢļÉśļŖö Ļ▓āņ£╝ļĪ£, ļ│ĆĒśĢĻ▓ĮĒÖöņ£©Ļ│╝ ļÅÖņĀü ĒÜīļ│Ąņ£©ņØś ņ░©ņØ┤ļĪ£ Ēæ£ĒśäĒĢĀ ņłś ņ׳ļŗż [4]. ņØ┤ ĻĖ░ņÜĖĻĖ░ļŖö Zener-Hollomon Ļ┤ĆĻ│äņŚÉ ņóģņåŹļÉśņ¢┤ ļ│ĆĒśĢ ņś©ļÅäņÖĆ ļ│ĆĒśĢņ£© ņåŹļÅäņŚÉ Ļ░ĢĒĢśĻ▓ī ņØśņĪ┤ĒĢśļŖöļŹ░, ļ®┤ņŗ¼ ņ×ģļ░® ĻĄ¼ņĪ░ļź╝ Ļ░¢ļŖö ĻĖłņåŹņ×¼ļŻīņÖĆ Ļ░ÖņØ┤ ļ│ĆĒśĢņ£© ņåŹļÅäņÖĆ ļ│ĆĒśĢ ņś©ļÅäņØś ņØśņĪ┤ņä▒ņØ┤ ļé«ņØĆ Ļ▓ĮņÜ░ņŚÉļŖö ņŻ╝ļĪ£ ĒĢśļéśņØś ļ│ĆĒśĢĻ▓ĮĒÖöņ£© ņāüņłśņŚÉ ņłśļĀ┤ĒĢ£ļŗżĻ│Ā ļ│┤Ļ│ĀļÉśĻ│Ā ņ׳ļŗż. [5]. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ļŗżņ¢æĒĢ£ ļ│ĆĒśĢņ£© ņåŹļÅäņÖĆ ļ│ĆĒśĢņś©ļÅäļź╝ ņé¼ņÜ®ĒĢśņśĆĻĖ░ ļĢīļ¼ĖņŚÉ, ĻĘĖļ”╝ 3ņØä ĒåĄĒĢ┤ Zener-Hollomon Ļ┤ĆĻ│äļź╝ ņØ┤ĒĢ┤ĒĢśĻ│Ā, ĻĘĖļ”╝ 4ļź╝ ņēĮĻ▓ī ņØ┤ĒĢ┤ĒĢĀ ņłś ņ׳ļŗż.
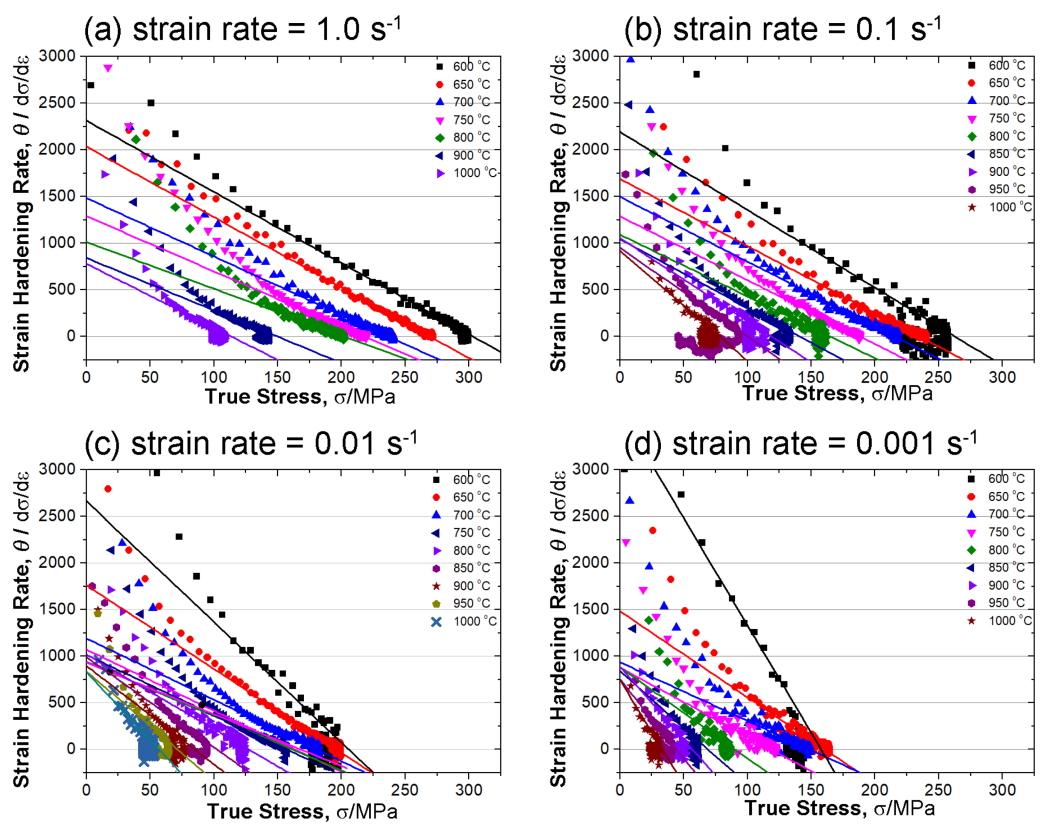
ĻĘĖļ”╝ 4ļŖö ĻĘĖļ”╝ 1ņŚÉņä£ ļéśĒāĆļé£ ņ£ĀļÅÖ ņØæļĀź Ļ│ĪņäĀļōżņØä ņØ┤ņÜ®ĒĢśņŚ¼ ļ│ĆĒśĢĻ▓ĮĒÖöņ£©Ļ│╝ ņ¦äņØæļĀźļĪ£ ļŗżņŗ£ ļéśĒāĆļéĖ Ļ▓āņØ┤ļŗż. ĻĘĖļ”╝ 3ņŚÉņä£ ļ│Ė Ļ▓āĻ│╝ Ļ░ÖņØ┤ ņ¦üņäĀņØ┤ ļéśņśżļŖö ĻĄ¼Ļ░äņØä ĒÖ£ņÜ®ĒĢśņŚ¼ Žć2 ļ╣äĻĄÉ Ēøä ņÖĖņéĮņØä ņŗżņŗ£ĒĢśņśĆļŗż. ĻĘĖļ”╝ 4dņÖĆ Ļ░ÖņØ┤ ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć ļŖÉļ”░ Ļ▓ĮņÜ░, 600ļÅä Ēś╣ņØĆ 650ļÅäļź╝ ņĀ£ņÖĖĒĢ£ Ļ│Āņś© ņŗżĒŚśņØś ņÖĖņéĮĻ░ÆņØ┤ ĻĘĖļ”╝ 3ņŚÉņä£ ļ│Ė Ļ▓āĻ│╝ Ļ░ÖņØ┤ ņäĖļĪ£ņČĢņØś ĒĢ£ ņĀÉ(╬Ė0)ņ£╝ļĪ£ ņłśļĀ┤ĒĢśļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. ╬Ė0ļŖö ņĢĮ 850 MPa ĻĘ╝ņ▓śņ×äņØä ņĢī ņłś ņ׳ļŗż. ļÅÖņĀü ņ×¼Ļ▓░ņĀĢņØ┤ļéś ļÅÖņĀü ņāüļ│ĆĒā£Ļ│╝ Ļ░ÖņØĆ ĻĖēĻ▓®ĒĢ£ ņŚ░ĒÖöĻ░Ć ļ░£ņāØļÉśņ¦Ć ņĢŖļŖöļŗżĻ│Ā Ļ░ĆņĀĢĒĢ£ļŗżļ®┤, ņĢ×ņä£ ņ¢ĖĻĖēĒĢśņśĆļō»ņØ┤ ļŗżņ¢æĒĢ£ ļ│ĆĒśĢĻ▓ĮĒÖöņ£© ņäĀļōżņØś ņŚ░ņןņäĀļōżņØ┤ ĒĢśļéśņØś ļ│ĆĒśĢĻ▓ĮĒÖöņ£© ņāüņłś(╬Ė0)ņŚÉ ņל ņłśļĀ┤ĒĢśļŖö Ļ▓░Ļ│╝ļź╝ ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŗż [5]. ĒĢśņ¦Ćļ¦ī ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć ņĀÉņ░© ļ╣©ļØ╝ņ¦ÉņŚÉ ļö░ļØ╝, ļśÉĒĢ£ ļ│ĆĒśĢ ņś©ļÅäĻ░Ć ļé«ņĢäņ¦Ćļ®┤ņä£ (ņ”ē, Z Ļ░ÆņØ┤ ņ╗żņ¦Ćļ®┤ņä£) ņäĖļĪ£ņČĢņ£╝ļĪ£ ņÖĖņéĮĒĢ£ Ļ░ÆņØ┤ ╬Ė0ņŚÉņä£ ņĀÉņ░© ļ®Ćņ¢┤ņ¦ĆļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. ņśłļź╝ ļōżļ®┤, ĻĘĖļ”╝ 4aņØś Ļ▓ĮņÜ░, Ļ│Āņś© ņĢĢņČĢņØĖ 1000ļÅäņŚÉņä£ 850ļÅä ņĀĢļÅäņØś ņŗżĒŚśņŚÉņä£ ļéśĒāĆļé£ ╬Ė0ņØ┤ ņĢĮ 750~1000 MPaņØ┤ņ¦Ćļ¦ī, ĻĘĖ ņØ┤ĒĢśņØś ņś©ļÅäņŚÉņä£ ļéśĒāĆļéśļŖö Ļ░ÆņØĆ ļ¦żņÜ░ ļåÆĻ▓ī ļéśĒāĆļé£ Ļ▓āņØä ņĢī ņłś ņ׳ļŗż. ņØ┤ļĀćĻ▓ī ĻĖēĻ▓®ĒĢ£ ĻĖ░ņÜĖĻĖ░ņØś ļ│ĆĒÖöĻ░Ć ņāØĻĖ░ļŖö ņØ┤ņ£ĀļŖö ļÅÖņĀü ĒÜīļ│ĄņŚÉ ņØśĒĢ┤ ņŚ░ĒÖöļÉśļŖö ņåŹļÅäļ│┤ļŗż ņāüļīĆņĀüņ£╝ļĪ£ ļ╣ĀļźĖ ļ│ĆĒśĢĻ▓ĮĒÖöņ£©ņØś ņ”ØĻ░ĆļĪ£ ļéśĒāĆļé£ Ļ▓░Ļ│╝ņØ┤ļŗż. ņ”ē, ņśżņŖżĒģīļéśņØ┤ĒŖĖ ļé┤ļČĆņØś ņĀäņ£äĻ░Ć ĻĖēĻ▓®ĒĢśĻ▓ī ņ”ØņŗØļÉ£ Ļ▓░Ļ│╝ņØ┤Ļ▒░ļéś ļÅÖņĀü ņāüļ│ĆĒā£ņØś Ļ▓░Ļ│╝ņØ┤ļŗż. Ļ▓░ĻĄŁ, ļåÆņØĆ ļ│ĆĒśĢņ£© ņåŹļÅäņÖĆ ļé«ņØĆ ļ│ĆĒśĢ ņś©ļÅäņÖĆ Ļ░ÖņØĆ ĒŖ╣ņĀĢ ņĪ░Ļ▒┤ņŚÉņä£ ļ│ĆĒśĢņ£© ņåŹļÅäņÖĆ ļ│ĆĒśĢ ņś©ļÅäņŚÉ ļö░ļźĖ ĻĖ░ņÜĖĻĖ░(d╬ĖŌüä dŽā)Ļ░Ć Ēü¼Ļ▓ī ļŗ¼ļØ╝ņ¦ĆļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ņ£╝ļ®░, ņØ┤ļ¤¼ĒĢ£ ļ│ĆĒÖöļź╝ ĻĘĖļ”╝ 5ņŚÉ Ēæ£ņŗ£ĒĢśņśĆļŗż. ņ░ĖĻ│ĀļĪ£, ņŚ¼ĻĖ░ņä£ ņĀłļīĆĻ░ÆņŚÉ ļīĆĒĢ┤ ņŻ╝ņØśĒĢ┤ņĢ╝ ĒĢĀ ņé¼ĒĢŁņØ┤ ņ׳ņØīņØä ļ░ØĒ×īļŗż. Ēśäņ×¼ ļ│┤ņŚ¼ņŻ╝Ļ│Ā ņ׳ļŖö Ļ░ÆļōżņØĆ ņĢ×ņä£ ņ¢ĖĻĖēĒĢśņśĆļō»ņØ┤ ĻĖ░Ļ│ä ņśżļźśļź╝ ĒżĒĢ©ĒĢśĻ│Ā ņ׳ļŗż. ļŗżņŗ£ ļ¦ÉĒĢ┤, ņĢĢņČĢ ņŗżĒŚś ņŗ£, ņ¢╗ņØĆ ļ│ĆĒśĢņ£©ņØĆ ņŗżņĀ£ ņ×¼ļŻīņØś ļ│ĆĒśĢņ£©ļ¦ī Ēæ£ĒśäļÉ£ Ļ▓āņØ┤ ņĢäļŗłļØ╝, ņŚ┤Ļ░ä ņĢĢņŚ░ ļ¬©ņé¼ĻĖ░ņØĖ Thermocmaster-ZņŚÉņä£ ņśżļŖö Ēāäņä▒ ļ│ĆĒśĢļ¤ēļÅä ĒżĒĢ©ĒĢśĻ│Ā ņ׳ļŗż. ņØ┤ ļ│ĆĒśĢļ¤ēņØä ņØ┤ņÜ®ĒĢśņŚ¼ ļ│ĆĒśĢĻ▓ĮĒÖöņ£©ņØä ĻĄ¼ĒĢ£ Ļ░ÆņØä Ēśäņ×¼ ĒÖ£ņÜ®ĒĢśĻ│Ā ņ׳ĻĖ░ ļĢīļ¼ĖņŚÉ ĻĘĖļ”╝ 4ņŚÉņä£ ņäĖļĪ£ņČĢņŚÉ ļéśĒāĆļé£ ņĀłļīĆĻ░ÆņØĆ ņŗĀļó░ĒĢĀ ņłś ņŚåļŗż. ĒĢśņ¦Ćļ¦ī ļ│ĆĒÖöņØś Ļ▓ĮĒ¢źņØä ņØ┤ĒĢ┤ĒĢ©ņŚÉ ņ׳ņ¢┤ņä£ ļČĆņĪ▒ĒĢśņ¦Ć ņĢŖļŗż.
ĻĘĖļ”╝ 5ļŖö ĻĘĖļ”╝ 4ņŚÉņä£ ļéśņś© ĻĖ░ņÜĖĻĖ░ņØś ņØīņØś Ļ░Æ(ŌĆōd╬ĖŌüä dŽā)ņ£╝ļĪ£ Ēæ£ņŗ£ĒĢśņśĆļŗż. Ļ░ü ļ│ĆĒśĢņ£© ņåŹļÅäļ│äļĪ£ ņóīņÜ░ ļæÉ Ļ░£ņØś ĻĄ¼Ļ░äņ£╝ļĪ£ ļéśļłĀ ĒĢ┤ņäØĒĢĀ ņłś ņ׳ļŗż. ĻĘĖļ”╝ 1ņŚÉņä£ ļ│Ė Ļ▓āĻ│╝ Ļ░ÖņØ┤ ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć ļŖÉļ”¼ļ®┤ņä£ Ļ│Āņś©ņØĖ Ļ▓ĮņÜ░, ņśżņŖżĒģīļéśņØ┤ĒŖĖņØś ļÅÖņĀü ņ×¼Ļ▓░ņĀĢņØ┤ ļ░£ņāØĒĢśņśĆļŗż. ļ│ĆĒśĢ ņś©ļÅäĻ░Ć ļé«ņĢäņ¦Ćļ®┤ņä£ ĻĘĖļ”╝ 5ņØś Ļ░ÆņØ┤ ņĀÉņ░© ļé«ņĢäņ¦ĆļŗżĻ░Ć ļŗ½Ē×ī Ēæ£ņŗ£(Ō¢ĀŌŚÅŌ¢▓Ō¢╝)ļź╝ ĒĢ£ ņś©ļÅä ņØ┤ĒĢśņŚÉņä£ļČĆĒä░ļŖö ĻĘĖ Ļ░ÆņØ┤ ņś¼ļØ╝Ļ░ĆļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. ņØ┤ ļČĆļČäņŚÉņä£ļŖö ņśżņŖżĒģīļéśņØ┤ĒŖĖņØś ļÅÖņĀü ņ×¼Ļ▓░ņĀĢņØ┤ ņĢäļŗī ĒÄśļØ╝ņØ┤ĒŖĖļĪ£ņØś ļÅÖņĀü ņāüļ│ĆĒā£Ļ░Ć ļéśĒāĆļéśļŖö ĻĄ¼Ļ░äņ£╝ļĪ£, ļŗ½Ē×ī Ēæ£ņŗ£ļź╝ ĒĢ£ ļČĆļČäņØ┤ ļ░öļĪ£ Ļ░ü ļ│ĆĒśĢņ£© ņåŹļÅäņŚÉņä£ ļÅÖņĀü ņāüļ│ĆĒā£Ļ░Ć ļ░£ņāØĒĢĀ ņłś ņ׳ļŖö ņĄ£ļīĆ ņś©ļÅäĻ░Ć ļÉśļŖö Ļ▓āņØä ņĢī ņłś ņ׳ļŗż. ĒĢ£ĒÄĖ ĒĢ┤ļŗ╣ ņś©ļÅäļ│┤ļŗż ļé«ņØĆ Ļ▓ĮņÜ░, ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć ļŖÉļĀĖņØä ļĢīņØś ĻĖ░ņÜĖĻĖ░(Ō¢Į)Ļ░Ć ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć ļ╣©ļ×ÉņØä ļĢīņØś ĻĖ░ņÜĖĻĖ░(Ō¢Ī)ļ│┤ļŗż Ēü¼Ļ▓ī ņāüņŖ╣ĒĢśļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. ņØ┤ļŖö ļ│ĆĒśĢņ£© ņåŹļÅäņŚÉ ļö░ļźĖ ņĀäņ▓┤ņĀüņØĖ ļ│ĆĒśĢņŗ£Ļ░äņØ┤ ĻĖĖņ¢┤ņĪīĻĖ░ ļĢīļ¼ĖņŚÉ, ļÅÖņĀüņ£╝ļĪ£ ņāüļ│ĆĒā£Ļ░Ć ļ░£ņāØĒĢśļŖö ļČäņ£©ņØ┤ Ēü¼Ļ▓ī ņ”ØĻ░ĆĒĢśņśĆĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ļ╣äļĪØ ņĄ£ļīĆ ņ£ĀļÅÖ ņØæļĀźĻ╣īņ¦Ć ļÅäļŗ¼ĒĢśĻĖ░ ņĀäņØś ņāüĒā£ļĪ£ ļČäņäØņØä ĒĢśĻ│Ā ņ׳ņØīņŚÉļÅä ļČłĻĄ¼ĒĢśĻ│Ā ņØ┤ļĀćĻ▓ī Ēü¼Ļ▓ī Ļ░ÆņØ┤ ļ░öļĆīļŖö Ļ▓āņØĆ ņØ┤ļ»Ė ņāüļŗ╣ļ¤ēņØś ļÅÖņĀü ņāüļ│ĆĒā£Ļ░Ć ņĄ£ļīĆ ņ£ĀļÅÖ ņØæļĀź ņĀäņŚÉ ļ░£ņāØĒĢśĻ│Ā ņ׳ņØīņØä ņØśļ»ĖĒĢ£ļŗż.
ļ│Ė ņŚ░ĻĄ¼ļź╝ ĒåĄĒĢ┤ņä£ ļ░£Ļ▓¼ĒĢ£ ļ¦żņÜ░ ĒØźļ»ĖļĪ£ņÜ┤ ņĀÉņØĆ ļÅÖņĀü ņāüļ│ĆĒā£ Ēś╣ņØĆ ļÅÖņĀü ņ×¼Ļ▓░ņĀĢņØä ņØ╝ņ£╝ĒéżĻĖ░ ņ£äĒĢ£ ĻĄ¼ļÅÖ ņŚÉļäłņ¦ĆĻ░Ć ļ¦żņÜ░ ļŗżļź┤ļŗżļŖö Ļ▓āņØ┤ļŗż. Ēśäņ×¼ ļČäņäØĒĢ£ Ļ│ĪņäĀņØś ņ£ĀļÅÖ ņØæļĀź Ļ│ĪņäĀņØś ņ┤łĻĖ░Ļ░ÆņØĆ ņśżņŖżĒģīļéśņØ┤ĒŖĖ ņ×ģņןņŚÉņä£ņØś ļÅÖņĀü ĒÜīļ│ĄņŚÉ ĒĢ┤ļŗ╣ļÉśļŖö ĻĄ¼Ļ░äņØ┤ļŗż. ņØ┤ļ»Ė ņל ņĢīļĀżņ¦ä ļ░öņÖĆ Ļ░ÖņØ┤, ņåīņä▒ ņ┤łĻĖ░ ļŗ©Ļ│äņŚÉņä£ ļÅÖņĀü ĒÜīļ│ĄņØ┤ ļéśĒāĆļéśņ¦Ćļ¦ī, ņĪ░ĻĖł ļŹö ļ¦ÄņØĆ ņåīņä▒ņØ┤ Ļ░ĆĒĢ┤ņ¦ł Ļ▓ĮņÜ░, ļÅÖņĀü ĒÜīļ│Ąļ¦īņ£╝ļĪ£ ņČ®ļČäĒ׳ ĒĢ┤ņåīĻ░Ć ļÉśņ¦Ć ņĢŖņØĆ ņĀäņ£äļōżņØ┤ ņīōņØ┤ļ®░, ņ×äĻ│äņĀÉ ņØ┤ņāü ļłäņĀüļÉśļŖö ņŚÉļäłņ¦ĆĻ░Ć ļ░öļĪ£ ļÅÖņĀü ņ×¼Ļ▓░ņĀĢņØä ņ£äĒĢ£ ĻĄ¼ļÅÖļĀźņ£╝ļĪ£ ņ×æņÜ®ĒĢ£ļŗż. ĒĢśņ¦Ćļ¦ī ĻĘĖļ”╝ 4ņŚÉņä£ņÖĆ Ļ░ÖņØ┤ ļ│ĆĒśĢĻ▓ĮĒÖöņ£© ĻĖ░ņÜĖĻĖ░ Ļ░ÆņØ┤ Ēü¼Ļ▓ī ļŗ¼ļØ╝ņ¦ĆļŖö ļÅÖņĀü ņāüļ│ĆĒā£ņØś Ļ▓ĮņÜ░, ņśżņŖżĒģīļéśņØ┤ĒŖĖņØś ļÅÖņĀü ņ×¼Ļ▓░ņĀĢļ¦īĒü╝ ļ¦ÄņØĆ ņåīņä▒ņØ┤ ņÜöĻĄ¼ļÉśņ¦Ć ņĢŖĻ│ĀļÅä ļÅÖņĀü ņāüļ│ĆĒā£Ļ░Ć ļ░£ņāØĒĢśļ®░, ņ×äĻ│äņĀÉņŚÉ ļÅäļŗ¼ĒĢśĻĖ░ ņĀäņŚÉ ļÅÖņĀü ņāüļ│ĆĒā£ļĪ£ ņØĖĒĢ£ ĒÄśļØ╝ņØ┤ĒŖĖ ļČäņ£©ņØ┤ ņØ┤ļ»Ė ņłś ĒŹ╝ņä╝ĒŖĖ ņĪ┤ņ×¼ĒĢĀ Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ĒĢĀ ņłś ņ׳ļŗż. ņØ┤ļĀćĻ▓ī ļéśĒāĆļé£ ĒÄśļØ╝ņØ┤ĒŖĖļŖö 2ņ░© ņāüņ£╝ļĪ£ņŹ© ņ×¼ļŻīļź╝ Ļ░ĢĒÖöņŗ£ĒéżļŖö ņŚŁĒĢĀņØä ĒĢśĻ▓ī ļÉśļ®░, ņØ┤ļĪ£ ņØĖĒĢśņŚ¼ ņ¦ĆņåŹņĀüņ£╝ļĪ£ ļåÆņØĆ ļ│ĆĒśĢĻ░ĆĻ│Ąņ£© Ļ░ÆņØä ļ│┤ņØĖļŗżĻ│Ā ĒīÉļŗ©ĒĢĀ ņłś ņ׳ļŗż.
ĻĘĖļ”╝ 6ņØĆ ļ│ĆĒśĢ ņś©ļÅä 600ļÅäņŚÉņä£ ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć 0.01 s-1ņØĖ ļ│ĆĒśĢņØä Ļ░ĆĒĢśļŖö ņĪ░Ļ▒┤(ĻĘĖļ”╝ 2 ņ░ĖĻ│Ā)ņŚÉņä£ ļæÉ Ļ░£ņØś ļŗżļźĖ ļ│ĆĒśĢļ¤ē(0.07, 0.29)Ļ╣īņ¦Ć ņåīņä▒ ļ│ĆĒśĢ Ēøä, ĻĖēļāēņŗ£Ēé© ņŗ£ĒÄĖņØś ļ»ĖņäĖņĪ░ņ¦üņØä ļ│┤ņŚ¼ņżĆļŗż. ņ¦äļ│ĆĒśĢļ¤ēņØ┤ 0.07ņØĖ Ļ▓ĮņÜ░, ĒÄśļØ╝ņØ┤ĒŖĖĻ░Ć ĻĄ¼ ņśżņŖżĒģīļéśņØ┤ĒŖĖ Ļ▓░ņĀĢļ”ĮĻ│ä ņŻ╝ļ│ĆņØä ņ░©ņ¦ĆĒĢśĻ│Ā ņ׳ļŗż. ņØ┤ļŖö ĻĘĖļ”╝ 2ņŚÉņä£ ļ│┤ļō»ņØ┤ ņ┤łĻĖ░ ĒÄśļØ╝ņØ┤ĒŖĖ ĒĢĄņāØņä▒ ĻĄ¼Ļ░äņØ┤ļ®░ ņĄ£ļīĆ ņ£ĀļÅÖ ņØæļĀźņŚÉ ļÅäļŗ¼ĒĢśĻĖ░ ņĀä ņāüĒā£ņØ┤ļŗż. ņåīņä▒ ļ│ĆĒśĢ ņżæ, Ļ░Ćņן ļåÆņØĆ Ļ▓░ĒĢ© ņŚÉļäłņ¦Ćļź╝ Ļ░Ćņ¦ĆļŖö ņśżņŖżĒģīļéśņØ┤ĒŖĖ Ļ▓░ņĀĢļ”ĮĻ│äņŚÉ ĒÄśļØ╝ņØ┤ĒŖĖ ĒĢäļ”ä ĒśĢĒā£ļĪ£ ņāØņä▒ļÉ£ Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż. ņØ┤ļĀćĻ▓ī ņĀüņØĆ ļČĆĒö╝ļČäņ£©ņØś ņ┤łĻĖ░ ĒÄśļØ╝ņØ┤ĒŖĖ ĒĢäļ”äņØś ĒśĢņä▒ņØ┤ ĻĘĖļ”╝ 4ņÖĆ Ļ░ÖņØ┤ ļ│ĆĒśĢĻ▓ĮĒÖöņ£©ņŚÉ ļ»╝Ļ░ÉĒĢśĻ▓ī ņśüĒ¢źņØä ņżĆļŗżļŖö Ļ▓āņØä ņĢī ņłś ņ׳ļŗż. ņ¦äļ│ĆĒśĢļ¤ēņØ┤ 0.29ņØĖ Ļ▓ĮņÜ░, ņĄ£ļīĆ ņ£ĀļÅÖ ņØæļĀź ņāüĒā£Ļ╣īņ¦Ć ļÅäļŗ¼ĒĢśņśĆņ£╝ļ®░, ņØ┤ ļĢī ņØ┤ļ»Ė ļÅÖņĀü ņŚ░ĒÖöĻ░Ć ļŗżļ¤ē ļ░£ņāØĒĢ£ ĻĄ¼Ļ░äņØ┤ļŗż. ņØ┤ ļĢīņØś ļ»ĖņäĖņĪ░ņ¦üņØä ļ│┤ļ®┤, ņśżņŖżĒģīļéśņØ┤ĒŖĖņØś Ļ▓░ņĀĢļ”ĮĻ│ä ļ┐Éļ¦ī ņĢäļŗłļØ╝ ņŚ┤ ņīŹņĀĢļ”ĮĻ│ä ņŻ╝ļ│ĆņŚÉļÅä ņĢäĻ▓░ņĀĢņØ┤ ĒśĢņä▒ļÉ£ Ļ▓āņØä Ļ┤Ćņ░░ĒĢĀ ņłś ņ׳ļŗż (ĻĘĖļ”╝ 6b). ļśÉĒĢ£ ņĀäņ×ÉĒøäļ░®ņé░ļ×ĆĒÜīņĀłĻĖ░ļź╝ ĒÖ£ņÜ®ĒĢśņŚ¼ ĻĄ¼ ņśżņŖżĒģīļéśņØ┤ĒŖĖ Ļ▓░ņĀĢļ”ĮĻ│ä(Prior austenite grain boundary, PAGB)ļź╝ Ļ┤Ćņ░░ĒĢ£ Ļ▓░Ļ│╝ņØ┤ļŗż. ņ┤łĻĖ░ ĒÄśļØ╝ņØ┤ĒŖĖĻ░Ć ņāØņä▒ļÉ£ ņØ┤Ēøä, ņ¦ĆņåŹņĀüņØĖ ļ│ĆĒśĢņ£╝ļĪ£ ņØĖĒĢ┤ ļ¦ÄņØĆ ņĢäĻ▓░ņĀĢļ”ĮĻ│äĻ░Ć ļ░£ļŗ¼ĒĢ£ Ļ▓āņØä ņé┤ĒÄ┤ļ│╝ ņłś ņ׳ļŗż. Kernel average misorientation mapņØä ĒåĄĒĢ┤ ņĢäĻ▓░ņĀĢļ”ĮĻ│äņØś ĒśĢĒā£ņÖĆ Ēü¼ĻĖ░ ļČäĒż ļō▒ņØä ņĢī ņłś ņ׳ļŗż. ĒŖ╣Ē׳ ĻĘĖļ”╝ 6dņŚÉņä£ ĒÖöņé┤Ēæ£ļĪ£ Ēæ£ņŗ£ĒĢ£ ļČĆļČäņØś Ļ▓ĮņÜ░, ņŗ£ĒÄĖņØä ĻĖēļāē ņŗ£ĒéżĻĖ░ ņĀäņŚÉ ļ░£ļŗ¼ĒĢ£ ņĪ░ņ¦üņ£╝ļĪ£ ņĪ░ļīĆĒĢ£ ņĢäĻ▓░ņĀĢļ”ĮĻ│äĻ░Ć ļ░£ļŗ¼ļÉ£ Ļ▓āņØä ņĢī ņłś ņ׳ļŗż. ņØ┤ļŖö ņ¦ĆņåŹņĀüņØĖ ņåīņä▒ ļ│ĆĒśĢņ£╝ļĪ£ ņśżņŖżĒģīļéśņØ┤ĒŖĖņØś ļ░®ņ£äĻ░Ć 1ņČĢ ņĢĢņČĢņŚÉ ņ£Āļ”¼ĒĢ£ ļ░®Ē¢źņ£╝ļĪ£ ļ░öļĆīļŖö Ļ│╝ņĀĢņŚÉņä£ ņāłļĪŁĻ▓ī ļéśĒāĆļé£ ĒÄśļØ╝ņØ┤ĒŖĖļōżņØ┤ ĻĖ░ņĪ┤ņŚÉ ļéśĒāĆļé£ ĒÄśļØ╝ņØ┤ĒŖĖļōżĻ│╝ņØś ņŚ░ņåŹņä▒ņØä Ļ░¢ĻĖ░ ņ£äĒĢ┤ ļ░£ļŗ¼ļÉ£ Ļ▓āņ£╝ļĪ£ ņČöņĀĢļÉ£ļŗż. 1ņČĢ ņĢĢņČĢ ņØæļĀź ņāüĒā£ņŚÉņä£ ĒŖ╣ņĀĢ variantĻ░Ć ņäĀĒāØņĀüņ£╝ļĪ£ ļ░£ļŗ¼ļÉśļ®░ ĻĘĖņŚÉ ļīĆĒĢ£ ņŚÉļäłņ¦Ć Ļ┤ĆĻ│ä[25,26]ļŖö ņČöĒøä ļŗżļźĖ ņŚ░ĻĄ¼ ļģ╝ļ¼ĖņŚÉņä£ ĒåĀņØśĒĢĀ ņśłņĀĢņØ┤ļŗż.
ĻĘĖļ”╝ 7ņØĆ 1000ļÅäņÖĆ 600ļÅäņŚÉņä£ ņä£ļĪ£ ļŗżļźĖ ļ│ĆĒśĢņ£© ņåŹļÅäļź╝ ĒåĄĒĢ┤ ņ¢╗ņØĆ ļ│ĆĒśĢĻ▓ĮĒÖöņ£© Ļ░ÆņØä ļ╣äĻĄÉĒĢ£ Ļ▓āņØ┤ļŗż. ņØ╝ļ░śņĀüņ£╝ļĪ£ ļÅÖņĀü ņāüļ│ĆĒā£Ļ░Ć ļ░£ņāØĒĢśņ¦Ć ņĢŖļŖö ņĪ░Ļ▒┤ņŚÉņä£ ņśżņŖżĒģīļéśņØ┤ĒŖĖņØś ļÅÖņĀü ņ×¼Ļ▓░ņĀĢĻ│╝ ļÅÖņĀü ĒÜīļ│Ąļ¦ī ļéśĒāĆļéśļŖö Ļ▓ĮņÜ░, ņ”ē ļ│ĆĒśĢ ņś©ļÅäĻ░Ć ņČ®ļČäĒ׳ ļåÆņØĆ Ļ▓ĮņÜ░ņŚÉļŖö ĻĘĖļ”╝ 3ņŚÉņä£ ņäżļ¬ģĒĢ£ Ļ▓āņ▓śļ¤╝, ņäĖļĪ£ņČĢņ£╝ļĪ£ ņÖĖņéĮĒĢ£ Ļ░ÆņØ┤ ╬Ė0ņŚÉ ņłśļĀ┤ĒĢ£ļŗż (ĻĘĖļ”╝ 7a). ņØ┤ļŖö ĻĘĖļ”╝ 3Ļ│╝ ļ¦żņÜ░ ņ£Āņé¼ĒĢ£ ĒśĢĒā£ļĪ£ EstrinĻ│╝ MeckingĻ░Ć ņĀ£ņĢłĒĢ£ ļ¬©ļŹĖĻ│╝ ņØ╝ņ╣śĒĢ£ļŗż [5]. ļ░śļ®┤ņŚÉ ĻĘĖļ”╝ 7bņÖĆ Ļ░ÖņØ┤ ļ│ĆĒśĢ ņś©ļÅäĻ░Ć 600ļÅäņÖĆ Ļ░ÖņØ┤ ļé«ņØĆ Ļ▓ĮņÜ░ņŚÉļŖö, ļ│ĆĒśĢĻ▓ĮĒÖöņ£©ņØ┤ ļ│ĆĒśĢņ£© ņåŹļÅäņŚÉ ļö░ļØ╝ ĻĖēĻ▓®ĒĢśĻ▓ī ļ│ĆĒĢśļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. ņ”ē, ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć ļ╣ĀļźĖ Ļ▓ĮņÜ░ļ│┤ļŗż ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć ļŖÉļ”░ Ļ▓ĮņÜ░ņŚÉņä£ ņśżĒ׳ļĀż ļŹö ļåÆņØĆ ╬Ė ņĀłĒÄĖĻ░ÆņØä Ļ░¢ļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. ņØ┤ļŖö Zener-Hollomon ĒśäņāüĻ│╝ ņāüļ░śļÉśļŖö Ļ▓░Ļ│╝ļĪ£ ļŗ©ņØ╝ ņāüņØś ĒÜīļ│ĄņØ┤ ņĢäļŗī ļŗżļźĖ ņāüņ£╝ļĪ£ņØś ņāüļ│ĆĒā£ņŚÉ ņØśĒĢ┤ ļéśĒāĆļéśļ®░, ņØ┤ļź╝ ļ░öĒāĢņ£╝ļĪ£ ļÅÖņĀü ņāüļ│ĆĒā£ņØś ņ”ØĻ▒░ļĪ£ ņé╝ņØä ņłś ņ׳ļŗż. ņĢ×ņä£ ņäżļ¬ģĒĢśņśĆļō»ņØ┤ ļ│ĆĒśĢņØ┤ ņ▓£ņ▓£Ē׳ ņČ®ļČäĒĢ£ ņŗ£Ļ░äļÅÖņĢł ņØ╝ņ¢┤ļéśļ®┤ņä£ ļ│ĆĒśĢ ņżæ ļ░£ņāØļÉ£ ĒÄśļØ╝ņØ┤ĒŖĖļČäņ£©ņØ┤ ļ╣ĀļźĖ ļ│ĆĒśĢ ņåŹļÅäņØś Ļ▓ĮņÜ░ļ│┤ļŗż Ēü¼Ļ▓ī ņ”ØĻ░ĆļÉśĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ņ”ē, ĒÄśļØ╝ņØ┤ĒŖĖ ņāüĻ│╝ ņśżņŖżĒģīļéśņØ┤ĒŖĖ ņāüņØ┤ Ļ│ĄņĪ┤ĒĢśļ®┤ņä£, ņØ┤ņāü ņé¼ņØ┤ņØś ļ¦łņ░░ ņĀĆĒĢŁĻ│╝ ņ¦ĆņåŹņĀüņØĖ ĒÄśļØ╝ņØ┤ĒŖĖļĪ£ņØś ņāüļ│ĆĒā£, ĻĘĖļ”¼Ļ│Ā Ļ░ü ņāü ļé┤ļČĆņØś ņåīņä▒ ļ│ĆĒśĢĻ│╝ ņä£ļĪ£ ļŗżļźĖ ļÅÖņĀü ĒÜīļ│Ąņ£© ļō▒ņØś ļŗżņ¢æĒĢ£ ņøÉņØĖļōżņŚÉ ņØśĒĢ┤ ņĢ╝ĻĖ░ļÉ£ ņóģĒĢ®ņĀüņØĖ Ļ▓░Ļ│╝ņØ┤ļŗż. ņØ┤ļĀćĻ▓ī ņÖĖņéĮĒĢ£ ņ¦üņäĀļōżņØ┤ ĒĢśļéśņØś ņĀÉņØĖ ņ¦äņØæļĀź ņĢĮ 90 MPa ĻĘĖļ”¼Ļ│Ā ļ│ĆĒśĢĻ▓ĮĒÖöņ£© Ļ░ÆņØ┤ 1750 MPa ļČĆĻĘ╝ņŚÉņä£ ĻĄÉņ░©ĒĢśļŖö Ļ▓āņØä ļ░£Ļ▓¼ĒĢĀ ņłś ņ׳ļŗż. ņØ┤ Ļ░ÆņŚÉ Ļ┤ĆĒĢ£ ļ¼╝ļ”¼ņĀü ņØśļ»ĖņŚÉ ļīĆĒĢ┤ņä£ļŖö ņČöĒøä Ļ╣ŖņØ┤ Ļ│Āņ░░ĒĢĀ ĒĢäņÜöĻ░Ć ņ׳ļŗż.
ņĢ×ņäĀ ņŚ░ĻĄ¼ņŚÉņä£ ņĄ£ļīĆ ņ£ĀļÅÖ ņØæļĀźĻ░ÆņØä ĒÖ£ņÜ®ĒĢśņŚ¼ ņ¢╗ņØĆ ņ×äĻ│äņĀÉ(ZC)ņØä ņØ┤ņÜ®ĒĢ┤ ļÅÖņĀü ņāüļ│ĆĒā£ļź╝ ņśłņĖĪĒĢśļŖö Ļ▓ĮņÜ░, ņŗżĒŚś ņĪ░Ļ▒┤ņŚÉ ļö░ļØ╝ ņĄ£ļīĆ ņ£ĀļÅÖ ņØæļĀźņØä ņĀĢĒÖĢĒ׳ ņ¢╗ĻĖ░ ņ¢┤ļĀżņÜ┤ Ļ▓ĮņÜ░Ļ░Ć ļ¦ÄņØ┤ ļ░£ņāØĒĢĀ ņłś ņ׳ļŗż [18]. ņśłļź╝ ļōżļ®┤, ĻĘĖļ”╝ 1aņŚÉņä£ ļ│ĆĒśĢ ņś©ļÅäĻ░Ć ļé«ņØĆ Ļ▓ĮņÜ░, ņĄ£ļīĆ ņØæļĀźĻ░Æ ņäĀņĀĢ ņŗ£ ļ¦ÄņØĆ Ļ│Āļ»╝ņØ┤ ņÜöĻĄ¼ļÉ£ļŗż. ļśÉĒĢ£ ņĢ×ņäĀ ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņĄ£ļīĆ ņ£ĀļÅÖ ņØæļĀźņĀÉņØä ļÅÖņĀü ņŚ░ĒÖö ņżæ ĒĢśļéśņØĖ ņśżņŖżĒģīļéśņØ┤ĒŖĖņØś ļÅÖņĀü ņ×¼Ļ▓░ņĀĢ Ēś╣ņØĆ ļÅÖņĀü ņāüļ│ĆĒā£Ļ░Ć ĻĖēĻ▓®ĒĢśĻ▓ī ļ░£ņāØĒĢśĻĖ░ ņŗ£ņ×æĒĢśļŖö ņĀÉņ£╝ļĪ£ Ļ░äņŻ╝ĒĢśņśĆĻĖ░ ļĢīļ¼ĖņŚÉ, ņØ┤ļ»Ė ņŚ░ĒÖöĻ░Ć ĻĖēĻ▓®ĒĢśĻ▓ī ņŗ£ņ×æļÉ£ ņ×äĻ│äņĀÉņØĖ ņåīņä▒ ļČłņĢłņĀĢņĀÉ(critical point)ņØä Ļ░äĻ│╝ĒĢśņśĆļŗżļŖö ļ¼ĖņĀ£Ļ░Ć ņĀ£ĻĖ░ļÉśņŚłļŗż [18]. ĒĢśņ¦Ćļ¦ī ļ│Ė ņŚ░ĻĄ¼ ļģ╝ļ¼ĖņŚÉņä£ ņĀ£ņĢłĒĢ£ ļ░®ļ▓ĢņØä ĒåĄĒĢ┤, ļ│ĆĒśĢĻ▓ĮĒÖöņ£© ĻĖ░ņÜĖĻĖ░ņØś ļ│ĆĒÖöņØś ņåÉņē¼ņÜ┤ ņłśņ╣śĒĢ┤ņäØņĀüņØĖ ĻĖ░ļ▓Ģļ¦īņ£╝ļĪ£ ļÅÖņĀü ņāüļ│ĆĒā£ ņĪ░Ļ▒┤ņØä ņ¢╗ņØä ņłś ņ׳ļŖö ņןņĀÉņØ┤ ņ׳ļŗż. ļśÉ ļŗżļźĖ ņןņĀÉņ£╝ļĪ£ļŖö ņĄ£ļīĆ ņ£ĀļÅÖ ņØæļĀźĻ░Æļ│┤ļŗż Ēø©ņö¼ ļé«ņØĆ ņØæļĀźņ╣śļź╝ ņłśņ╣śļź╝ ĒÖ£ņÜ®ĒĢśņŚ¼ Ēś╣ņØĆ Ēø©ņö¼ ņĀüņØĆ ņ¢æņØś ņ¦äļ│ĆĒśĢņØä ņØ┤ņÜ®ĒĢśņŚ¼ ļÅÖņĀü ņāüļ│ĆĒā£ ļ░£ņāØ ņ£Āļ¼┤ļź╝ ņśłņĖĪĒĢĀ ņłś ņ׳ļŗż. ĻĘĖļ”╝ 7bņŚÉņä£ ļ│┤ļō»ņØ┤ ņ¦äņØæļĀźņØ┤ ņĢĮ 90 MPaņłśņżĆņŚÉņä£ ņÖĖņéĮ ņäĀļōżņØ┤ ĻĄÉņ░©ĒĢśļŖö Ļ▓āņØä ļ│╝ ņłś ņ׳ļŗż. ņśłļź╝ ļōżņ¢┤, ļ│ĆĒśĢņ£© ņåŹļÅäĻ░Ć 1.0 s-1ņØĖ Ļ▓ĮņÜ░, ļČłĻ│╝ 90 MPaņØ╝ ļĢīņØś ņ¦äļ│ĆĒśĢņØĆ 0.04 ņłśņżĆņ£╝ļĪ£ ņĄ£ļīĆ ņ£ĀļÅÖ ņØæļĀźņŚÉ ļīĆņØæļÉśļŖö ņ¦äļ│ĆĒśĢņØĖ 0.56ļ│┤ļŗż ļ¦żņÜ░ ņĀüņØĆ ļ│ĆĒśĢņ×äņØä ņĢī ņłś ņ׳ļŗż. ļ│ĆĒśĢļ¤ēņØ┤ ņĀüļŗżļŖö Ļ▓āņØĆ ņ¦¦ņØĆ ļ│ĆĒśĢ ņŗ£Ļ░äņØä ņØśļ»ĖĒĢśļ®░, ļé«ņØĆ ņ£ĀļÅÖņØæļĀź Ļ░ÆņØä ņØśļ»ĖĒĢ£ļŗż. ĒĢ┤ļŗ╣ ņĪ░Ļ▒┤ņŚÉņä£ļŖö ņØ┤ļ»Ė ļÅÖņĀü ĒÜīļ│Ąņ£©ņØ┤ ĻĖēĻ▓®Ē׳ ļé«ņĢäņ¦Ćļ®░, ļ│ĆĒśĢĻ▓ĮĒÖöņ£©Ļ░Ć ļ¦żņÜ░ ļåÆĻĖ░ ļĢīļ¼ĖņŚÉ ļÅÖņĀü ņāüļ│ĆĒā£ļź╝ ņ£äĒĢ£ ĻĄ¼ļÅÖļĀźņØä Ļ░Ćņ¦ł ņłś ņ׳ļŗż.
4. Ļ▓░ ļĪĀ
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ļŗżņ¢æĒĢ£ ļ│ĆĒśĢ ņś©ļÅäņÖĆ ļ│ĆĒśĢņ£© ņåŹļÅäļź╝ ĒåĄĒĢ┤ ņ¢╗ņØĆ ņ£ĀļÅÖ ņØæļĀź Ļ│ĪņäĀņØś ņĄ£Ļ│Ā ņØæļĀź Ļ░ÆņØä ņØ┤ņÜ®ĒĢ£ Zener-Hollomon Ļ┤ĆĻ│äņŗØņØä ņØ┤ņÜ®ĒĢ£ ņČöņĀü ļ░®ļ▓ĢņØ┤ ņĢäļŗī, ņĪ░Ļ▒┤ļ│ä ļ│ĆĒśĢĻ▓ĮĒÖöņ£©ņØä Estrin-Mecking ļ¬©ļŹĖņŚÉ ņĀüņÜ®ņŗ£ņ╝£ ļÅÖņĀü ņāüļ│ĆĒā£Ļ░Ć ļ░£ņāØĒĢśļŖö ņĀÉņØä ĒĢ┤ņäØĒĢśĻ│Āņ×É ĒĢśņśĆļŗż. ļÅÖņĀü ņŚ░ĒÖö ĒśäņāüņØĖ ņśżņŖżĒģīļéśņØ┤ĒŖĖņØś ļÅÖņĀü ņ×¼Ļ▓░ņĀĢņØ┤ ļ░£ņāØĒĢśļŖö ņĪ░Ļ▒┤ņØä ņ¢╗ņØĆ Ēøä, ņØ┤ļź╝ ļ░öĒāĢņ£╝ļĪ£ ņĢ×ņäĀ ĒĢ┤ņäØļ▓Ģļ│┤ļŗż ļŹöņÜ▒ ļ»╝Ļ░ÉĒĢśĻ▓ī ĒÄśļØ╝ņØ┤ĒŖĖļĪ£ņØś ļÅÖņĀü ņāüļ│ĆĒā£Ļ░Ć ļ░£ņāØĒĢśļŖö ņĪ░Ļ▒┤ņØä ļ░£Ļ▓¼ĒĢĀ ņłś ņ׳ņŚłļŗż. ĒŖ╣Ē׳ ļÅÖņĀü ĒÜīļ│ĄņØä ņĀ£ņÖĖĒĢ£ ļÅÖņĀü ņŚ░ĒÖö ņ×æņÜ®ņØ┤ ņŚåņØä Ļ▓āņ£╝ļĪ£ ņāØĻ░üĒ¢łļŹś ņ┤łĻĖ░ ļ│ĆĒśĢ ĻĄ¼Ļ░äņØś Ļ░ÆņØä Ļ░Ćņ¦ĆĻ│Ā ļČäņäØĒĢśņśĆņØīņŚÉļÅä ļČłĻĄ¼ĒĢśĻ│Ā ļ│ĆĒśĢĻ▓ĮĒÖöņ£© Ļ░ÆņØ┤ Ēü¼Ļ▓ī ļ│ĆĒĢśļŖö Ļ▓āņ£╝ļĪ£ ļ│┤ņĢśņØä ļĢī, Zener-Hollomon Ļ┤ĆĻ│äņŗØņØä ļ¦īņĪ▒ĒĢśļŖö ĒŖ╣ņĀĢ ļ│ĆĒśĢņ£© ņåŹļÅä ļ░Å ļ│ĆĒśĢ ņś©ļÅäņŚÉņä£ļŖö ļÅÖņĀü ņŚ░ĒÖö ņ×æņÜ®ņØĖ ļÅÖņĀü ĒÜīļ│Ą ļ░Å ļÅÖņĀü ņ×¼Ļ▓░ņĀĢ Ēśäņāüļ│┤ļŗżļŖö ļÅÖņĀü ņāüļ│ĆĒā£Ļ░Ć ņĪ░ĻĖ░ņŚÉ, ņ”ē ļ│ĆĒśĢļ¤ēņØ┤ ņĀüņØä ļĢīņŚÉļÅä, ļ░£ņāØĒĢĀ ņłś ņ׳ņØīņØä ņל ļ│┤ņŚ¼ņżĆļŗż. ņØ┤ļź╝ ĒåĄĒĢ┤ ļÅÖņĀü ņāüļ│ĆĒā£Ļ░Ć ļ░£ņāØĒĢśļŖö ļ│ĆĒśĢņ£© ņåŹļÅä ļ░Å ļ│ĆĒśĢ ņś©ļÅäņØś ņĪ░Ļ▒┤ņØä ņśłņĖĪĒĢĀ ņłś ņ׳ļŗż.